求lca（最近公共祖先）的各种方法

其实很早前就学了求lca的方法，但是当时没有总结归纳的习惯，现在再把这些总结一遍。

---

暴力往上跳

先把x,y跳到同一层，然后再同时往上跳，直到成了同一个点，显然这个点就是它们的lca。
时间复杂度最坏是树的深度，树成一条链时，就GG了。

#include
#include
#define fo(i, x, y) for(int i = x; i <= y; i ++)
using namespace std;

const int Maxn = 100005;
int n, x, y;
int final[Maxn], tot;
struct edge {
	int next, to;
}e[Maxn * 2];

int bz[Maxn], dep[Maxn], fa[Maxn];

void link(int x, int y) {
	e[++ tot].next = final[x], e[tot].to = y, final[x] = tot;
	e[++ tot].next = final[y], e[tot].to = x, final[y] = tot;
}

void dg(int x) {
	bz[x] = 1;
	for(int k = final[x]; k; k = e[k].next) {
		int y = e[k].to; if(bz[y]) continue;
		dep[y] = dep[x] + 1;
		fa[y] = x;
		dg(y);
	}
}

void Init() {
	scanf("%d", &n);
	fo(i, 1, n - 1) {
		scanf("%d %d", &x, &y);
		link(x, y);
	}
}

int Lca(int x, int y) {
	if(dep[x] < dep[y]) swap(x, y);
	while(dep[y] > dep[x]) y = fa[y];
	while(x != y) x = fa[x], y = fa[y];
	return x;
}

void Build() {
	dep[1] = 1; dg(1);
}

int main() {
	Init();
	Build();
	
	scanf("%d %d", &x, &y);
	printf("%d", Lca(x, y));
}

---

倍增跳法

维护每个点向上跳2^j层后是哪个点，这是一个倍增表，过程与Rmq类似（见标）。
假设有x,y（dep[x] < dep[y]）
先将y跳到x那儿。
然后开始二分逼近，不断逼近到lca下面那一个点，再往上一层就是lca了。

#include
#include
#define fo(i, x, y) for(int i = x; i <= y; i ++)
#define fd(i, x, y) for(int i = x; i >= y; i --)
using namespace std;

const int Maxn = 100005, Maxc = 16;
int n, x, y;
int final[Maxn], tot;
struct edge {
	int next, to;
}e[Maxn * 2];

int bz[Maxn], dep[Maxn], fa[Maxn];
int fj[Maxc + 1][Maxn];

void link(int x, int y) {
	e[++ tot].next = final[x], e[tot].to = y, final[x] = tot;
	e[++ tot].next = final[y], e[tot].to = x, final[y] = tot;
}

void dg(int x) {
	bz[x] = 1;
	for(int k = final[x]; k; k = e[k].next) {
		int y = e[k].to; if(bz[y]) continue;
		dep[y] = dep[x] + 1;
		fa[y] = x;
		dg(y);
	}
}

void Init() {
	scanf("%d", &n);
	fo(i, 1, n - 1) {
		scanf("%d %d", &x, &y);
		link(x, y);
	}
}

int Lca(int x, int y) {
	if(dep[x] > dep[y]) swap(x, y);
	fd(i, Maxc, 0) if(dep[fj[i][y]] >= dep[x]) y = fj[i][y];
	fd(i, Maxc, 0) if(fj[i][x] != fj[i][y]) x = fj[i][x], y = fj[i][y];
	return x == y ? x : fa[x];
}

void Build() {
	dep[1] = 1; dg(1);
	fo(i, 1, n) fj[0][i] = fa[i];
	fo(j, 1, Maxc) fo(i, 1, n) fj[j][i] = fj[j - 1][fj[j - 1][i]];
}

int main() {
	Init();
	Build();
	
	scanf("%d %d", &x, &y);
	printf("%d", Lca(x, y));
}

欧拉序+Rmq求lca

欧拉序：就是沿着树一直走，可以倒着走，途中经过所有点就是欧拉序。

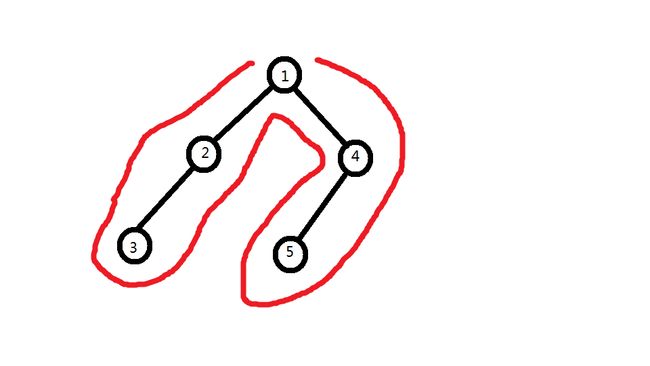
如图，它的欧拉序就是1-2-3-2-1-4-5-4-1

很显然，两个点的lca就是它们在欧拉序中的位置中间的深度最小的那个点，如果一个点在欧拉序中出现了多次，随便取一个即可。
欧拉序的长度不会超过点数的2倍，查询时O(1)的。

#include
#include
#include
#define fo(i, x, y) for(int i = x; i <= y; i ++)
#define fd(i, x, y) for(int i = x; i >= y; i --)
#define min(a, b) ((a) < (b) ? (a) : (b))
using namespace std;

const int Maxn = 100005, Maxc = 18;
int n, x, y;
int final[Maxn], tot;
struct edge {
	int next, to;
}e[Maxn * 2];

int bz[Maxn], dep[Maxn], fa[Maxn], d[Maxn * 2], dt[Maxn], d0;
int a2[Maxc + 1], fj[Maxc + 1][Maxn * 2];

void link(int x, int y) {
	e[++ tot].next = final[x], e[tot].to = y, final[x] = tot;
	e[++ tot].next = final[y], e[tot].to = x, final[y] = tot;
}

void dg(int x) {
	bz[x] = 1;
	d[++ d0] = x; dt[x] = d0;
	for(int k = final[x]; k; k = e[k].next) {
		int y = e[k].to; if(bz[y]) continue;
		dep[y] = dep[x] + 1;
		fa[y] = x;
		dg(y);
		d[++ d0] = x; dt[x] = d0;
	}
}

void Init() {
	scanf("%d", &n);
	fo(i, 1, n - 1) {
		scanf("%d %d", &x, &y);
		link(x, y);
	}
}

int Lca(int x, int y) {
	if(dt[x] > dt[y]) swap(x, y);
	int lg = log2(dt[y] - dt[x] + 1);
	return dep[fj[lg][dt[x]]] < dep[fj[lg][dt[y] - a2[lg] + 1]] ? fj[lg][dt[x]] : fj[lg][dt[y] - a2[lg] + 1];
}

void Build() {
	a2[0] = 1; fo(i, 1, Maxc) a2[i] = a2[i - 1] * 2;
	dep[1] = 1; dg(1);
	fo(i, 1, d0) fj[0][i] = d[i];
	fo(j, 1, Maxc) fo(i, 1, d0)
		fj[j][i] = dep[fj[j - 1][i]] < dep[fj[j - 1][min(d0, i + a2[j - 1])]] ? fj[j - 1][i] : fj[j - 1][min(d0, i + a2[j - 1])];
}

int main() {
	Init();
	Build();
	
	scanf("%d %d", &x, &y);
	printf("%d", Lca(x, y));
}

Tarjan

这是我会的唯一 一种线性算法，实际上，它的常数有点大，在小数据级跑得可能比以上的log算法还慢，OI一般也不会卡，但是确实出题人说他会线性算法的必备算法（比如GDOI2017）。
流程：
把各个询问打在两个点上。

递归，对于当前节点，先递归求子树内的lca
把挂在这个点上的询问一一处理，如果询问上的另一点已经遍历过，lca为另一点的并查集中的祖先。
把当前点在并查集中的父亲设为它在树上的父亲。
递归结束。

证明自己画个图搞搞吧。

#include
#include
#include
#define fo(i, x, y) for(int i = x; i <= y; i ++)
#define fd(i, x, y) for(int i = x; i >= y; i --)
#define min(a, b) ((a) < (b) ? (a) : (b))
using namespace std;

const int Maxn = 100005, Maxc = 18;
int n, x, y, Q, ans[Maxn], f[Maxn];
int final[Maxn], tot, final2[Maxn], tot2;
struct edge {
	int next, to, w;
}e[Maxn * 2], e2[Maxn * 2];

int bz[Maxn], dep[Maxn], fa[Maxn];

int find(int x) {
	return f[x] == x? x : (f[x] = find(f[x]));
}

void link(int x, int y) {
	e[++ tot].next = final[x], e[tot].to = y, final[x] = tot;
	e[++ tot].next = final[y], e[tot].to = x, final[y] = tot;
}

void link2(int x, int y, int z) {
	e2[++ tot2].next = final2[x], e2[tot2].to = y, e2[tot2].w = z, final2[x] = tot2;
	e2[++ tot2].next = final2[y], e2[tot2].to = x, e2[tot2].w = z, final2[y] = tot2;
}

void Init() {
	scanf("%d", &n);
	fo(i, 1, n - 1) {
		scanf("%d %d", &x, &y);
		link(x, y);
	}
}


void Build() {
	scanf("%d", &Q);
	fo(i, 1, Q) {
		scanf("%d %d", &x, &y);
		link2(x, y, i);
	}
	fo(i, 1, n) f[i] = i;
}

void dg(int x) {
	bz[x] = 1;
	for(int k = final[x]; k; k = e[k].next)
		if(!bz[e[k].to])
			dg(e[k].to), f[e[k].to] = x;
	for(int k = final2[x]; k; k = e2[k].next)
		if(bz[e2[k].to])
			ans[e2[k].w] = find(e2[k].to);		
}

int main() {
	Init();
	Build();
	dg(1);
	fo(i, 1, Q) printf("%d ", ans[i]);
}

---

轻重链剖分法

相信打过链剖的同学都会。

#include
#include
#include
#define fo(i, x, y) for(int i = x; i <= y; i ++)
#define fd(i, x, y) for(int i = x; i >= y; i --)
#define min(a, b) ((a) < (b) ? (a) : (b))
using namespace std;

const int Maxn = 100005;
int n, x, y, Q, ans[Maxn], f[Maxn];
int final[Maxn], tot;
struct edge {
	int next, to;
}e[Maxn * 2];

int bz[Maxn], dep[Maxn], fa[Maxn], siz[Maxn], son[Maxn], top[Maxn];

void link(int x, int y) {
	e[++ tot].next = final[x], e[tot].to = y, final[x] = tot;
	e[++ tot].next = final[y], e[tot].to = x, final[y] = tot;
}


void Init() {
	scanf("%d", &n);
	fo(i, 1, n - 1) {
		scanf("%d %d", &x, &y);
		link(x, y);
	}
}

void dg(int x) {
	bz[x] = 1;
	siz[x] = 1;
	for(int k = final[x]; k; k = e[k].next) {
		int y = e[k].to; if(bz[y]) continue;
		dep[y] = dep[x] + 1;
		fa[y] = x;
		dg(y);
		siz[x] += siz[y];
		if(siz[y] > siz[son[x]]) son[x] = y;
	}
	bz[x] = 0;
}

void dg2(int x) {
	bz[x] = 1;
	if(top[x] == 0) top[x] = x;
	if(son[x] != 0) top[son[x]] = top[x], dg2(son[x]);
	for(int k = final[x]; k; k = e[k].next) {
		int y = e[k].to; if(bz[y]) continue;
		dg2(y);
	}
}

int Lca(int x, int y) {
	while(top[x] != top[y])
		if(dep[top[x]] >= dep[top[y]]) x = fa[top[x]]; else y = fa[top[y]];
	return dep[x] < dep[y] ? x : y;
}

void End() {
	scanf("%d", &Q);
	fo(i, 1, Q) {
		scanf("%d %d", &x, &y);
		printf("%d ", Lca(x, y));
	}	
}

int main() {
	Init();
	dep[1] = 1; dg(1);
	dg2(1);
	
	End();
}

时间比对：

附1000000随机数据评测结果：

多个点的lca

就是一个点到其它所有点的lca的深度最小的那一个，感性证明。