数字图像处理 表示与描述( 部分)
- 表示与描述
- 背景知识
- 单元数组与结构
- 本章中使用的一些其他MATLAB和IPT函数
- 一些基本的M函数
- 表示
- 链码
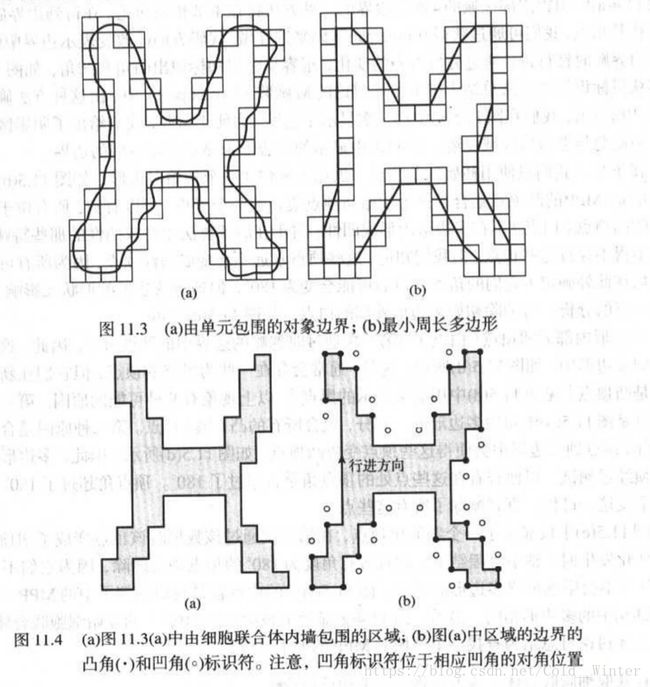
- 使用最小周长多边形的多边形近似
- 标记
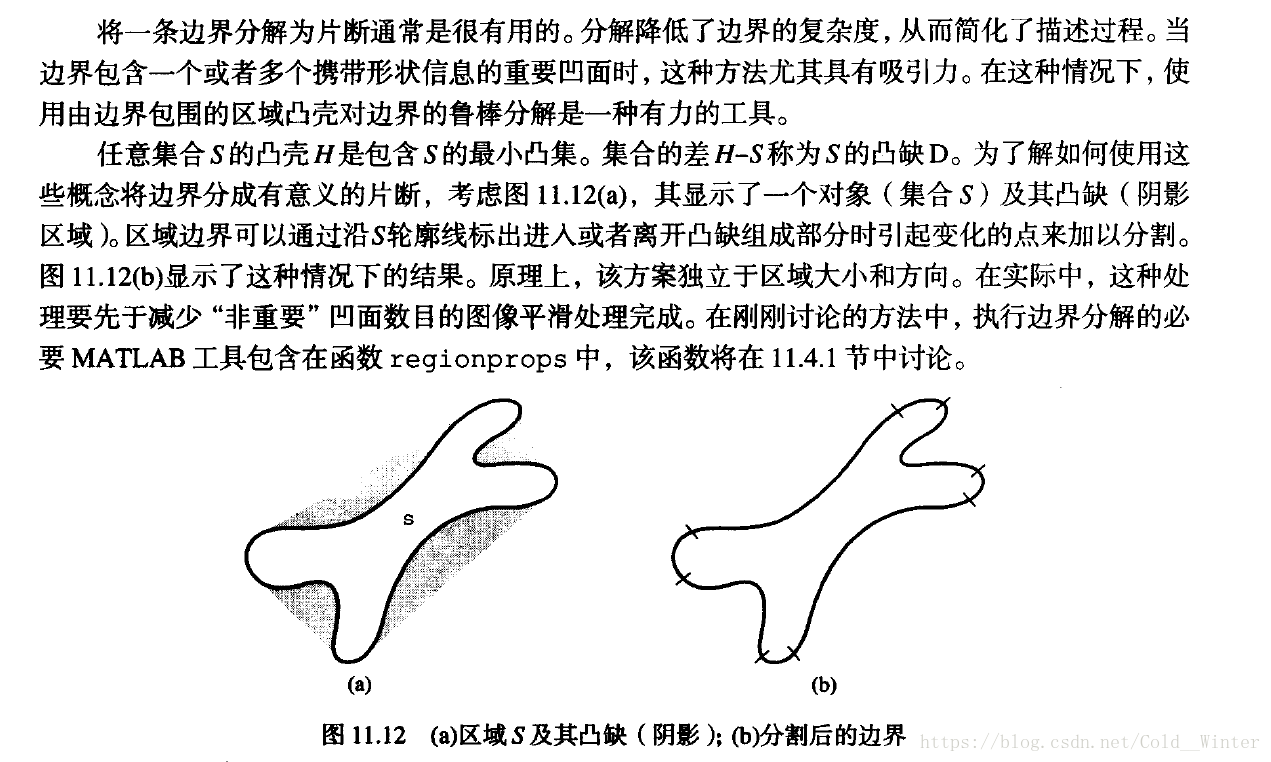
- 边界片段
- 骨骼
- 背景知识
表示与描述
背景知识
单元数组与结构
单元数组:
结构:
简单说明:
本章中使用的一些其他MATLAB和IPT函数
imfill:
对于二值图像:
gB = imfill(fB, locations, conn);在输入二值图像fB的背景像素上从参数locations指定的点开始,执行填充操作(即将背景像素值设为1)。
使用语法gB = imfill(fB, conn, 'holes');可填充用输入二值图像中的孔洞。
灰度图像:
g = imfill(fI, conn, 'holes');将填充输入灰度图像fI的孔洞。在这种情况中,孔洞是指较亮像素保卫的暗像素区域,参数conn如上所述。
find:
函数find 可以和bwlabel一起使用,还会构成某个指定对象的像素的坐标向量。
[r, c] = find(g == 2);sortrows:
本章中,区域或者边界的二维坐标被组织成np*2数组的形式,其中每行是一个(x,y)坐标对,np是区域或边界中的点的数目,某些情况下,有必要对数组进行排序。为此,可以使用函数sortrows
z = sortrows(s);该函数按升序对数组s的行进行排序。参量s必须是矩阵或者列向量。
unique:
若想对数组s的行排序,又要去除重复行,则可使用函数unique,其语法:
[z, m, n] = unique(S, 'rows');circshift:
通常,有必要对数组行进行向上,向下或者侧移指定位置数的移位操作,为此我们使用函数circshift:
z = circshift(S, [ud lr])一些基本的M函数
函数boundaries
B = boundaries(f, conn, dir);跟踪f中的对象的外部边界,f假设为一幅二值图像,其背景像素为0.参数conn指明输出边界的期望连接方式,其值可为4或8(默认)。
函数bound2im
g = bound2im = (b, M, N, x0, y0);生成一幅二值图像g,该图像的大小为M * N,边界点为1, 背景值为0.参数x0和y0决定图像中b的最小x和y坐标位置。边界b必须是坐标的一个大小为np*2的数组。
函数bsubsamp
[s, su] = bsubsamp(b,gridsep);在一个网格上对单一边界b二次取样,网格线由gridsep像素分离。输出s是一个比b有更少的点的边界,点的数目由gridsep的值决定,su是按比例取得的边界点的集合,这样可以使坐标的转换趋于一致。
表示
链码
函数fchcode的语法为
c = fchcode(b, conn, dir);Freeman链码:
>> f = imread('Fig1102(a)(noisy_circular_stroke).tif');
>> imshow(f),title('原图');
>> h = fspecial('average', 9);
>> g = imfilter(f, h ,'replicate');
>> figure,imshow(g),title('9*9掩模处理结果');
>> g = im2bw(g,0.5);
>> figure,imshow(g),title('阈值处理后结果');
>> B = boundaries(g);
>> d = cellfun('length',B);
>> [max_d, k] = max(d);
>> b = B{1};
>> [M N] = size(g);
>> g = bound2im(b,M,N,min(b(:,1)),min(b(:,2)));
>> figure,imshow(g);
>> [s,su] = bsubsamp(b,50);
>> g2 = bound2im(s,M,N,min(s(:,1)),min(s(:,2)));
>> figure,imshow(g2);
>> cn = connectpoly(s(:, 1), s(:, 2));
>> g2 = bound2im(cn,M,N,min(cn(:,1)),min(cn(:,2)));
>> figure,imshow(g2);4.边界
5. 边界二次取样
6. 将边界二次取样连接
使用最小周长多边形的多边形近似
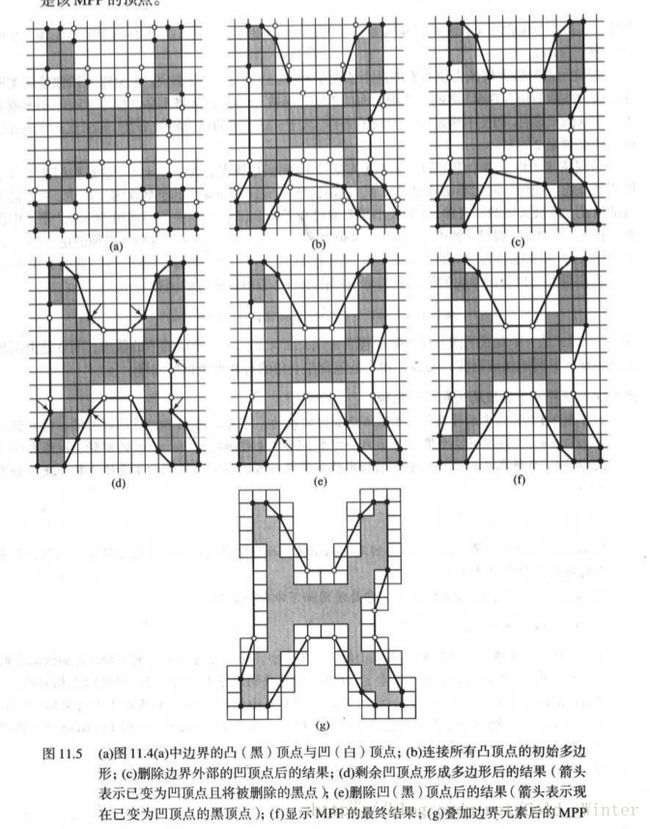
查找MPP的算法
计算MPP的函数
>> B = imread('Fig1107(a)(mapleleaf).tif');
>> b = boundaries(B,4,'cw');
>> b = b{1};
>> [M,N] = size(B);
>> xmin = min(b(:,1));
>> ymin = min(b(:,2));
>> bim = bound2im(b,M,N,xmin,ymin);
>> imshow(B);figure,imshow(bim);
>> [x,y] = minperpoly(B,2);
>> b2 = connectpoly(x,y);
>> B2 =bound2im(b2,M,N,xmin,ymin);
>> figure,imshow(B2);
>> [x,y] = minperpoly(B,3);
>> b3 = connectpoly(x,y);
>> B3 =bound2im(b3,M,N,xmin,ymin);
>> figure,imshow(B3);
>> [x,y] = minperpoly(B,4);
>> b4 = connectpoly(x,y);
>> B4 =bound2im(b4,M,N,xmin,ymin);
>> figure,imshow(B4);
>> [x,y] = minperpoly(B,8);
>> b8 = connectpoly(x,y);
>> B8 =bound2im(b8,M,N,xmin,ymin);
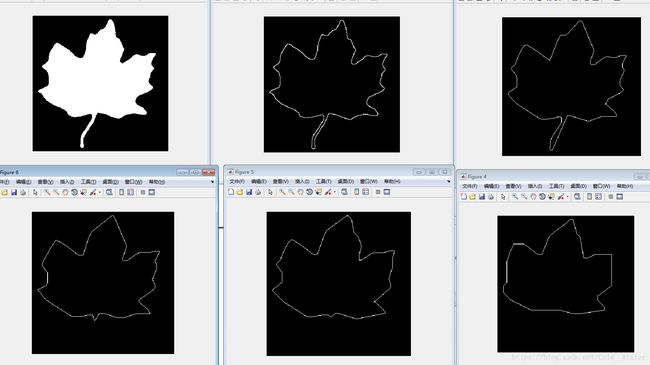
>> figure,imshow(B8);1原图
2 4连接边界
3使用大小为2的方形边界单元获得的MPP
4~6 分别使用大小为 3,4,8方形边界单元获得的MPP
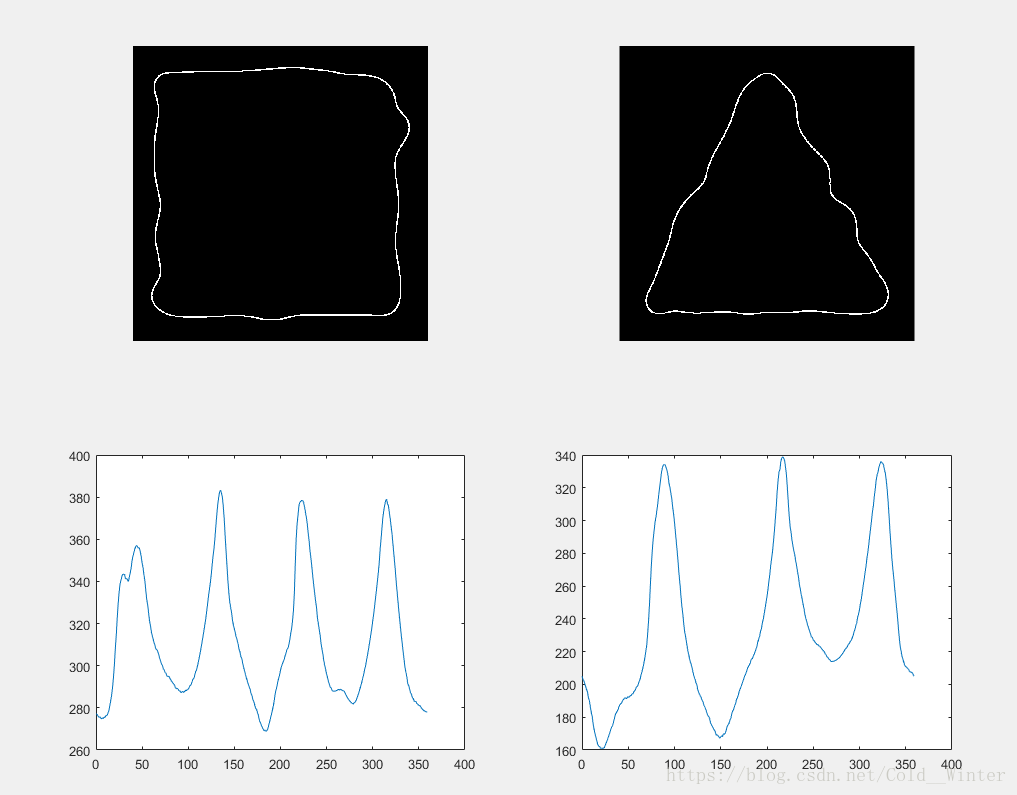
标记
>> f = imread('Fig1111(a)(boundary_sq.tif');
>> f = imdilate(f, ones(3, 3));
>> subplot(2, 2, 1), imshow(f);
>> B = boundaries(f, 4, 'cw');
>> d = cellfun('length', B);
>> [max_d, k] = max(d);
>> b = B{k(1)};
>> [st, angle, x0, y0] = signature(b);
>> subplot(2, 2, 3), plot(angle, st);
>>> g = imread('Fig1111(b)(boundary_triangle).tif');
>> g = imdilate(g, ones(3, 3));
>> subplot(2, 2, 2), imshow(g);
>> B = boundaries(g, 4, 'cw');
>> d = cellfun('length', B);
>> [max_d, k] = max(d);
>> b = B{k(1)};
>> [st, angle, x0, y0] = signature(b);
>> subplot(2, 2, 4), plot(angle, st);不规则方形与三角形边界以及相应标记
边界片段
骨骼
>> f = imread('Fig1113(a)(chromo_original).tif');
>> f = im2double(f);
>> h = fspecial('gaussian',25);
>> g = imfilter(f,h,'replicate');
>> imshow(f);
>> figure,imshow(g);
>> g = im2bw(g,1.5*graythresh(g));
>> figure,imshow(g);
>> s = bwmorph(g,'skel',Inf);
>> s1 = bwmorph(g,'spur',8);
>> s2 = bwmorph(g,'spur',7);
>> figure,imshow(s); figure,imshow(s1); figure,imshow(s2);
>> s1 = bwmorph(s,'spur',8);
>> s2 = bwmorph(s1,'spur',7);
>> figure,imshow(s); figure,imshow(s1); figure,imshow(s2);1原图
2使用25*25高斯空间掩模(sig=15)平滑图像f后的结果
3经阈值处理后的结果
4骨骼
5应用8次去除毛刺之后的骨骼
6再应用7次去除毛刺之后的骨骼