【日常练习】 消耗战【虚树】
传送门
前言
分块没有咕只是今天我懒得更 毕竟上周没上课不是
在学淀粉质的时候看到了动态淀粉质,然后发现需要学虚树,然后发现自己没写过虚树。
然后就有了这道题。
题目大意
一棵树,n个点,每条边有边权。k次询问,每次询问给出一些点,求让这些点都与根节点不连通所需要断开的边的价值之和的最小值。
题解
1、一次询问
那么首先可以看出这肯定是个树形DP。如果我们只有一次询问,这题就很简单了。
d p [ n ] dp[ n ] dp[n] 表示让以n为根节点的子树中所有特殊点与原树根节点不联通的最小代价。
l e a [ n ] lea[ n ] lea[n]表示从n到原树根节点上的边权最小值。
然后 d p [ n ] = ∑ m i n ( d p [ d ] , l e a [ d ] ) , d = s o n [ n ] dp[ n ]=\sum min( dp[d],lea[d] ),d=son[n] dp[n]=∑min(dp[d],lea[d]),d=son[n] .
这里多说几句(因为我看这方程一开始没看懂还以为是错的
我曾疑惑这个地方如果累加多次 l e a [ d ] lea[d] lea[d]会不会对答案产生影响,事实证明在递归处理到上一层的时候会自动去除掉这种不优的选择,因而答案的正确性有保证(所以我是多傻
2、多次询问
那么这题明显要求的是多次询问,我们要是直接做的话,每次DP复杂度 O ( N ) O(N) O(N),M次询问,emmm……
所以就考虑下优化:我们在DP的时候,那些不是特殊点的点只起到了传递信息的作用,对答案却没什么实际影响,那我们能不能跳过它们从而节约时间呢?还真能。
我们把那些无用的路径压缩一下,没有特殊点的子树丢掉,这棵树就会变成一棵只有特殊点,特殊点的LCA,以及根节点的树,比之前那棵要小很多。
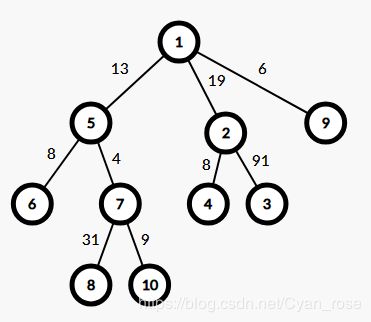
用样例1举例:
原树:
压缩后:
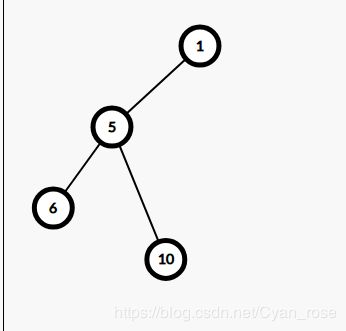
那么我们现在在这棵树上搞事情,就很简单啦~
好的这就是虚树的主要思想:把原树上的关键点提取出来,在另一颗更小的树上搞事情,以此减少时间。对于此题来说,复杂度可以下降到 O ( k l o g k ) O(klogk) O(klogk)
OK,既然知道要用虚树了,我们现在就来看看怎么构造虚树吧。
3、虚树相关操作
首先是前置工作。
对于构造一棵新的树这件事,你既可以重开节点重新连边,当然也可以通过欧拉序+手动模拟DFS搞定这种事。我反正觉得后者方便一点(免得我老眼昏花看错了
然后考虑到我们还需要找特殊点的LCA并加入到新树中(否则搜索顺序没法保证),所以我们还得要个求LCA的,当然你写树剖也可以,不过倍增常数小对吧~
所以第一步:搜索,处理欧拉序+倍增(基本操作就不多说了
ivoid get(int x,int fa)
{
par[x][0]=fa;
for(rint i=1;par[x][i-1];i++){
par[x][i]=par[par[x][i-1]][i-1];
}
}
ivoid dfs(int x,int fa)
{
in[x]=++num;
for(rint i=head[x];i;i=e[i].next){
int d=e[i].v;
if(d==fa)continue;
deep[d]=deep[x]+1;
lea[d]=min(lea[x],e[i].w);
get(d,x);dfs(d,x);
}out[x]=++num;
}
iint Lca_pos(int x,int y)
{
if(deep[x]!=deep[y]){
if(deep[x]<deep[y])swap(x,y);
for(rint i=20;i>=0;i--){
if(deep[par[x][i]]>=deep[y])
x=par[x][i];
}
}
if(x==y)return x;
for(rint i=20;i>=0;i--){
if(par[x][i]==par[y][i])continue;
x=par[x][i],y=par[y][i];
}
return par[x][0];
}
第二步:构造虚树。详情见代码。
m=rad();
while(m--){
x=rad();
for(rint i=1;i<=x;i++)a[i]=rad(),vis[a[i]]=1,dp[a[i]]=lea[a[i]];
//读入关键点,且标记访问过,顺便把dp也给弄了
sort(a+1,a+x+1,cmp);//
//然后先按着进入的欧拉序排个序
num=x;
for(rint i=1;i<x;i++){
int lc=Lca_pos(a[i],a[i+1]);
if(!vis[lc])vis[lc]=1,a[++num]=lc;
}
//建立虚树,加入个别的LCA
if(!vis[1])a[++num]=1;
//特判来加入一号点,要不然怎么搜
int num1=num;
for(rint i=1;i<=num1;i++)a[++num]=-a[i];
//然后建立各点的弹出点
sort(a+1,a+num+1,cmp);
//再以把进出顺序拿来排序
第三步:愉快的模拟DFS
r=0;
for(rint i=1;i<=num;i++){
if(a[i]>0)b[++r]=a[i];
else{
int now=b[r--];
if(now!=1)dp[b[r]]+=min(dp[now],(ll)lea[now]);
else cout<<dp[1]<<endll;
//dp请自行体会
dp[now]=0;vis[now]=0;
//这里让你可以循环利用
}
}
好的我们就这样愉快的解决了一个虚树题~
总结一下
这是我第一次写虚树的题,看得出来虚树受到的限制还是比较大的,比如当每个点的信息都会影响到最终答案时,虚树肯定就不能用了。
但是我不能否认虚树给我开拓了一条新的思路:在维护关键信息时,可以考虑用虚树来简化不必要的信息传递过程以此大幅降低时间和空间的复杂度。
总之就是这样了~