最大流算法——Dinic & 当前弧优化
洛谷博客地址:->Click Here<-,求捧场
不会写 E K EK EK的蒟蒻【我】哭出了声
所以来讲讲 D i n i c Dinic Dinic好了……
D i n i c Dinic Dinic的核心思想就是先跑一遍 B f s Bfs Bfs,为每个位置设置一个高度,一个点的高度为前一个点 + 1 +1 +1(如果某一条边已经满流则不设置)
在解释为什么要给图上的点设置高度,即设置所谓的分层图之前,我们先来讲讲网络流的建图方法
建边方法
虽然网络流的图看着是单向的,但我们在设置时应引入残流网络的概念,即对于每条边,都要设置一条反向的边,即原来的建图过程为:
AddEdge(from,to,flow);
现在为:
AddEdge(from,to,flow);
AddEdge(to,from,0);
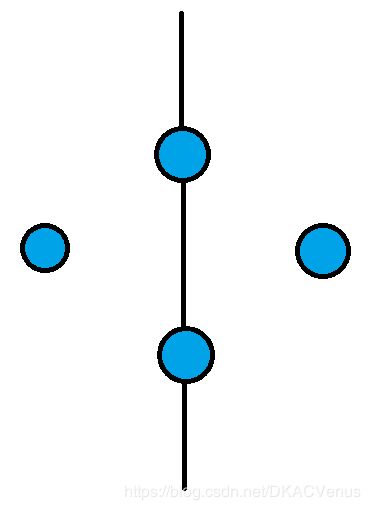
为什么要这么做呢?假设我们现在选择的增广路为下图(连的边未画出):
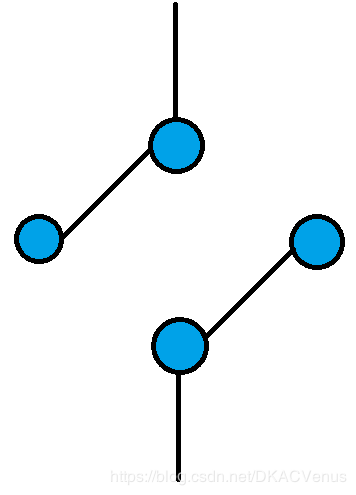
但它并不是最优的,而最优的如下:
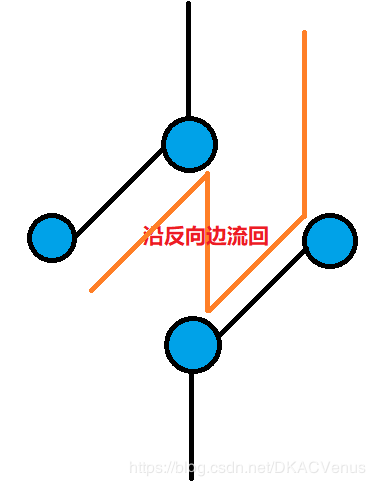
那这种方式就相当于:
这样就可以流确保选择最优的增广路了
分层图的设置
接下来我们讲为什么在 B f s Bfs Bfs的时候要设置高度,即为什么要设置分层图(炒鸡形象的名字),主要是为了加速整个算法的时间
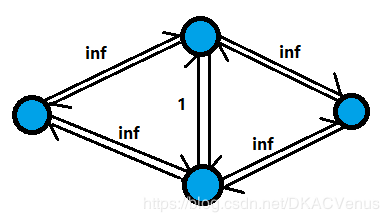
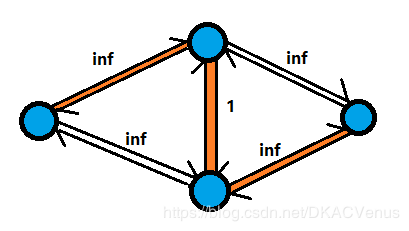
假设有这么一张图(左侧点为源点,右侧点为汇点):
我们在第一次找增广路时,虽然我们能一眼看出直接跑两条 i n f − > i n f inf->inf inf−>inf即可,但程序不一定会这么走,如果策略不对的话,第一次找到的增广路可能是这样的:
( i n f inf inf边的残量未标出)
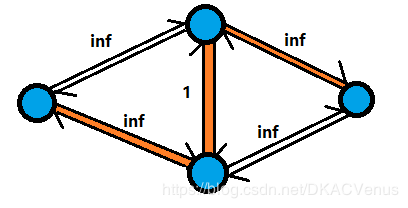
而下一次增广,找到的增广路可能是这样的:
这样一共会跑多少遍呢?是 i n f ∗ 2 inf*2 inf∗2遍,对于一个把 i n f inf inf设成 1010580540 1010580540 1010580540的人来说,这个复杂度是完全不能接受的
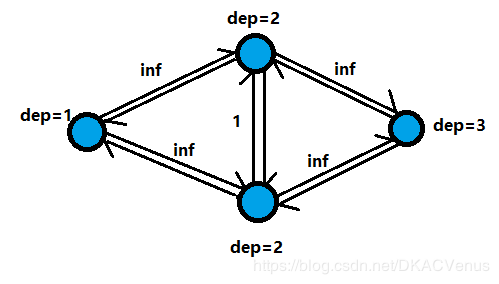
所以我们加入一个 B f s Bfs Bfs过程,在设置高度的同时能够确认这个网络还能不能跑到汇点
分层后的图如下:
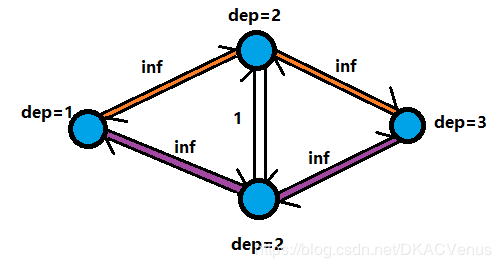
此时再找增广路,结果是这样的:
就可以很快地找到最优的方法了
D i n i c 模板 V 1.0 \text{\huge $Dinic$模板$V1.0$} Dinic模板V1.0
按照上面的要素,我们可以写出一个 D i n i c Dinic Dinic的板子
如下:
bool Bfs()//设置分层图
{
memset(dep,0,sizeof(dep));
q.push(S);
dep[S]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=fst[u];i;i=nxt[i])
{
int v=to[i];
if(!dep[v] && w[i])
{
dep[v]=dep[u]+1;//等于上一个加一
q.push(v);
}
}
}
return dep[T];//判断流能否到达汇点
}
int Dfs(int u,int flow)//寻找增广路
{
if(u==T || !flow) return flow;
int used=0;
for(int i=fst[u];i;i=nxt[i])
{
int v=to[i];
if(dep[v]==dep[u]+1 && w[i])
{
int fl=Dfs(v,min(flow,w[i]));
if(fl)
{
used+=fl;
flow-=fl;
w[i]-=fl;
w[i^1]+=fl;//残量网络处理
if(!flow) break;
}
}
}
return used;
}
int Dinic()
{
int sum=0;
while(Bfs()) sum+=Dfs(S,inf);//一直跑直到流无法到达汇点
return sum;
}
当前弧优化
我们知道,在寻找增广路的过程中,如果找到了,那么会直接先朝增广路流过去,一直流到汇点,在这个过程中,必然有一条边达到了满流,即流不能再经过这条边,那么我们找到的该条增广路也就不能跑了,但是在下一次增广的过程中,如果再次到达这个点,而找到了不能增广的路进行增广(因为第一次找到的增广路可能还有流量,而无法到达汇点),就会徒增很多的时间复杂度,所以我们引入一个数组 c u r [ ] cur[] cur[],记录每个点下一次该走的边(因为一个点可能有多条边可走,而在前面的一些边可能已经把当前流量花光,而且那些边也不再能增广,流量花光就直接退出了循环),这样就能省下不少的时间复杂度
D i n i c 模板 V 2.0 \text{\huge $Dinic$模板$V2.0$} Dinic模板V2.0
修改处在代码中标出
bool Bfs()
{
memset(dep,0,sizeof(dep));
q.push(S);
dep[S]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=fst[u];i;i=nxt[i])
{
int v=to[i];
if(!dep[v] && w[i])
{
dep[v]=dep[u]+1;
q.push(v);
}
}
}
return dep[T];
}
int Dfs(int u,int flow)
{
if(u==T || !flow) return flow;
int used=0;
for(int i=cur[u];i;i=nxt[i])
{
cur[u]=i;//标记下一次要走的边
int v=to[i];
if(dep[v]==dep[u]+1 && w[i])
{
int fl=Dfs(v,min(flow,w[i]));
if(fl)
{
used+=fl;
flow-=fl;
w[i]-=fl;
w[i^1]+=fl;
if(!flow) break;
}
}
}
return used;
}
int Dinic()
{
int sum=0;
while(Bfs())
{
memcpy(cur,fst,sizeof(fst));//每次重置cur数组
sum+=Dfs(S,inf);
}
return sum;
}
欢迎找 B u g Bug Bug
F i n . Fin. Fin.