边分治以及一些树上毒瘤题

边分治

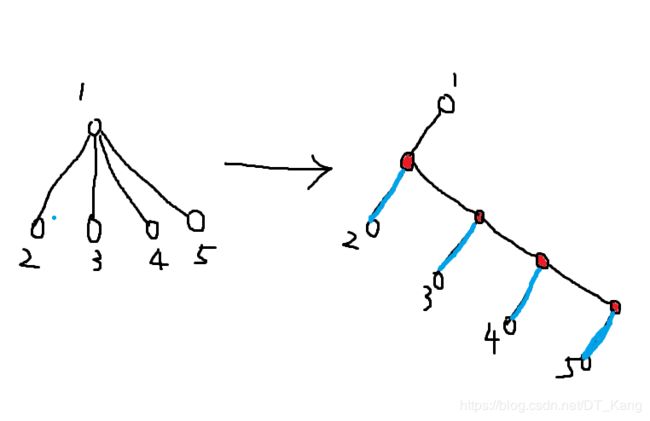
多叉树转二叉树

红色节点为虚点，一般储存父亲的点权信息（如本题）。

蓝边为实边，也就是原来的边。

void Insert(int u,int v)
{
	tot++;
	a[tot]=a[ind[u]];
	add_edge(tot,v,1);
	add_edge(v,tot,1);
	add_edge(ind[u],tot,0);
	add_edge(tot,ind[u],0);
	ind[u]=tot;
}
void dfs0(int u,int ff)
{
	for(int j=0;j

流程

首先多叉树转二叉树，否则会被菊花图卡掉。

每次找到一条边尽可能平均地把树划分成两半。处理过这条边的信息。需要注意的是，由于只统计实点的答案，可能存在一种特殊情况：有距离为k的点，却没有距离为k-1的点。注意特判。

相比较点分的优势是每次只合并两个子树。劣势是不好处理有关点权和的信息。（因为转二叉以后lca的点权会丢失）

---

毒瘤题

1

BZOJ2870
给定一棵N个点的树，求树上一条链使得链的长度乘链上所有点中的最小权值所得的积最大。其中链长度定义为链上点的个数。

链上点个数等于经过的实边+1。在一层点分里用双指针扫一遍即可。根据前面提到的注意事项，随着深度的增大，某一深度到根的最小值不一定单调。注意特判。

#include
#define ll long long
using namespace std;
const int N=200010;
struct edge{
	int to,next,w;
}ed[N<<1];
int ind[N],size[N],res,a[N],aa[N],bb[N],cnt1,cnt2,tot,n,sz=1,head[N],cut[N<<1],totsize,nowmin;
ll ans=0;
vector  b[N];
inline void add_edge(int from,int to,int w)
{
	ed[++sz].to=to;
	ed[sz].next=head[from];
	ed[sz].w=w;
	head[from]=sz;
}
inline int read()
{
	char c=getchar();int x=0,flag=1;
	while(!isdigit(c)){if(c=='-') flag=-1;c=getchar();}
	while(isdigit(c)) x=x*10+c-'0',c=getchar();
	return x*flag;
}
void Insert(int u,int v)
{
	tot++;
	a[tot]=a[ind[u]];
	add_edge(tot,v,1);
	add_edge(v,tot,1);
	add_edge(ind[u],tot,0);
	add_edge(tot,ind[u],0);
	ind[u]=tot;
}
void dfs0(int u,int ff)
{
	for(int j=0;j=aa[i]||bb[p]==-1)) p++;
		if(bb[p-1]>=aa[i]) ans=max(ans,1ll*(p+i-2+ed[res].w)*aa[i]);        //notice!
	}
	p=1;
	for(int i=1;i<=cnt2;i++)
	{
		if(bb[i]==-1) continue;
		while(p<=cnt1&&(aa[p]>=bb[i]||aa[p]==-1)) p++;
		if(aa[p-1]>=bb[i]) ans=max(ans,1ll*(p+i-2+ed[res].w)*bb[i]);
	}
	solve(ss);
	solve(tt);
}
int main()
{
	n=tot=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=n;i++) if(a[i]<0) return 0;
	for(int i=1;i

2

WC2018 通道
给定三棵树，求 ${\max }_{x,y}\{dis1(x,y)+dis2(x,y)+dis3(x,y)\}$

首先，边分第一棵树¹。只处理跨子树的点对。如果我们把两棵子树里的点分别染成黑色和白色，那么我们只需要统计黑色到白色贡献。设本层边分边为 $(ss,tt)$，这样的一对点在第一棵树上的距离为 $dis1(x,ss)+dis1(y,tt)+val$。

把这些点拿到第二棵树上建虚树。发现我们可以枚举点对在第二棵树上的 Lca。这样一对点的答案就变成了 $dis1(x,ss)+dis1(y,tt)+val+deep2[x]+deep2[y]-2\cdot deep2[Lca2(x,y)]+dis3(x,y)$。除去常数项就是 $dis1(x,ss)+dis1(y,tt)+deep2[x]+deep2[y]+dis3(x,y)$。令 $w[x]=dis1(x,ss/tt)+deep2[x]$，原式可化为： $w[x]+w[y]+dis3(x,y)$。

想象在第三棵树上的每个点 $x$ 的下面挂一个 $x^{\prime }$，边权为 $w[x]$，那么我们要求的式子相当于 $dis3(x^{\prime },y^{\prime })$。

回顾一下，我们现在要对于第二棵树上的虚树上的每一个点，求出以它为 Lca 的点对在第三棵树上的最远距离。

有这样一个结论：如果一棵树的边权非负，那么两个点集并的最远点对的端点一定是原来两个点集最远点对中的两个。因此可以直接在虚树上合并。

就做完了:(
复杂度 $O(n{\log }^{2}n)$

（封装好东西）

#include
#define ll long long
using namespace std;
const int N=400010;
int n,cut[N],cnt,a[N],vis[N];
ll w[N],ans,ksj;
inline int read()
{
	char c=getchar();int x=0,flag=1;
	while(!isdigit(c)){if(c=='-') flag=-1;c=getchar();}
	while(isdigit(c)) x=x*10+c-'0',c=getchar();
	return x*flag;
}
namespace T3
{
	struct edge{
		int to,next;ll w;
	}ed[N<<1];
	
	int sz,head[N],deep[N],f[N<<1][19],tim,seq[N],dfn[N],gg[N<<1];
	ll sum[N];
	
	void add_edge(int from,int to,ll w)
	{
		ed[++sz].to=to,ed[sz].next=head[from];
		ed[sz].w=w,head[from]=sz;
	}
	void dfs0(int u,int ff)
	{
		seq[++tim]=u;
		dfn[u]=tim;
		deep[u]=deep[ff]+1;
		for(int i=head[u];i;i=ed[i].next)
		{
			int v=ed[i].to;
			if(v==ff) continue;
			sum[v]=sum[u]+ed[i].w;
			dfs0(v,u);
			seq[++tim]=u;
		}
	}
	int Lca(int x,int y)
	{
		x=dfn[x],y=dfn[y];
		if(x>y) swap(x,y);
		int k=gg[y-x+1];
		if(deep[f[x][k]]<=deep[f[y-(1<>1]+1;
		for(int i=1;i<=tim;i++) f[i][0]=seq[i];
		for(int j=1;j<=18;j++)
		{
			for(int i=1;i+(1<d) d=tmp,ss=a.ss,tt=a.tt;
		if((tmp=dis(b.ss,b.tt))>d) d=tmp,ss=b.ss,tt=b.tt;
		
		if((tmp=dis(a.ss,b.tt))>d) d=tmp,ss=a.ss,tt=b.tt;
		if((tmp=dis(b.ss,a.tt))>d) d=tmp,ss=b.ss,tt=a.tt;
		
		if((tmp=dis(a.ss,b.ss))>d) d=tmp,ss=a.ss,tt=b.ss;
		if((tmp=dis(a.tt,b.tt))>d) d=tmp,ss=a.tt,tt=b.tt;
		return (node){ss,tt};
	}
	
	void check(node a,node b,ll k)
	{
		if(a.ss==-1||b.ss==-1) return;
		ans=max(ans,dis(a.ss,b.ss)-(k<<1));
		ans=max(ans,dis(a.ss,b.tt)-(k<<1));
		ans=max(ans,dis(a.tt,b.ss)-(k<<1));
		ans=max(ans,dis(a.tt,b.tt)-(k<<1));
	}
	
	void add_edge(int from,int to,ll w)
	{
		ed[++sz].to=to,ed[sz].next=head[from];
		ed[sz].w=w,head[from]=sz;
	}
	void add_edge2(int from,int to,ll w)
	{
		ed2[++sz2].to=to,ed2[sz2].next=head2[from];
		ed2[sz2].w=w,head2[from]=sz2;
	}
	void dfs0(int u,int ff)
	{
		seq[++tim]=u;
		dfn[u]=tim;
		deep[u]=deep[ff]+1;
		A[u]=dfn[u];
		for(int i=head[u];i;i=ed[i].next)
		{
			int v=ed[i].to;
			if(v==ff) continue;
			sum[v]=sum[u]+ed[i].w;
			dfs0(v,u);
			seq[++tim]=u;
		}
		B[u]=tim;
	}
	int Lca(int x,int y)
	{
		x=dfn[x],y=dfn[y];
		if(x>y) swap(x,y);
		int k=gg[y-x+1];
		if(deep[f[x][k]]<=deep[f[y-(1<>1]+1;
		for(int i=1;i<=tim;i++) f[i][0]=seq[i];
		for(int j=1;j<=18;j++)
		{
			for(int i=1;i+(1<B[st[top]])) top--;
			add_edge2(st[top],a[i],0);
			st[++top]=a[i];
		}
	}
	void dp(int u)
	{
	//	cout< b[N];
	vector  c[N];
	void add_edge(int from,int to,ll w)
	{
		ed[++sz].to=to,ed[sz].next=head[from];
		ed[sz].w=w,head[from]=sz;
	}
	void Insert(int u,int v,ll w)
	{
		tot++;
		add_edge(tot,v,w);
		add_edge(v,tot,w);
		add_edge(ind[u],tot,0);
		add_edge(tot,ind[u],0);
		ind[u]=tot;
	}
	void dfs0(int u,int ff)
	{
		for(int j=0;j

3

CTSC2018 暴力写挂
给定两棵树（边权有负），定义两点间距离为 $deep1[x]+deep1[y]-deep1[Lca1(x,y)]-deep2[Lca2(x,y)]$。求两点间最大距离。

发现 $deep1[x]+deep1[y]-deep1[Lca1(x,y)]=(deep1[x]+deep1[y]+dis1(x,y))/2$。因此我们枚举第二棵树上的 $Lca$。注意到边权有负，因此不能简单维护点集最远点。一个想法是边分树维护一个第二棵树子树点集的信息，支持查询一个点到这个点集的最远距离。合并子树的时候启发式合并。这样是 $O(n{\log }^{2}n)$ 的。

观察到边分树是二叉树，与线段树类似，我们也可以对边分树进行合并，复杂度为 $O(n\log n)$。

构建边分树：

int solve(int u,int ff)
	{
		getsize(u,0);
		if(size[u]==1) return 0;
		totsize=size[u],nowmin=1e9;
		getedge(u,0);
		cut[res]=cut[res^1]=1;
		int ss=ed[res].to,tt=ed[res^1].to;
		val[res]=val[res^1]=ed[res].w;
		fa[res]=ff;
		bel[ss]=bel[tt]=res;
		int tmp=res;								//记得存tmp，否则递归会改变res
		son[tmp][0]=solve(ss,tmp);
		son[tmp][1]=solve(tt,tmp);
		return tmp;
	}

完整代码：

#include
#define ll long long
using namespace std;
const int N=366666*2+10;
int n,cnt,tot,pos[N*18],bel[N],gg[N<<1],ch[N*18][2],val[N<<1];
ll Max[N*18][2],ans=-1e18;
inline int read()
{
	char c=getchar();int x=0,flag=1;
	while(!isdigit(c)){if(c=='-') flag=-1;c=getchar();}
	while(isdigit(c)) x=x*10+c-'0',c=getchar();
	return x*flag;
}
namespace T1
{
	struct edge{
		int to,next,w;
	}ed[N<<1];
	
	int head[N],sz=1,son[N<<1][2],ind[N],deep[N],f[N<<1][21],tim,seq[N<<1],dfn[N],size[N],totsize,nowmin,res,fa[N<<1],cut[N<<1];
	ll sum[N];
	vector  b[N],c[N];
	
	inline void add_edge(int from,int to,int w)
	{
		ed[++sz].to=to;
		ed[sz].w=w;
		ed[sz].next=head[from];
		head[from]=sz;
		val[sz]=w;
	}
	void Insert(int u,int v,int w)
	{
		tot++;
		add_edge(tot,v,w);
		add_edge(v,tot,w);
		add_edge(ind[u],tot,0);
		add_edge(tot,ind[u],0);
		ind[u]=tot;
	}
	void dfs0(int u,int ff)
	{
		for(int j=0;jy) swap(x,y);
		int k=gg[y-x+1];
		if(deep[f[x][k]]<=deep[f[y-(1<>1]+1;
	T1::init(),T2::init();
	T1::solve(1,0);
	T2::dfs(1,0);
	cout<

4

给定两棵树，求 $\sum \min (dis1(x,y),dis2(x,y))$

口胡一下…

边分第一棵树，染上色，把点集在第二棵树上建虚树。

好像还不是很好搞… 我们边分虚树，统计的就变成了跨过虚树上这条边的黑白点对的贡献。

我们枚举黑色点，统计对面有多少个白色点，在第二棵树上的距离小于第一棵树上的距离。也就是
$$dis2(ss2,x)+dis2(tt2,y)+val2-dis1(ss1,x)-dis1(tt1,y)-val1<0$$

令 $w[x]=dis2(ss2,x)-dis1(ss1,x)$，可化简为：
$$w[x]+w[y]<val1-val2$$

对于一个 $x$，求出合法 $y$ 的数量，乘上 $dis2(ss2,x)$ 贡献进答案。其他的 $y$ 对应的就是 $dis1(ss1,x)$，同样贡献进答案。

还需要一个树状数组维护 $w$，复杂度 $O(n{\log }^{3}n)$。

---

1. 为什么不能点分？因为我们要对点进行黑白染色。这就是边分的优势：只需处理两个子树之间的贡献。当然也可以强行三度化以后点分，乘上3的常数:) ↩︎