多元回归分析python实战-----对我国财政收入的多因素进行分析
目录
前言
数据
python相关分析
分析结果
python回归分析
模型建立
模型检验
确定公式
分析结果
前言
财政收入的规模大小对一个国家来说具有十分重要的意义,本文章分别从财政收入的组成因素和财政收入的影响因素两个方面入手,对祖国1979-1999年度财政收入情况进行多因素分析。在财政收入影响因素分析上,除了通过理论选出因素并利用统计软件建立模型分析,还把影响财政收入的结构因素进行了个别分析,最后在分析结论的基础上,结合当前客观条件和政策因素对未来财政收入做了一定的期望。
数据
数据来自网络,一共含有9个因素,GDP、能源消费总量、从业人员总数、全社会固定资产投资总额、实际利用外资总额,全国城乡居民储蓄存款年底月、居民人均消费水平、消费品零售总额和居民消费价格指数。数据如下。
其中t: 年份;y:财政收入;x1:GDP;x2:能源消费总量;x3:从业人员总数;x4:全社会固定资产投资总额;x5:实际利用外资总额;x6:全国城乡居民储蓄存款年底月;x7:居民人均消费水平;x8:消费品零售总额;x9:居民消费价格指数
t y x1 x2 x3 x4 x5 x6 x7 x8 x9
1979 1146.38 4038.2 58558 41024 849.36 31.14 281 197 1800 102
1980 1139.53 4517.8 60237 42361 910.9 31.14 399.5 236 2140 108.1
1981 1173.79 4860.3 59447 43725 961 31.14 523.7 249 2350 110.7
1982 1212.33 5301.8 62067 45296 1230.4 31.14 675.4 266 2570 112.8
1983 1366.95 5937.4 65040 46436 1430.1 19.81 892.5 289 2849.4 114.5
1984 1642.86 7206.7 70904 48197 1832.9 27.03 1214.7 327 3376.4 117.7
1985 2004.82 8986.1 76501 49873 2543.2 46.47 1622.6 437 4305 128.1
1986 2122.04 10201.4 80850 51282 3120.5 72.58 2238.5 452 4950 135.8
1987 2199.35 11954.5 86632 52783 3791.7 84.32 3081.4 550 5820 145.7
1988 2357.24 11922.3 92997 54334 4763.8 102.26 3822.2 692 7440 172.7
1989 2664.9 16917.8 96934 55329 4410.4 100.39 5196.4 762 8101.4 203.4
1990 2937.1 18398.4 95703 63909 4517 102.89 7119.8 802 8300.1 207.7
1991 3149.48 21662.3 103783 64799 5594.3 113.54 9241.6 896 9415.6 213.7
1992 3483.37 26651.9 109170 65554 8080.1 192.02 11759.4 1070 10993.7 225.2
1993 4348.93 34360.5 113993 66373 13072.3 359.6 15203.5 1331 12462.1 254.9
1994 5158.1 46670 122737 67199 17042.1 432.13 21318.8 1746 16264.7 310.2
1995 6242.2 57494.9 131176 67947 20019.3 481.33 29662.3 2236 20620 356.1
1996 7407.99 66830.3 138946 68850 22913.5 548.04 38520.8 2641 24774.1 377.8
1997 9651.14 73142.7 138173 69500 24914.1 644.08 46279.8 2834 27298.9 380.5
1998 9875.95 76967.1 132214 69957 28406.2 585.57 53407.5 2972 29153.5 370.9
1999 11444.05 80422.8 122000 70586 29834.7 526.59 59621.8 3143 31134.7 359.8
python相关分析
导入数据
>>> import pandas as pd
>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>> from sklearn.linear_model import LinearRegression
>>> data = pd.read_csv('D:\python\DataAnalysis\data\Revenue.csv')
>>> pd.read_csv('D:\python\DataAnalysis\data\Revenue.csv')
t y x1 x2 ... x6 x7 x8 x9
0 1979 1146.38 4038.2 58558 ... 281.0 197 1800.0 102.0
1 1980 1139.53 4517.8 60237 ... 399.5 236 2140.0 108.1
2 1981 1173.79 4860.3 59447 ... 523.7 249 2350.0 110.7
3 1982 1212.33 5301.8 62067 ... 675.4 266 2570.0 112.8
4 1983 1366.95 5937.4 65040 ... 892.5 289 2849.4 114.5
5 1984 1642.86 7206.7 70904 ... 1214.7 327 3376.4 117.7
6 1985 2004.82 8986.1 76501 ... 1622.6 437 4305.0 128.1
7 1986 2122.04 10201.4 80850 ... 2238.5 452 4950.0 135.8
8 1987 2199.35 11954.5 86632 ... 3081.4 550 5820.0 145.7
9 1988 2357.24 11922.3 92997 ... 3822.2 692 7440.0 172.7
10 1989 2664.90 16917.8 96934 ... 5196.4 762 8101.4 203.4
11 1990 2937.10 18398.4 95703 ... 7119.8 802 8300.1 207.7
12 1991 3149.48 21662.3 103783 ... 9241.6 896 9415.6 213.7
13 1992 3483.37 26651.9 109170 ... 11759.4 1070 10993.7 225.2
14 1993 4348.93 34360.5 113993 ... 15203.5 1331 12462.1 254.9
15 1994 5158.10 46670.0 122737 ... 21318.8 1746 16264.7 310.2
16 1995 6242.20 57494.9 131176 ... 29662.3 2236 20620.0 356.1
17 1996 7407.99 66830.3 138946 ... 38520.8 2641 24774.1 377.8
18 1997 9651.14 73142.7 138173 ... 46279.8 2834 27298.9 380.5
19 1998 9875.95 76967.1 132214 ... 53407.5 2972 29153.5 370.9
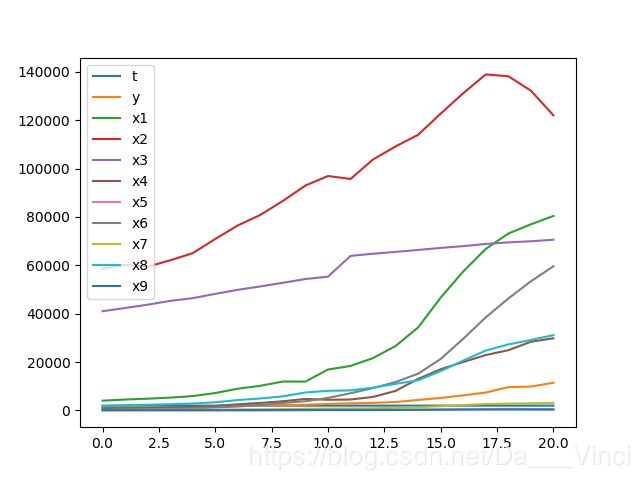
20 1999 11444.05 80422.8 122000 ... 59621.8 3143 31134.7 359.8>>> data.plot()相关系数矩阵
>>> print (data.corr())
t y x1 ... x7 x8 x9
t 1.000000 0.901941 0.920798 ... 0.924618 0.930975 0.955969
y 0.901941 1.000000 0.985051 ... 0.986643 0.990883 0.934222
x1 0.920798 0.985051 1.000000 ... 0.998871 0.996276 0.974196
x2 0.975170 0.862568 0.910217 ... 0.912941 0.911467 0.971141
x3 0.979701 0.829253 0.862643 ... 0.863775 0.868514 0.926190
x4 0.910709 0.984607 0.996498 ... 0.995362 0.992484 0.962281
x5 0.902074 0.946547 0.980987 ... 0.977137 0.967684 0.973785
x6 0.874597 0.995125 0.984902 ... 0.985560 0.987829 0.925630
x7 0.924618 0.986643 0.998871 ... 1.000000 0.998598 0.974454
x8 0.930975 0.990883 0.996276 ... 0.998598 1.000000 0.969709
x9 0.955969 0.934222 0.974196 ... 0.974454 0.969709 1.000000计算财政收入与其他列的相关系数
>>> print (data.corr()['y'])
t 0.901941
y 1.000000
x1 0.985051
x2 0.862568
x3 0.829253
x4 0.984607
x5 0.946547
x6 0.995125
x7 0.986643
x8 0.990883
x9 0.934222
Name: y, dtype: float64分析结果
根据相关系数,y与x1-x9的关系都非常密切(r > 0.8,ρ < 0.001),财政收入与城乡居民储蓄存款年底余额之间关系最为密切(r = 0.995,ρ < 0.001)
相关系数表明了各变量与财政收入之间的线性关系程度相当高,由此可以认为所选取的九个因素都与财政收入存在着线性关系。
基于此结果,觉的继续进行线性回归分析,以便建立财政收入与每个因素之间的回归模型。这里以财政收入为因变量,其他为自变量
python回归分析
这里我们使用了sklearn库,和高大上机器学习相关的
模型建立
>>> lrModel = LinearRegression()
>>> y = data['y'].values.reshape(-1, 1)
>>> x = data.ix[:,2:]这里因为函数的特殊性,即使是一维数组也要转换为二位数组。
>>> x
x1 x2 x3 x4 ... x6 x7 x8 x9
0 4038.2 58558 41024 849.36 ... 281.0 197 1800.0 102.0
1 4517.8 60237 42361 910.90 ... 399.5 236 2140.0 108.1
2 4860.3 59447 43725 961.00 ... 523.7 249 2350.0 110.7
3 5301.8 62067 45296 1230.40 ... 675.4 266 2570.0 112.8
4 5937.4 65040 46436 1430.10 ... 892.5 289 2849.4 114.5
5 7206.7 70904 48197 1832.90 ... 1214.7 327 3376.4 117.7
6 8986.1 76501 49873 2543.20 ... 1622.6 437 4305.0 128.1
7 10201.4 80850 51282 3120.50 ... 2238.5 452 4950.0 135.8
8 11954.5 86632 52783 3791.70 ... 3081.4 550 5820.0 145.7
9 11922.3 92997 54334 4763.80 ... 3822.2 692 7440.0 172.7
10 16917.8 96934 55329 4410.40 ... 5196.4 762 8101.4 203.4
11 18398.4 95703 63909 4517.00 ... 7119.8 802 8300.1 207.7
12 21662.3 103783 64799 5594.30 ... 9241.6 896 9415.6 213.7
13 26651.9 109170 65554 8080.10 ... 11759.4 1070 10993.7 225.2
14 34360.5 113993 66373 13072.30 ... 15203.5 1331 12462.1 254.9
15 46670.0 122737 67199 17042.10 ... 21318.8 1746 16264.7 310.2
16 57494.9 131176 67947 20019.30 ... 29662.3 2236 20620.0 356.1
17 66830.3 138946 68850 22913.50 ... 38520.8 2641 24774.1 377.8
18 73142.7 138173 69500 24914.10 ... 46279.8 2834 27298.9 380.5
19 76967.1 132214 69957 28406.20 ... 53407.5 2972 29153.5 370.9
20 80422.8 122000 70586 29834.70 ... 59621.8 3143 31134.7 359.8
>>> y
array([[ 1146.38],
[ 1139.53],
[ 1173.79],
[ 1212.33],
[ 1366.95],
[ 1642.86],
[ 2004.82],
[ 2122.04],
[ 2199.35],
[ 2357.24],
[ 2664.9 ],
[ 2937.1 ],
[ 3149.48],
[ 3483.37],
[ 4348.93],
[ 5158.1 ],
[ 6242.2 ],
[ 7407.99],
[ 9651.14],
[ 9875.95],
[11444.05]])模型检验
>>> lrModel.score(x,y)
0.9971458875882132确定公式
查看截距
>>> alpha = lrModel.intercept_[0]
>>> alpha
2425.6858933074127查看参数
>>> beta = lrModel.coef_[0]
>>> beta
array([ 0.1000633 , -0.06393532, 0.06399272, -0.09941855,
6.08718343, -0.1251754 , -5.19932315, 1.07558855,
-16.21937074])
最后公式为
>>> y =2425.6858933074127 + 0.1000633x1 - 0.06393532x2 + 0.06399272x3 - 0.09941855x4 + 6.08718343x5 - 0.1251754x6 - 5.19932315x7 + 1.07558855x8 - 16.21937074x9从结果可知,对财政数据影响正相关的有 x1国内生产总值,x3从业人员总数,x5实际利用外资总额,x8消费品零售总额,x9居民消费总数。
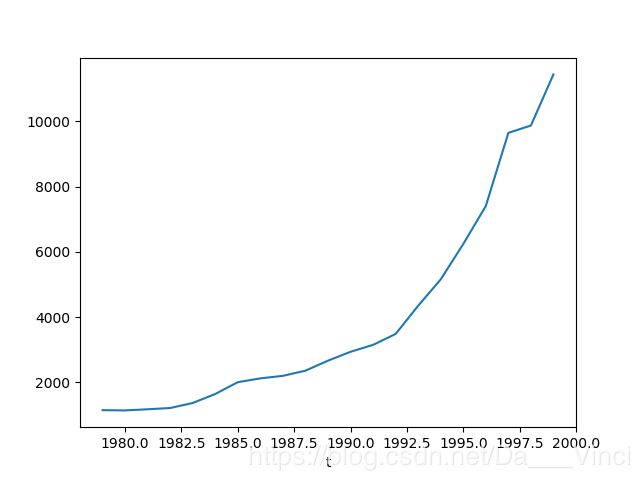
>>> data['y'].plot()
分析结果
(1)从我们上面的步骤来看,我国财政增长具有相当的惯性
(2)财政收入对GDP的依存度较低,这反映出改革开放以来,我国财政收入占GDP的比重出现逐年下滑的客观事实。
(3)财政收入对能源消费总量x2和全社会固定资产投资总额出现轻微负相关,说明我国的消费结构发生了一些变化
(4)x3从业人数总额和x8零售品消费总额对财政收入正相关,这一直都是相辅相成的