#使用SAS进行变量筛选、模型诊断、多元线性回归分析 #
转载, 太经典了,学习了
来源: http://blog.sina.com.cn/s/blog_70a384770102v56h.html
第一节 多元线性回归分析的概述
回归分析中所涉及的变量常分为自变量与因变量。当因变量是非时间的连续性变量(自变量可包括连续性的和离散性的)时,欲研究变量之间的依存关系,多元线性回归分析是一个有力的研究工具。
多元回归分析的任务就是用数理统计方法估计出各回归参数的值及其标准误差;对各回归参数和整个回归方程作假设检验;对各回归变量(即自变量)的作用大小作出评价;并利用已求得的回归方程对因变量进行预测、对自变量进行控制等等。
值得注意的是∶一般认为标准化回归系数的绝对值越大,所对应的自变量对因变量的影响也就越大。但是,当自变量彼此相关时,回归系数受模型中其他自变量的影响,若遇到这种情况,解释标准化回归系数时必须采取谨慎的态度。当然,更为妥善的办法是通过回归诊断(The Diagnosis of Regression),了解哪些自变量之间有严重的多重共线性(Multicoll-inearity),从而,舍去其中作用较小的变量,使保留下来的所有自变量之间尽可能互相独立。此时,利用标准化回归系数作出解释,就更为合适了。
关于自变量为定性变量的数量化方法
设某定性变量有k个水平(如ABO血型系统有4个水平),若分别用1、2、…、k代表k个水平的取值,是不够合理的。因为这隐含着承认各等级之间的间隔是相等的,其实质是假定该因素的各水平对因变量的影响作用几乎是相同的。
比较妥当的做法是引入k-1个哑变量(Dummy Variables),每个哑变量取值为0或1。现以ABO血型系统为例,说明产生哑变量的具体方法。
当某人为A型血时,令X1=1、X2=X3=0;当某人为B型血时,令X2=1、X1=X3=0;当某人为AB型血时,令X3=1、X1=X2=0;当某人为O型血时,令X1=X2=X3=0。
这样,当其他自变量取特定值时,X1的回归系数b1度量了E(Y/A型血)-E(Y/O型血)的效应; X2的回归系数b2度量了E(Y/B型血)-E(Y/O型血)的效应; X3的回归系数b3度量了E(Y/AB型血)-E(Y/O型血)的效应。相对于O型血来说,b1、b2、b3之间的差别就较客观地反映了A、B、AB型血之间的差别。
[说明] E(Y/)代表在“”所规定的条件下求出因变量Y的期望值(即理论均值)。
5.变量筛选
研究者根据专业知识和经验所选定的全部自变量并非对因变量都是有显著性影响的,故筛选变量是回归分析中不可回避的问题。然而,筛选变量的方法很多,详见本章第3节,这里先介绍最常用的一种变量筛选法──逐步筛选法。
模型中的变量从无到有,根据F统计量按SLENTRY的值(选变量进入方程的显著性水平)决定该变量是否入选;当模型选入变量后,再根据F统计量按SLSTAY的值(将方程中的变量剔除出去的显著性水平)剔除各不显著的变量,依次类推。这样直到没有变量可入选,也没有变量可剔除或入选变量就是刚剔除的变量,则停止逐步筛选过程。在SAS软件中运用此法的关键语句的写法是∶
MODEL Y = 一系列的自变量 / SELECTION=STEPWISE SLE=p1 SLS=p2;
具体应用时,p1、p2应分别取0~1之间的某个数值。
6.回归诊断
自变量之间如果有较强的相关关系,就很难求得较为理想的回归方程;若个别观测点与多数观测点偏离很远或因过失误差(如抄写或输入错误所致),它们也会对回归方程的质量产生极坏的影响。对这两面的问题进行监测和分析的方法,称为回归诊断。前者属于共线性诊断(The Diagnosis of Collinearity)问题;后者属于异常点诊断(The Diagnosis ofOutlier)问题。下面结合SAS输出结果作些对应的解释,详细讨论参见第4节。
第二节 应用举例
[例1] 某精神病学医生想知道精神病患者经过6个月治疗后疾病恢复的情况Y是否能通过精神错乱的程度X1、猜疑的程度X2两项指标来较为准确地预测。资料如下,试作分析。
Y X1 X2
28 3.36 6.9
24 3.23 6.5
14 2.58 6.2
21 2.81 6.0
22 2.80 6.4
10 2.74 8.4
28 2.90 5.6
8 2.63 6.9
23 3.15 6.5
16 2.60 6.3
13 2.70 6.9
22 3.08 6.3
20 3.04 6.8
21 3.56 8.8
13 2.74 7.1
18 2.78 7.2
先建立数据文件pdh.txt,输成16行3列的形式。这是二元线性回归分析问题。由于自变量个数很少,先尝试用不筛选自变量的方法建立回归方程,视结果的具体情况再确定后续方案。
(程序1)
dm ‘log;clear;output;clear;’;
DATA abc1;
INFILE ‘d:\zerocv\pdh.txt’;
INPUT y x1 x2;
PROC REG;
MODEL y=x1 x2;
RUN;
程序1很简单,它拟合Y关于X1、X2的二元线性回归方程;从运算结果得知∶ 方程的截距项与0之间无显著性差别(红色框),表明可将截距项去掉(加上选择项NOINT),于是,产生了如下:
(程序2)
DATA abc2;
INFILE 'd:\zerocv\pdh.txt';
INPUT y x1 x2;
PROC REG;
MODEL y=x1 x2 / NOINT P R;
RUN;
使用SAS进行变量筛选、模型诊断、多元线性回归分析
这是程序2的方差分析和参数估计结果,方程与各参数的检验结果都有显著性意义,所求得的二元线性回归方程为∶Y^=17.806056X1-4.873584X2,SY.X=2.53714。SY.X是回归模型误差的均方根,此值越小,表明所求得的回归方程的精度越高(下同)。
使用SAS进行变量筛选、模型诊断、多元线性回归分析
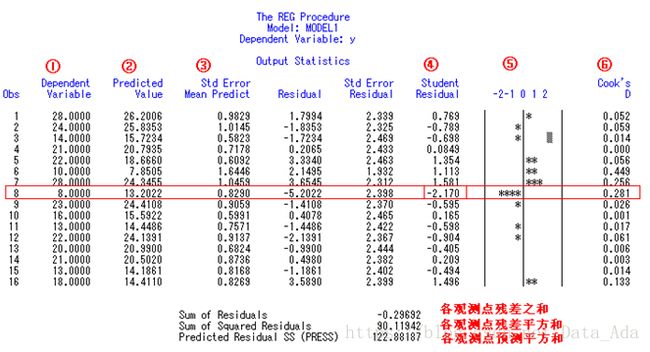
这是对程序2中的二元回归模型作残差分析的结果,从第④、⑤两列发现第8个观测点所对应的学生化残差的绝对值大于2(因STUDENT=-2.170),故认为该点可能是异常点,需认真检查核对原始数据。
第①~③列分别为因变量的观测值、预测值及其标准误差;其后的普通残差及其标准误差被省略了;第⑥列为Cook’s D统计量及预测平方和Press的定义参见本章第6节。
程序2的运算结果表明∶第8个观测点为可疑的异常点,试着将此点剔除后看看结果有什样的变化,产生了程序3。
(程序3)
DATA abc3;
INFILE ‘d:\zerocv\pdh.txt’;
INPUT y x1 x2;
IF N=8 THEN DELETE;
PROC REG;
MODEL y=x1 x2 / NOINT P R;
RUN;
使用SAS进行变量筛选、模型诊断、多元线性回归分析
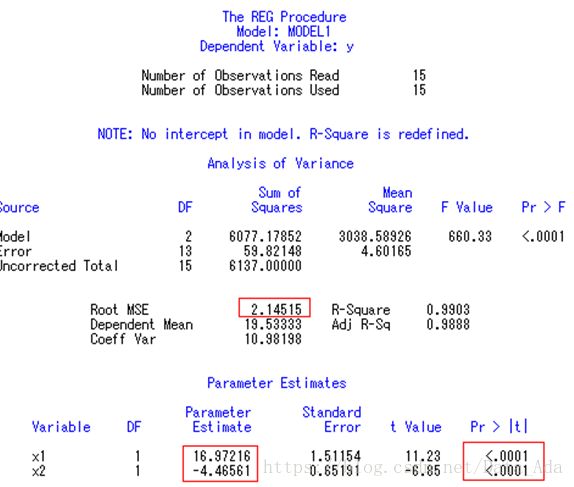
这是程序3的方差分析和参数估计结果,方程与各参数的检验结果都有显著性意义(p值均小于0.0001),所求得的二元线性回归方程为∶Y^=16.972158X1-4.465611X2, SY.X=2.14515。
使用SAS进行变量筛选、模型诊断、多元线性回归分析
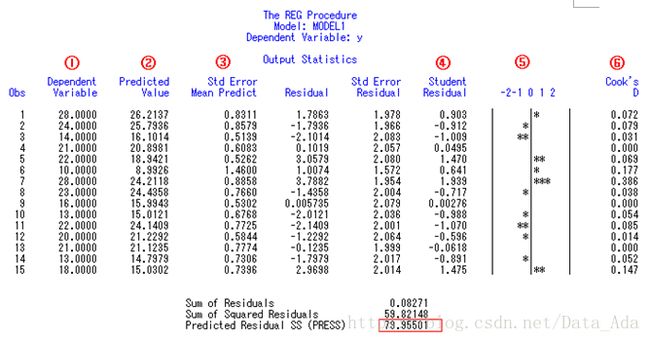
这是对程序3中的二元回归模型作残差分析的结果,没有发现异常点(第四列没有绝对值大于2的记录)。比较第8个观测点去掉前后预测平和Press的值从122.8819降为79.9550;对整个方程检验的F值从474.661上升为660.326,表明该点对因变量预测值的影响是比较大的,值得注意
程序2与程序3MODEL语句中的选择项P、R分别要求计算各点上因变量的预测值和进行残差分析。欲求标准化回归系数,可在MODEL语句的“/”之后加上“STB”。
[结论] 可用二元线性回归方程Y^=16.972158X1-4.465611X2较好地预测因变量Y的的值,回归方程误差均方根为 =2.14515。
[例2] 有人在某地抽样调查了29例儿童的血红蛋白与4种微量元素的含量,资料如下,试问∶可否用4种微量元素(单位都是μmol/L)钙(X1)、镁(X2)、铁(X3)、铜(X4)来较好地预测血红蛋白(Y,g/L)的含量?为回答所提的问题,选用多元线性回归分析较合适。先将数据按29行5列的形式输入,建立数据文件BLOOD.txt
Y X1 X2 X3 X4
135.0 13.70 12.68 80.32 0.16
130.0 18.09 17.51 83.65 0.26
137.5 13.43 21.73 76.18 0.19
140.0 16.15 16.10 84.09 0.19
142.5 14.67 15.48 81.72 0.16
127.5 10.90 10.76 70.84 0.09
125.0 13.70 12.68 80.32 0.16
122.5 21.49 18.00 78.78 0.28
120.0 15.06 15.70 70.60 0.18
117.5 13.48 14.07 72.60 0.20
115.0 15.28 15.35 79.83 0.22
112.5 15.01 13.84 68.59 0.14
110.0 17.39 16.44 74.59 0.21
107.5 18.03 16.49 77.11 0.19
105.0 13.75 13.57 79.80 0.14
102.5 17.48 15.13 73.35 0.19
100.0 15.73 14.41 68.75 0.13
97.5 12.16 12.55 61.38 0.15
95.0 13.04 11.15 58.41 0.13
92.5 13.03 14.87 69.55 0.16
90.0 12.40 10.45 59.27 0.14
87.5 15.22 12.03 46.35 0.19
85.0 13.39 11.83 52.41 0.21
82.5 12.53 11.99 52.38 0.16
80.0 16.30 12.33 55.99 0.16
78.0 14.07 12.04 50.66 0.21
75.0 16.50 13.12 61.61 0.11
72.5 18.44 13.54 55.94 0.18
70.0 11.80 11.73 52.75 0.13
[程序修改指导] 由于自变量不太多,为便于对全部变量都参入计算的结果有一个全面的了解,先用程序1作试探性分析,并用了共线性诊断的技术。
值得注意的是∶用来实现共线性诊断的选择项有①COLLIN、②COLLINOINT两个,①对截距未进行校正,②对截距进行了校正。若MODEL语句中加了选择项/NOINT(即方程中不包含截距项),此时,①、②的输出结果完全相同,故只需写其中一个即可;若MODEL语句中未加选择项/NOINT(即方程中包含截距项),此时,①、②的输出结果之间差别大小视截距项的检验结果有无显著性而有所不同。当截距项无显著性意义时,①、②的输出结果差别很小,用其中任何一个结果都是可以的,参见本例程序1的输出结果;当截距项有显著性意义时,①、②的输出结果差别较大,应该用由②输出的结果,参见在本例结尾所给的[样例]。
若希望对异常点进行诊断,可在MODEL语句的“/”号之后加上选择项INFLUNENCE。 由于程序1运行的结果表明“截距项无显著性意义”,提示应将截距项从模型中去掉,于是,产生了程序2。MODEL语句中各选择项的含义是∶NOINT不要截距项、STEPWISE用逐步回归法筛选自变量、SLE=0.3规定选变量进入方程的显著性水平为0.3、 SLS=0.1规定从方程中剔除变量的显著性水平为0.1、STB要求求出标准化回归参数的估计值。
(程序1)
DATA abc1;
INFILE ‘d:\zerocv\blood.txt’;
INPUT y x1-x4;
PROC reg;
MODEL y=x1-x4 / COLLIN COLLINOINT;
RUN;
使用SAS进行变量筛选、模型诊断、多元线性回归分析
程序1的参数估计结果∶截距项Intercept、X2、X4都无显著性意义(p值较大),但不应过早将X2、X4从模型中去掉。最好等截距项从模型中去掉之后,重新拟合,视最后的结果再作决定。
使用SAS进行变量筛选、模型诊断、多元线性回归分析
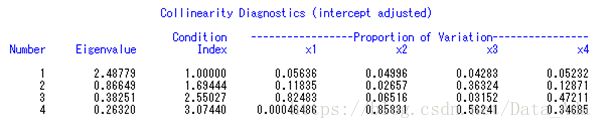
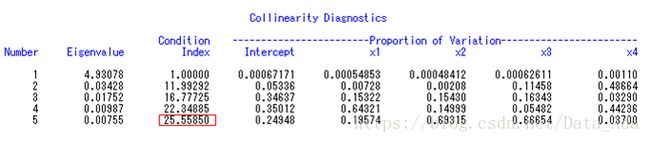
这是共线性诊断的第1部分,即未对截距项校正的回归诊断结果∶从最后一行的条件数25.5585>10(概念参见本章第4节)可知,自变量之间有较强的共线性;从该行方差分量 (对大的条件数(Condition index),通常大于10认为条件数大,会有共线性变量,而contition index>30认为条件数非常大,严重的共线性变量,考察大的条件数所在行,同时有2个以上变量的方差分量超过50%,就意味这些变量间有一定程度的相关,也即该图中Proportion of Variation中有某行同时有2各或以上的值超过50%,则可认为有共线性)的数值可看出∶自变量之间的共线性主要表现在X2、X3两变量上。
使用SAS进行变量筛选、模型诊断、多元线性回归分析
这是共线性诊断的第2部分,即对截距项校正之后的回归诊断结果∶因本例的截距项无显著性意义,故用第1部分诊断结果就可以了。
(程序2)
DATA abc2;
INFILE ‘d:\zerocv\blood.txt’;
INPUT y x1-x4;
PROC reg;
MODEL y=x1-x4 / NOINT
SELECTION=STEPWISE SLE=0.30 SLS=0.10 STB;
RUN;
使用SAS进行变量筛选、模型诊断、多元线性回归分析
使用SAS进行变量筛选、模型诊断、多元线性回归分析
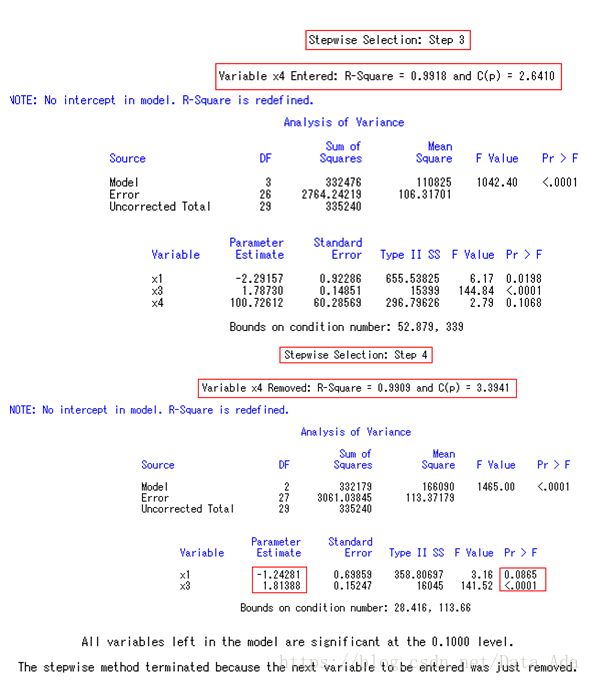
这是程序2中逐步回归分析的结果。 筛选的最后结果表明∶ 只有X1和X3进入筛选;X3是有非常显著性影响的变量;而X1仅在P=0.0865水平上有显著性意义,若规定SLS=0.05,则回归方程中只有X3一个自变量。
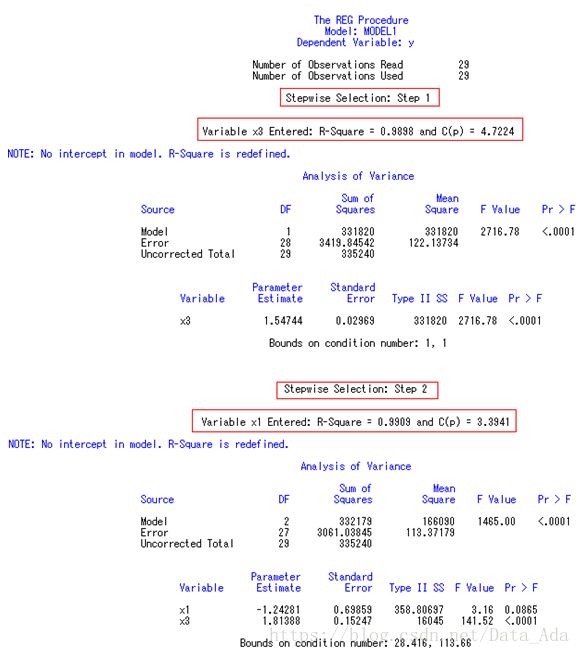
逐步回归分析的最后结果,回归方程为∶Y^=-1.242806X1+1.813880X3
两个标准化回归系数分别为-0.174394、1.166184,结合前面共线性诊断的结果可知, X1与X3之间无密切的相关关系,故可认为X3对Y的影响大于X1。
[专业结论] 微量元素中铁(X3)的含量对血红蛋白(Y)的影响有非常显著性意义。铁的吸收量提高后,有助于血红蛋白含量的提高(因B3=1.16618>0);而钙的吸收量提高后,反而会使血红蛋白含量有减少的趋势(因B1=-0.17439<0)。
[例3] 某项试验研究中,有5个自变量X1~X5和1个因变量Y(资料见下面的SAS程序)。试拟合Y关于5个自变量的回归方程,并用COLLIN和COLLINOINT两个选择项进行回归诊断。
DATA DEF;
INPUT X1-X5 Y @@; CARDS;
64 14 20 224 100 24.08 70 14 18 236 100 25.67
64 16 24 242 100 28.59 72 16 22 212 100 25.31
66 18 28 218 85 27.88 72 18 26 230 85 31.53
66 20 18 242 85 27.99 74 20 30 206 85 28.03
68 22 22 218 85 27.77 74 22 20 230 85 31.31
68 24 26 236 70 31.21 76 24 24 206 70 29.16
70 26 30 212 70 30.83 76 26 28 224 70 36.39
;
PROC REG;
MODEL Y=X1-X5 / COLLIN COLLINOINT;
RUN;
使用SAS进行变量筛选、模型诊断、多元线性回归分析
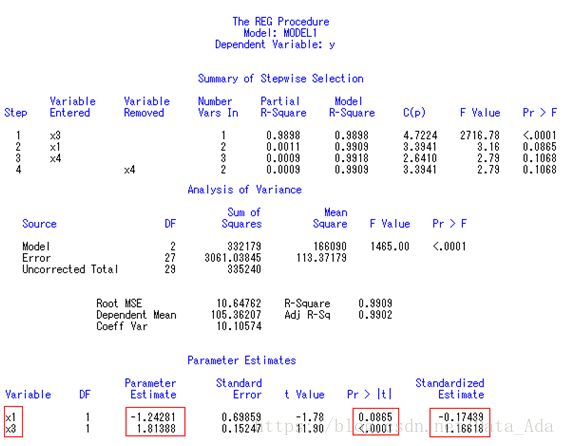
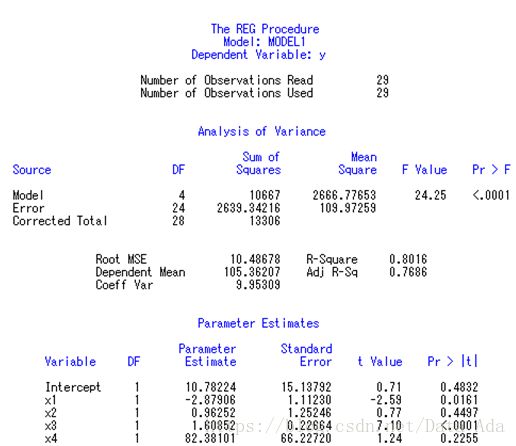
总回归模型有非常显著性意义(Pr>F的p值较小,且r-square接近1),截距项有显著性意义(Intercept项的p值较小)。
使用SAS进行变量筛选、模型诊断、多元线性回归分析
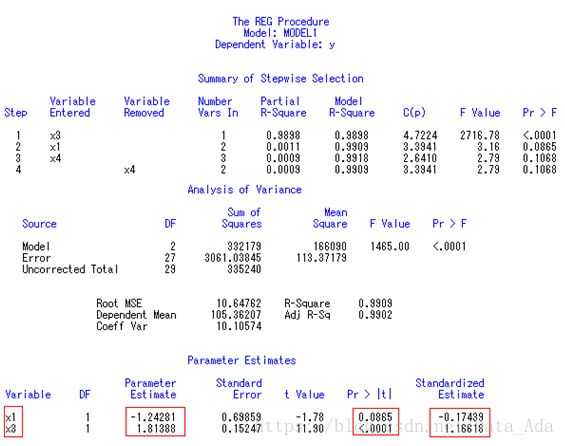
这是选择项COLLIN输出的结果,由于截距项有显著性意义,故在未对截距项进行校正的共线性诊断结果中几乎看不出哪些自变量之间有共线性关系。所以需要先对截距项进行校正后进行共线性诊断,看下面的输出。
使用SAS进行变量筛选、模型诊断、多元线性回归分析
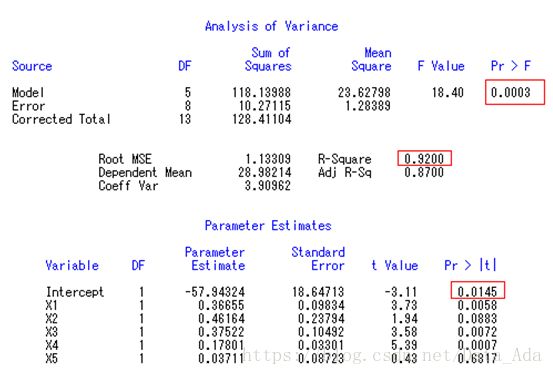
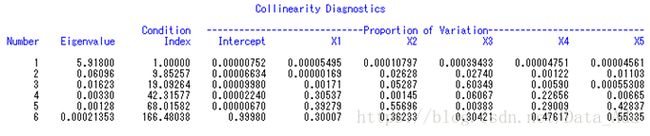
这是选择项COLLINOINT输出的结果,由于截距项有显著性意义,故从对截距项进行校正后的共线性诊断结果,从该行方差分量(对大的条件数(Condition index),通常大于10认为条件数大,会有共线性变量,而contition index>30认为条件数非常大,严重的共线性变量,考察大的条件数所在行,同时有2个以上变量的方差分量超过50%,就意味这些变量间有一定程度的相关,也即该图中Proportion of Variation中有某行同时有2各或以上的值超过50%,则可认为有共线性)的数值可看出∶第5列中X2与X5的值均超过90%,且条件数为7.6,故认为X2与X5之间存在一定的共线性关系。
第三节变量筛选方法
当所研究的问题涉及较多的自变量时,我们很难想象事先选定的全部自变量对因变量的影响都有显著性意义,也不敢保证全部自变量之间是相互独立的。换句话说,在建立多元线性回归方程时,需要根据各自变量对因变量的贡献大小进行变量筛选,剔除那些贡献小、与其他自变量有密切关系的自变量,发现那些对回归方程有很坏影响的观测点(这些都是回归诊断的重要内容,参见第4节),从而求出精练的、稳定的回归方程。
在运用SAS中REG或STEPWISE等过程进行回归分析时,是通过MODEL语句对模型作出初步假设,然后就要根据实验数据和统计规则,选择模型中的变量和估计回归参数。对于线性模型而言,在REG中可以同时采用以下8种选择变量的方法,现逐一加以介绍。
1.向前选择法(FORWARD)
模型中变量从无到有依次选一变量进入模型,并根据该变量在模型中的Ⅱ型离差平和(SS2)计算F统计量及P值。当P小于SLENTRY(程序中规定的选变量进入方程的显著性水平)则该变量入选,否则不能入选;当模型中变量少时某变量不符合入选标准,但随着模型中变量逐次增多时,该变量就可能符合入选标准;这样直到没有变量可入选为止。SLENTRY缺省值定为0.5,亦可定为0.2到0.4,如果自变量很多,此值还应取得更小一些,如让SLENTRY=0.05。
向前选择法的局限性∶SLENTRY取值小时,可能任一个变量都不能入选;SLENTRY大时,开始选入的变量后来在新条件下不再进行检验,因而不能剔除后来变得无显著性的变量。
2.向后消去法(BACKWARD)
从模型语句中所包含的全部变量开始,计算留在模型中的各个变量所产生的F统计量和P值,当P小于SLSTAY(程序中规定的从方程中剔除变量的显著性水平)则将此变量保留在方程中,否则,从最大的P值所对应的自变量开始逐一剔除,直到模型中没有变量可以剔除时为止。SLSTAY缺省值为0.10,欲使保留在方程中的变量都在α=0.05水平上显著时,应让SLSTAY=0.05。
程序能运行时, 因要求所选自变量的子集矩阵满秩,所以当观测点少、且变量过多时程序会自动从中选择出观测点数减1个变量。
向后消去法的局限性∶SLSTAY大时,任一个变量都不能剔除;SLSTAY小时,开始剔除的变量后来在新条件下即使有了显著性,也不能再次被入选回归模型并参入检验。
3.逐步筛选法(STEPWISE)
此法是向前选择法和向后消去法的结合。模型中的变量从无到有像向前选择法那样,根据F统计量按SLENTRY水平决定该变量是否入选;当模型选入变量后,又像向后消去法那样,根据F统计量按SLSTAY水平剔除各不显著的变量,依次类推。这样直到没有变量可入选,也没有变量可剔除或入选变量就是刚剔除的变量,则停止逐步筛选过程。
逐步筛选法比向前选择法和向后消去法都能更好地在模型中选出变量,但也有它的局限性∶其一,当有m个变量入选后,选第m+1个变量时,对它来说,前m个变量不一定是最佳组合;其二,选入或剔除变量仅以F值作标准,完全没考虑其他标准。
4.最大R2增量法(MAXR)
首先找到具有最大决定系数R2的单变量回归模型,其次引入产生最大R2增量的另一变量。然后对于该两变量的回归模型,用其他变量逐次替换,并计算其R2,如果换后的模型能产生最大R2增量,即为两变量最优回归模型,如此再找下去,直到入选变量数太多,使设计矩阵不再满秩时为止。
它也是一种逐步筛选法,只是筛选变量所用的准则不同,不是用F值,而是用决定系数R2判定变量是否入选。因它不受SLENTRY和SLSTAY的限制,总能从变量中找到相对最大者;胀克服了用本节筛选法1~3法时的一种局限性∶找不到任何变量可进入模型的情况。
本法与本节第3种方法都是逐步筛选变量方法,每一步选进或剔除变量都是只限于一个,因而二者局限性也相似∶第一,当有m个变量入选后,选第m+1个变量时,对它来说,前m个变量不一定是最佳组合;第二,选入或剔除变量仅以R2值作标准,完全没考虑其他标准。
5.最小R2增量法(MINR)
首先找到具有最小决定系数R2的单变量回归模型,然后从其余变量中选出一个变量,使它构成的模腥其他变量所产生的R2增量最小,不断用新变量进行替换老变量,依次类推,这样就会顺次列出全部单变量回归模型,最后一个为单变量最佳模型;两变量最小R2增量的筛选类似本节第4种方法,但引入的是产生最小R2增量的另一变量。对该两变量的回归模型,再用其他变量替换,换成产生最小R2增量者,直至R2不能再增加,即为两变量最优回归模型。依次类推,继续找含3个或更多变量的最优回归模型等等,变量有进有出。
它与本节第4种方法选的结果不一定相同,但它在寻找最优模型过程中所考虑的中间模型要比本节第4种方法多。
本法的局限性与本节第3、4种方法相似∶第一,当有m个变量入选后,选第m+1个变量时,每次只有1个变量进或出,各变量间有复杂关系时,就有可能找不到最佳组合;第二,选入变量或替换变量仅以R2值作标准,完全没考虑其他标准。
6.R2选择法(RSQUARE)
从模型语句中的各自变量所有可能子集中选出规定数目的子集,使该子集所构成的模型的决定系数R2最大。要注意∶当观测点少、且模型语句中变量数目过多时, 程序不能运行,因为过多变量使误差项无自由度,设计矩阵不满秩,所以最多只能从所有可能的变量中选择观测点数减1个变量放入模型。本法和后面的本节第7、8种方法分别是按不同标准选出回归模型自变量的最优子集,这类选变量法不是从所有可能形成的变量中,而仅仅从模袖量中穷举。
本法的局限性在于∶其一,当样本含量小于等于自变量(含交互作用项)个数时,只能在一定数目的变量中穷举,为找到含各种变量数目的最优子集,要么增加观测,要么反复给出不同模型;其二,选最优子集的标准是R2,完全没考虑其他标准。
7.修正R2选择法(ADJRSQ)
根据修正的决定系数R2取最大的原则,从模型的所有变量子集中选出规定数目的子集。程序能运行的条件是设计矩阵X满秩。
本法的局限性与本节第6种方相似: 其一,与本节第6种方中“其一”相同;其二,选最优子集的标准只是用修正的R2取代未修正的R2而已,完全没考虑其他标准。
8.Mallow’s Cp选择法(CP)
根据Mallow’s Cp统计量(定义见本章第6节),从模袖量子集中选出最优子集。 Cp统计量的数值比本节第6、7种方法更大地依赖于MODEL语句所给出的模型,它比前二者多考虑的方面是∶用模型语句决定的全回归模型估计出误差平和。程序能运行的条件是设计矩阵满秩。
本法的局限性与本节第6种方相似,只是用Cp统计量取代R2而已。
[说明1] 全回归模型选择(NONE)∶不舍弃任何变量,将全部变量都放入模型之中去。当各回归模型中的各回归变量的设计矩阵不满秩时,与本节第6~8种方法选择方法同样道理,回归分析是不能正常进行下去的。
[说明2] 用本节第6~8种方法只能达到筛选变量的目的,但结果中并没有具体给出回归方程各参数的估计值及其检验结果,需从所给出的变量组合中结合专业知识选择某些变量子集,用不筛选变量的方法建立含所指定变量子集的回归方程。
[说明3] 用本节第1~5种方法虽然给出了筛选变量后的回归方程,但一般也只用于变量筛选,当确定了最后的回归方程之后,此时,再在模型语句的“/”号之后多加一些选择项,重新运行修改后的程序,以便给出各种检验、诊断和描述性的结果。
第四节 回归诊断方法
回归诊断的两项主要任务
(1)检验所选模型中的各变量之间共线性(即某些自变量之间有线性关系)情况;
(2) 根据模型推算出与自变量取各样本值时对应的因变量的估计值y^,反过来检验所测得的Y是否可靠。
下面就SAS系统的REG过程运行后不同输出结果,仅从回归诊断方面理解和分析说明1.用条件数和方差分量来进行共线性诊断
各入选变量的共线性诊断借助SAS的MODEL语句的选择项COLLIN或COLLINOINT来完成。二者都给出信息矩阵的特征根和条件数(Condition Number),还给出各变量的方差在各主成分上的分解(Decomposition),以百分数的形式给出,每个入选变量上的方差分量之和为1。COLLIN和COLLINOINT的区别在于后者对模型中截距项作了校正。当截距项无显著性时,看由COLLIN输出的结果;反之,应看由COLLINOINT输出的结果。
(1)条件数
先求出信息矩阵X’X的各特征根, 条件指数(condition indices)定义为: 最大特征根与每个特征根比值的平根,其中最大条件指数k称为矩阵X’X的条件数。
条件数大,说明设计矩阵有较强的共线性,使结果不稳定,甚至使离开试验点的各估计值或预测值毫无意义。
直观上,条件数(condition index)度量了信息矩阵X’X的特征根散布程度,可用来判断多重共线性是否存在以及多重共线性严重程度。在应用经验中,若0<k<10,则认为没有多重共线性;10≤k≤30,则认为存在中等程度或较强的多重共线性;k>30,则认为存在严重的多重共线性。
(2)方差分量
强的多重共线性同时还会表现在变量的方差分量上∶同一行中同时有2个以上变量的方差分量超过50%,就意味这些变量间有一定程度的相关。
2.用方差膨胀因子来进行共线性诊断
(1)容许度(Tolerance,在Model语句中的选择项为TOL)
对一个入选变量而言,该统计量等于1- R2,这里R2是把该自变量当作因变量对模型中所有其余回归变量的决定系数, R2大(趋于1),则1-R2=TOL小(趋于0),容许度差,该变量不由其他变量说明的部分相对很小。
(2)方差膨胀因子(VIF)
VIF=1/TOL,该统计量有人译为“方差膨胀因子”(Variance Inflation Factor),对于不好的试验设计,VIF的取值可能趋于无限大。VIF达到什么数值就可认为自变量间存在共线性?尚无正规的临界值。[陈希孺、王松桂,1987]根据经验得出∶VIF>5或10时,就有严重的多重共线性存在。
3.用学生化残差对观测点中的强影响点进行诊断
对因变量的预测值影响特别大,甚至容易导致相反结论的观测点,被称为强影响点(In-fluence Case)或称为异常点(Outlier)。有若干个统计量(如∶Cook’ D统计量、hi统计量、STUDENT统计量、RSTUDENT统计量等,这些统计量的定义参见第6节)可用于诊断哪些点对因变量的预测值影响大,其中最便于判断的是学生化残差STUDENT统计量,当该统计量的值大于2时,所对应的观测点可能是异常点,此时,需认真核对原始数据。若属抄写或输入数据时人为造成的错误,应当予以纠正;若属非过失误差所致,可将异常点剔除后再作回归分析。如果有可能,最好在此点上补做试验,以便进一步确认可疑的“异常点”是否确属异常点。
第五节 用各种筛选变量方法编程的技巧
从第3节可知,有多种筛选变量的方法,这些方法中究竟哪一种最好?没有肯定的答复。最为可行的做法是对同一批资料多用几种筛选变量的方法,并结合专业知识从中选出相对优化的回归模型。
判断一个回归模型是否较优,可从以下两个方面考虑∶其一,整个回归模型及模型中各回归参数在统计学上有显著性意义、在专业上(特别是因变量的预测值及回归方程的精度)有实际意义;其二,在包含相同或相近信息的前提下,回归方程中所包含的变量越少越好。
下面利用一个小样本资料,通过一个较复杂的SAS程序,展示如何用各种筛选变量的方法实现回归分析、如何用已求得的回归方程对资料作进一步的分析的技巧。
[例4] α-甲酰门冬酰苯丙氨酸甲酯(FAPM)是合成APM的关键中间体之一。试验表明,影响FAPM收率的主要因素有∶ 原料配比(r)、溶剂用量(p1)、催化剂用量(p2)及反应时间(t)等4个因素,现将各因素及其具体水平的取值列在下面。
影响FAPM合成收率的因素和水平∶
因素各水平的代码 1 2 3 4 5 6 7
r 原料配比 0.80 0.87 0.94 1.01 1.08 1.15 1.22
p1 溶剂用量(ml) 10 15 20 25 30 35 40
p2 催化剂用量(g) 1.0 1.5 2.0 2.5 3.0 3.5 4.0
t 反应时间(h) 1 2 3 4 5 6 7
研究者按某种试验设计方法选定的因素各水平的组合及其试验结果如下,试用回归分析方法分析此资料(注∶权重仅为相同试验条件下重复实验运行的次数)。
编号 r p1 p2 t Y(收率,%) 权重
1 0.80 15 2.0 6 71.5 3
2 0.87 25 3.5 5 71.2 2
3 0.94 35 1.5 4 72.8 3
4 1.01 10 3.0 3 69.7 2
5 1.08 20 1.0 2 67.5 3
6 1.15 30 2.5 1 67.3 3
7 1.22 40 4.0 7 71.8 3
[SAS程序]
dm ‘log;clear;output;clear;’;
OPTIONS PS=70;
DATA ex3;
INPUT r p1 p2 t y w;
rp1=r*p1; rt=r*t; p1t=p1*t; r2=r*r; t2=t*t; p12=p1*p1; p22=p2*p2;
- 这里产生的7个新变量代表因素之间的交互作用;
CARDS;
0.80 15 2.0 6 71.5 3
0.87 25 3.5 5 71.2 2
0.94 35 1.5 4 72.8 3
1.01 10 3.0 3 69.7 2
1.08 20 1.0 2 67.5 3
1.15 30 2.5 1 67.3 3
1.22 40 4.0 7 71.8 3
;
RUN;
PROC REG ;
MODEL y=r r2 p1 p12 p2 p22 t t2 rp1 rt p1t / SELECTION=FORWARD;
MODEL y=r r2 p1 p12 p2 p22 t t2 rp1 rt p1t / SELECTION=BACKWARD;
MODEL y=r r2 p1 p12 p2 p22 t t2 rp1 rt p1t / SELECTION=STEPWISE;
MODEL y=r r2 p1 p12 p2 p22 t t2 rp1 rt p1t / SELECTION=MAXR START=1 STOP=5;
MODEL y=r r2 p1 p12 p2 p22 t t2 rp1 rt p1t /SELECTION=MINR START=1 STOP=5;
MODEL y=t t2 p12 r rp1 / SELECTION=RSQUARE BEST=30 STOP=5;
MODEL y=t t2 p12 r rp1 / SELECTION=ADJRSQ BEST=30 STOP=5;
MODEL y=t t2 p12 r rp1 / SELECTION=CP BEST=40 STOP=5;
RUN;
- 用选好的模型分析数据,并给出关于模型的各种统计量(计权重);
PROC REG;
WEIGHT w;
MODEL y=r rp1 p12 t2 / SELECTION=NONE P CLI INFLUENCE STB COLLIN COLLINOINT;
RUN;
DATA b; * 先将原始数据放入数据集b ;
SET ex3 END=EOF;
OUTPUT;
- 再按照r , p1 , t的合理范围形成y为缺失的数据也放入数据集b;
IF EOF THEN DO;
y=.;
DO r=0.8 TO 1.22 BY .7;
do p1=10 to 40 BY 5;
DO t=1 TO 7;
rp1=r*p1; rt=r*t; p1t=p1*t; r2=r*r; t2=t*t; p12=p1*p1;OUTPUT;
END;
END;
END;
END;
RUN;
- 按原始数据回归,却可得到r、p1、t的新组合所对应的估计值y^;
PROC REG DATA=b ;
WEIGHT w;
MODEL y=r rp1 p12 t2 / P CLI CLM COLLINOINT STB R VIF;
OUTPUT OUT=d1 PREDICTED=pdc;
RUN;
PROC PRINT DATA=d1; RUN;
PROC SORT DATA=d1(KEEP=r p1 t pdc); BY DESCENDING pdc; RUN;
DATA c;
SET d1;
FILE PRINT;
TITLE '40 best combinations of r p1 t ';
IF _N_<=40 THEN PUT ' r='r:4.2 ' p1='p1:2.0 ' t=' t:1.0 ' y=' pdc:8.5;
* 对于各因素各水平取值区间的不同组合,求出估计值,列出其中40个收率较高的组合;
RUN;
[SAS程序修改指导] 至于模型1~模型8等号右边每次究竟应该写哪些自变量(含它们的交互作用项),基本上是在结合专业知识的基础上凭经验进行摸索,一般需多次调试。若观测点数n远远大于自变量的个数k时,可将全部自变量放入MODEL语句中,用不同的方法进行筛选;若n≤k,有些方法最多只能用n-1个变量参入筛选。
[说明] 此程序的输出结果太多,从略。
第6节 与回归分析有关的重要统计术语和统计量的注解
1.R-square(决定系数、复(全)相关系数平)
(1)复相关系数为因变量的观测值y与估计值(y^)之间的简单线性相关系数
(2)决定系数
其中,各入选变量总的回归贡献(即回归离差平和)SSR可分别表示成下列①、②两种形式∶
① (即各回归系数与Siy相乘再求和,其中 。
② (即总离均差平和与总误差平和之差)。
2.校正的R2 (Adjusted R-square )
R2随模型中的变量的增加而增加,且不会减小,模型中的变量太多可能因共线性而不稳定,所以看一个模型好坏,不仅要看R2,而且还应看R2adj,后者对自由度(也即变量数)作了校正。
3.Mallows’ Cp统计量
当从k个回归变量中选出p个时,为鉴别模型好坏,可用Mallows’ Cp统计量(一般认为, Cp近似等于p较好),它与总观测数(n)、MODEL语句所考虑的总变量数(k)、运算中当前选入模型的变量数(p)、总的误差平和(SSEk)、该模型的误差平和(SSEp)有关:
此式中的第1项还可用下面两种表达形式∶①MSEp·(n-p-1)/MSEk ;②SSEp/MSEk
Cp的定义公式中第1项的3种形式是等式变换,注意到下面两个均方的定义,则不难看懂它们之间的关系。MSEp=SSEp/(n-p-1)、 MSEk=SSEk/(n-k-1)。
4.剩余或残差(Residual)
①普通残差, RESIDi=ei=yi-y^i ;
②学生化残差Studentized residual, STUDENTi=ei/STDERR(ei) ;
③学生化剔除残差Studentized deleted residual, (有人称为刀切法残差Jackknife residual),
RSTUDENT=ei/(S(i)*p),在MODEL语句中加上INFLUENCE后就会给出各点上RSTUDENT统计量的值,如果单用选择项R,只给出普通残差和STUDENT的计算结果。
④预测平和,Press=∑ni=1[ei/(1-hi)]2,它度量了全模型的优劣。
5.COOK’S D(库克距离)统计量
对某一观测引起的影响(INFLUENCE)的度量,通过计算此观测在模型中和不在模型中引起COOK’S D统计量的变化来衡量。[约瀚·内特等,1990]认为∶COOK’S D>50%时,就可以认为第i个观测点对回归函数的拟合有强的影响。