【机器学习】决策树剪枝优化及可视化

前言

\quad\quad 前面，我们介绍了分类决策树的实现，以及用 sklearn 库中的 DecisionTreeClassifier 和 DecisionTreeRegressor 类实现了分类决策树和回归决策树的一些案例。

• 具体可见：分类决策树与回归决策树

其中，我们也对决策树的不同深度对模型的欠拟合和过拟合的影响进行了比较。

本篇源代码可见：Github

一、欠拟合与过拟合

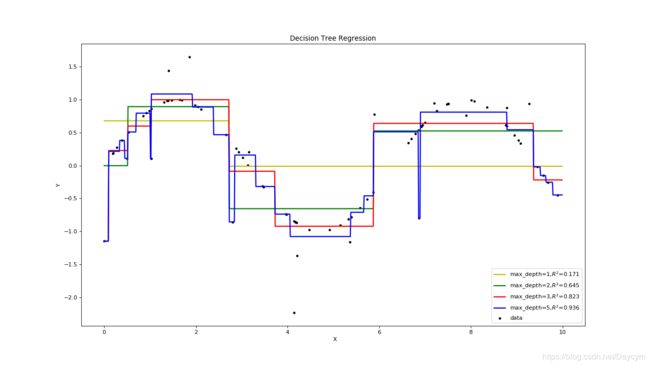
\quad\quad 我们在构建决策树的时候，为了尽可能正确分类训练样本，节点划分过程不断重复，有时候就会导致决策树节点过多，使得模型对训练样本学得 “过好” ，以至于把训练样本的一些个别特征信息也当做一般性质，从而导致 “过拟合”；如果节点过少，就会导致训练样本的特征信息不能够很好的学习到，从而导致 “欠拟合”。

图中，蓝色的线由于学习训练样本的太好，将噪声信息也学习到了，所以导致了过拟合；而黄色的线，决策树深度只有一层，说明只划分了一次，明显出现了欠拟合。

对此，我们可以通过主动去掉一些分支来降低过拟合的风险，也就是 “剪枝处理”。

二、剪枝处理

决策树的剪枝处理是决策树算法中最基本、最有用的一种优化方案，主要分为两大类：

• 前置剪枝：

前置剪枝是指在决策树生成过程中，对每个节点在划分前先进行评估，若当前节点的划分不能够给模型带来泛化性能的提升，则停止划分并将当前节点标记为叶节点；

• 后置剪枝：

后置剪枝则是先从训练样本生成一棵完整的决策树，然后 自底向上 地对非叶节点进行考察，若将该节点对应的子树替换为叶节点能够给模型带来泛化性能的提升，则将该子树替换为叶节点。

那么我们如何查看模型的泛化性能是否提升呢？

下面我们通过周志华的《机器学习》中的西瓜数据来详细介绍剪枝过程。假设有如下西瓜数据：

• 训练集

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
–	–	–	–	–	–	–	–
10	青绿	硬挺	清脆	清晰	平坦	软粘	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

• 测试集

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	是
–	–	–	–	–	–	–	–
9	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
11	浅白	硬挺	清脆	模糊	平坦	硬滑	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	否
13	青绿	稍蜷	浊响	稍糊	稍凹	硬滑	否

1、由测试集构建决策树

• 计算原信息熵：
  $$p(好{瓜}_{是})=\frac{1}{2}p(好{瓜}_{否})=\frac{1}{2}$$
  $$Ent(D)=-\frac{1}{2}log\frac{1}{2}-\frac{1}{2}log\frac{1}{2}=1$$

• 计算第一个特征色泽的信息熵

$$p(青绿)=\frac{4}{10}=\frac{2}{5}p(乌黑)=\frac{4}{10}=\frac{2}{5}p(浅白)=\frac{2}{10}=\frac{1}{5}$$
$$p(好瓜|青绿)=\frac{2}{4}=\frac{1}{2}p(坏瓜|青绿)=\frac{2}{4}=\frac{1}{2}$$
$$p(好瓜|乌黑)=\frac{3}{4}p(坏瓜|乌黑)=\frac{1}{4}$$
$$p(好瓜|浅白)=0p(坏瓜|浅白)=1$$
$$Ent(青绿)=-\frac{1}{2}log\frac{1}{2}-\frac{1}{2}log\frac{1}{2}=1$$
$$Ent(乌黑)=-\frac{3}{4}log\frac{3}{4}-\frac{1}{4}log\frac{1}{4}\approx 0.8113$$
$$Ent(浅白)=-0log0-1log1=0$$
$$Gain(色泽)=Ent(D)-p(青绿)Ent(青绿)-p(乌黑)Ent(乌黑)-p(浅白)Ent(浅白)\approx 0.276$$

• 同理求得其他特征的信息增益
  $$Gain(根蒂)=0.115Gain(敲声)=0.174Gain(纹理)=0.174$$
  $$Gain(脐部)=0.276Gain(触感)=0$$

我们根据最大信息增益来划分属性选择，上面有两个一样，我们选择脐部作为根节点来划分：

然后，我们针对每个子树重复执行以上计算，便可以得到完整的决策树：

2、前置剪枝

对于第一个划分属性：脐部

• 划分前：验证集精度为 $\frac{3}{7}\ast 100$
• 划分后：验证集精度为 $\frac{5}{7}\ast 100$

验证集精度提高了，所以继续划分

前置剪枝，如果选择根节点为脐部的时候，我们用验证集去验证划分前和划分后的验证集精度，如果划分后，验证集精度提高了，说明划分可以带来决策树模型的泛化性能，那么就划分；如果划分后，验证集精度没提高或降低，说明划分后不可以带来性能的提升，那么就停止划分。

• 由图可知，前置剪枝使得决策树的很多分支都没有“展开”，这不仅降低了过拟合的风险，还显著减少了决策树的训练开销和测试时间；
• 但是有些分支的当前划分虽然不能提升泛化性能、甚至可能导致泛化性能暂时下降，但在其基础上进行的后续划分却可能导致性能明显提高；
• 因此，前置剪枝禁止分支展开，给决策树带来了欠拟合的风险。

3、后置剪枝

后置剪枝先从训练样本生成一棵完整的决策树，然后基于验证集数据，按照完整决策树计算出验证集的精度为：
$$\frac{3}{7}=42.9$$

后置剪枝，先判断原纹理节点处，剪枝前后的验证集精度

• 剪枝前验证集精度为42.9%；剪枝后验证集精度为57.1%，所以决定剪枝。
• 即将纹理节点所在子树分支减去，将纹理节点变为叶节点，然后用多数表决法，根据原纹理节点下的数据决定剪枝后该叶节点的标记为好瓜。
• 然后再以同样的方式处理其他节点，从下至上处理，直到根节点

三、决策树可视化

决策树可视化可以方便我们直观的观察所构建的树模型；决策树可视化依赖graphviz服务，所以我们在进行可视化之前，安装对应的服务：

• 安装graphviz服务

1. 下载安装包(msi安装包)：官网
2. 执行下载好的安装包(双击msi安装包)；
3. 将graphviz的根目录下的bin文件夹路径添加到PATH环境变量中；

• 安装python的graphviz插件： pip install graphviz
• 安装python的pydotplus插件： pip install pydotplus

决策树可视化方式：

• 方式一：将模型输出dot文件，然后使用graphviz的命令将dot文件转换为pdf格式的文件
• 方式二：直接使用pydotplus插件直接生成pdf文件进行保存
• 方式三：使用Image对象直接显示pydotplus生成的图片

1、回归决策树可视化

本案例以波士顿房屋租赁数据训练回归决策树，然后将生成的回归决策树直接生成图片。

实现步骤：

• 读取数据
• 数据处理
• 数据分割
• 数据归一化
• 模型构建、训练
• 模型可视化

from sklearn import tree
import pydotplus
dot_data = tree.export_graphviz(dtr, out_file=None,  
                         filled=True, rounded=True,  
                         special_characters=True)  
graph = pydotplus.graph_from_dot_data(dot_data)  
graph.write_png('tree.png')

常用参数说明：

可查看官方文档帮助

• decision_tree：要导出到GraphViz的决策树；
• out_file：输出文件的名称；
• filled： bool, optional (default=False)：设置为时True，绘制节点以指示用于分类的多数类，用于回归的极值，或用于多输出的节点的纯度。
• rounded : bool, optional (default=False) ：设置为时True，绘制带圆角的节点框并使用Helvetica字体而不是Times-Roman。
• special_characters：bool，optional（default= False）：设置False为时，忽略PostScript兼容性的特殊字符。

另外还有两个：

• feature_names：特征名称；
• class_names：目标类的名称，按升序排列；

代码可见： 10_回归决策树模型可视化.py

2、分类决策树可视化

本案例以鸢尾花数据训练分类决策树，基本步骤和上面一样，并通过三种方式分别实现可视化。

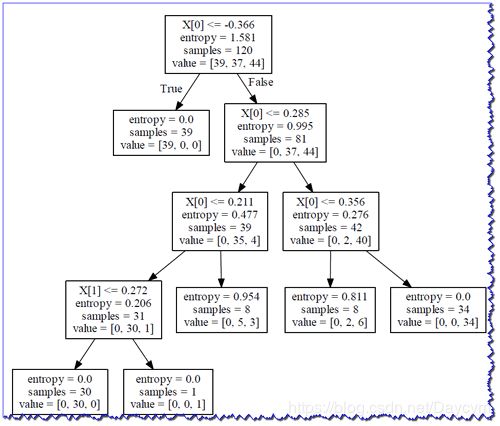
## a.方式一：输出形成dot文件，然后使用graphviz的dot命令将dot文件转换为pdf
from sklearn import tree
with open('iris.dot', 'w') as f:
    # 将模型model输出到给定的文件中
    f = tree.export_graphviz(model, out_file=f)
# 命令行执行dot命令： dot -Tpdf iris.dot -o iris.pdf

• iris.dot文件
  

• 命令行执行dot命令： dot -Tpdf iris.dot -o iris.pdf，生成iris.pdf文件
  

## b.方式二：直接使用pydotplus插件生成pdf文件 pip install pydotplus
from sklearn import tree
import pydotplus 
dot_data = tree.export_graphviz(model, out_file=None) 
graph = pydotplus.graph_from_dot_data(dot_data) 
graph.write_pdf("iris1.pdf") 

结果和上面的 iris.pdf 一样

from sklearn import tree
import pydotplus
dot_data = tree.export_graphviz(model, out_file=None,
						feature_names=['sepal length', 'sepal width', 'petal length', 'petal width'],  
                        class_names=['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'], 
                        filled=True, rounded=True,  
                        special_characters=True)  
graph = pydotplus.graph_from_dot_data(dot_data)  
graph.write_png("iris.png")

四、决策树模型中的 min_samples_split 参数

通过设置min_samples_split 参数：拆分内部节点所需的最小样本数；

# 上图设置的为10
DecisionTreeClassifier(criterion='entropy', random_state=0, min_samples_split=10)
# 下图设置的为5
DecisionTreeClassifier(criterion='entropy', random_state=0, min_samples_split=5)

由两幅图可知，数值越小决策树分支越多

• 当设置为10的时候，也就是叶节点中样本数小于10的时候就可以停止划分
• 当设置为5的时候，表示叶节点样本数小于5的时候才可以停止划分

# 下图设置为2
DecisionTreeClassifier(criterion='entropy', random_state=0, min_samples_split=2)

可以看出，样本数大于等于2的节点右进行了划分

由此，可见min_samples_split 参数相当于进行了剪枝处理