一维搜索算法介绍及其实现
一维搜索算法介绍及其实现
当进行优化算法实现时、一般都要进行一系列如下格式的迭代运算
x(k+1) = x(k) + a(k) *s(k)，其中s(k)是变量变化的方向，而a(k)可以确定变量变化的大小，即我们平时所说的步长，a(k)被称为学习率。求最佳步长即求一元函数:
的极值问题，这一过程被称为一维搜索。一维搜索也是解多维最优化问题的重要支柱。
一维搜索一般有如下方法，解析法和数值解法。解析法即是按照数学公式求导数求极值。但是一般实际问题中，往往不知道损失函数的数学表达式、或者导数比较难求，这种方法一般应用于科学计算。数值类方法有分为两类，试探法和插值法。
二、确定初始单谷区间的进退法
为了进行一维搜索，我们首先需要缩小变量所在的变化范围，然后再用其他方法去求极值。
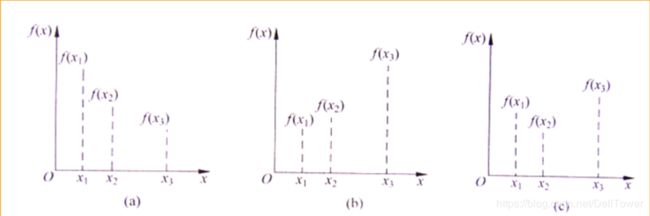
如图所示，对于单谷函数而言，有如下结论
若
，则极小点位于点x2的右边区间。
若
，则极小点位于点x2的左边区间。
若
，则极小点位于点x1和点x2之间的区间。
x1和x3就是包含一个极小点的区间。
这几个结论告诉我们，只有我们能够找到三点x1,x2,x3使得三点满足条件
x1
进退法的步骤
1、选定初始点x1,初始步长h，x2 = x1 + h，计算y1 = f(x1),y2 = f(x2)
2、比较y1 和y2
（a）y1 > y2，那么我们已经找到了符合条件的x1和x2，可以继续下一步.
（b）y1 < y2，那么我们找错了方向，应该反向搜搜，将x1 与x2互换，并将h= -h
（c）y1 = y2 ，终止程序，极小值点在区间[x1,x2]之间。
3、产生新的探测点x3 = x2 +h ,y3 = f(x3)
4、比较y2和y3
（a）y2 > y3 ，那么赋值x1 = x2, x2 = x3，转步骤3 继续进行探测。
（b）y2< y3，那么我们已经找到三个符合条件的点了。
极小值所在的区间为[min(x1,x3), max(x1,x3)]
三、区间消退法
搜索区间确定后，在搜索区间[a,b]内任取两点a1 b1
若f(a1) < f(b1)，则取[a, b1]为缩短后的搜索区间,反之则取[a1, b]为搜索后的区间，如此迭代下去，当精度满足时，则停止迭代。
四、黄金分割法
黄金分割法也是逐步缩小区间，不过它是按照一定比例进行缩小，步骤如下。
在搜索区间[a,b]，若精度不满足要求，则下次的搜索区间为
a1 = a + 0.382(b-a)
b1 = a + 0.618(b-a)
当精度满足时，则停止迭代。
代码参考地址https://github.com/delltower/machine_learn