Octave快速入门（转载）

原文链接https://blog.csdn.net/iszhenyu/article/details/78712228

以下是我的补充：

PS1('>>') 将原来的octave:1>提示输入改成>>提示输入。

octave:75> PS1('>>')
>>

randn(m,n)  函数生成一个m行n列的矩阵，矩阵的所有元素服从高斯分布，均值为0，标准差或者方差为1。

hist(变量）为对一个随机变量画出直方图。

octave:5> w=-6+sqrt(11)*(randn(1,10000));
octave:6> hist(w)

矩阵/向量

exp(向量) 求以e为底数，以向量中的元素为指数的幂运算

octave:36> exp([1 2 3])
ans =

    2.7183    7.3891   20.0855

其他一些运算：

% a = [1 15 2 0.5]，求最大值
>> val = max(a)
val =  15

% 求最大值，并返回最大值的索引
>> [val, idx] = max(a)
val =  15
idx =  2

% 矩阵对应元素的逻辑运算
>> a <= 1
ans =
   1   0   0   1

% 返回a中小于3的元素的索引
>> find(a < 3)
ans =
   1   3   4

% 计算之和
>> sum(a)  
ans =  18.500

% 计算乘积
>> prod(a)  
ans =  15

% 向下取整（向下取最接近的整数，即直接舍掉小数部分）
>> floor(a)
ans =
    1   15    2    0

% 向上取整（向上取最接近的整数，即小数部分变为加1）
>> ceil(a)
ans =
    1   15    2    1

% 生成一个随机矩阵，矩阵元素的值位于0-1之间
>> rand(3)  
ans =
   0.458095   0.323431   0.648822
   0.481643   0.789336   0.559604
   0.078219   0.710996   0.797278

% 返回一个矩阵，这个矩阵的每个元素取两个随机矩阵对应元素中的最大值的结果
octave:56> max(rand(3),rand(3))
ans =

   0.916676   0.875362   0.881009
   0.409057   0.489740   0.069200
   0.494241   0.633359   0.961897

octave:57> A
A =

   1   2
   3   4
   5   6
% 得到每一列的最大值作为一个行向量，默认。
octave:58> max(A,[],1)      % 同 max(A)
ans =

   5   6

% 得到每一行的最大值作为一个列向量
octave:59> max(A,[],2)
ans =

   2
   4
   6

% 求整个矩阵最大值的两种方法：

% 1.先求每一列的最大值作为一个行向量，再求最大值
octave:61> max(max(A))
ans =  6

% 2.先将A的所有元素变为一个列向量，再求最大值
octave:63> max(A(:))
ans =  6

% 矩阵按行上下对换
>> flipud(eye(4))  
ans =
Permutation Matrix

   0   0   0   1
   0   0   1   0
   0   1   0   0
   1   0   0   0

magic(n）生成一个n维的幻方（每行、列和对角线上的数字和都相等的矩阵）

octave:65> M=magic(8)
M =

   64    2    3   61   60    6    7   57
    9   55   54   12   13   51   50   16
   17   47   46   20   21   43   42   24
   40   26   27   37   36   30   31   33
   32   34   35   29   28   38   39   25
   41   23   22   44   45   19   18   48
   49   15   14   52   53   11   10   56
    8   58   59    5    4   62   63    1

octave:66> sum(M)
ans =

   260   260   260   260   260   260   260   260

octave:67> sum(M,2)
ans =

   260
   260
   260
   260
   260
   260
   260
   260

% 以下是得到对角线和
octave:70> M .* eye(8)
ans =

   64    0    0    0    0    0    0    0
    0   55    0    0    0    0    0    0
    0    0   46    0    0    0    0    0
    0    0    0   37    0    0    0    0
    0    0    0    0   28    0    0    0
    0    0    0    0    0   19    0    0
    0    0    0    0    0    0   10    0
    0    0    0    0    0    0    0    1

octave:71> sum(M .* eye(8))
ans =

   64   55   46   37   28   19   10    1

octave:72> sum(sum(M .* eye(8)))
ans =  260

% 以下是求另一条对角线的和
octave:73> flipud(eye(8))  % 使矩阵垂直翻转
ans =

Permutation Matrix

   0   0   0   0   0   0   0   1
   0   0   0   0   0   0   1   0
   0   0   0   0   0   1   0   0
   0   0   0   0   1   0   0   0
   0   0   0   1   0   0   0   0
   0   0   1   0   0   0   0   0
   0   1   0   0   0   0   0   0
   1   0   0   0   0   0   0   0

octave:74> sum(sum(M .* flipud(eye(8))))
ans =  260

>>t=[0:0.01:0.98];
>>y1 = sin(2 * pi * 4 * t);
>>y2 = cos(2 * pi * 4 * t);
>>plot(t,y1);

 画出的sin函数：

 

 

>>subplot(1,2,1);    %将图像分为一个1*2的格子，现在要使用第一个格子画图

 

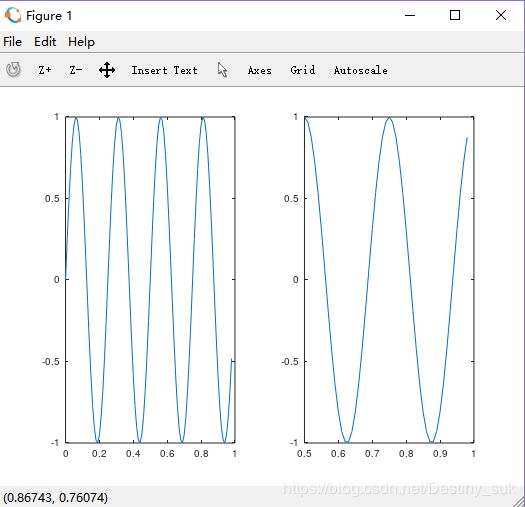
>>plot(t,y1);    % 在当前格子里画那个正弦函数

 

>>subplot(1,2,2);

>>plot(t,y2);

 

>>axis([0.5 1 -1 1]);    % 将横坐标范围改为0.5~1，纵坐标范围改为-1~1。注意因为此时在第二个格子，因此只会改第二个

clf;  清除当前绘图的整个图像

一种数据可视化方向

现在先建一个矩阵

>>A=magic(5);
>>A
A =

   17   24    1    8   15
   23    5    7   14   16
    4    6   13   20   22
   10   12   19   21    3
   11   18   25    2    9

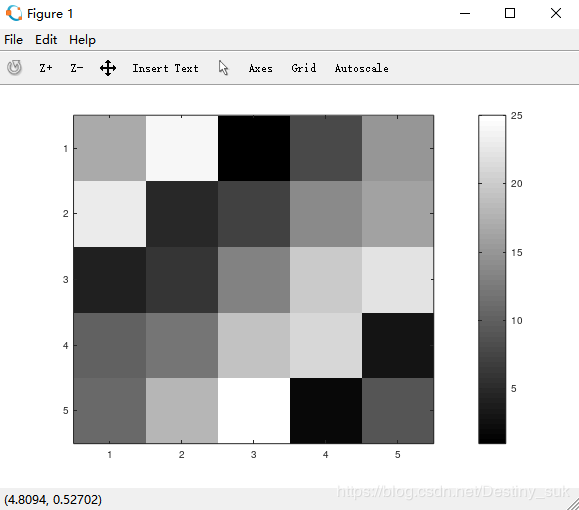
>>imagesc(A)    %将矩阵A中的元素数值按大小转化为不同颜色，并在坐标轴对应位置处以这种颜色染色

>>imagesc(A),colorbar;    % 同时运行这两个函数，colorbar函数显示一个颜色条

将颜色变成灰度的就可以。这样就数值越大的颜色越深，数值越小的颜色越浅。

 

函数

我们还是先看例子，然后再说明具体的写法：

>> function y = squareNum(x)
       y = x^2;
   end;
>> squareNum(3)
ans =  9
1
2
3
4
5

在Octave中，定义一个函数需要使用function 关键字，然后紧跟在 function 后面的是函数的声明，包括返回值，函数名称和参数，之后换行来实现具体的函数功能。

Octave的函数不需要显示的返回语句，Octave会将函数第一行声明的返回值返回给调用方，因此，我们在函数体中只需将最终的计算结果赋给定义的返回值，比如上面例子中的y。

也可以将函数部分写在文件里，文件名命名为“函数名.m”，要注意的就是此.m文件必须在你当前Octave路径下。即以下部分为此文件内容：

function y = squareNum(x)
y = x^2;

 然后在Octave中就可以

还有一点需要说明的是，在Octave中，函数可以返回多个值：

>> function [y1, y2] = calVal(x)
       y1 = x^2;
       y2 = x^3;
   end;
>> [a, b] = calVal(3)
a =  9
b =  27