机器学习实验—线性回归预测

一、实验目的和内容

        1、掌握使用Weka做线性回归的方法；

        2、掌握线性回归的相关知识；

        3、处理丢失数据的值，替换原始数据中的短横线（因为这里的实验数据本应该是数字类型，而不是枚举类型）。

二、实验过程

         1、下载安装Weka

        下载不包含Java运行环境的安装包，下载之后按照提示安装软件，实验前电脑上已经安装Java运行环境。

        配置Java环境。安装配置完成。
        2、数据预处理：
        这里我们要介绍一下WEKA中的术语。表格里的一个横行称作一个实例（Instance），相当于统计学中的一个样本，或者数据库中的一条记录。竖行称作一个属性（Attribute），相当于统计学中的一个变量，或者数据库中的一个字段。这样一个表格，或者叫数据集，在WEKA看来，呈现了属性之间的一种关系(Relation)。
        WEKA存储数据的格式是ARFF（Attribute-Relation File Format）文件，这是一种ASCII文本文件。
        需要注意的是，在Windows记事本打开这个文件时，可能会因为回车符定义不一致而导致分行不正常。我使用UltraEdit查看ARFF文件的内容。
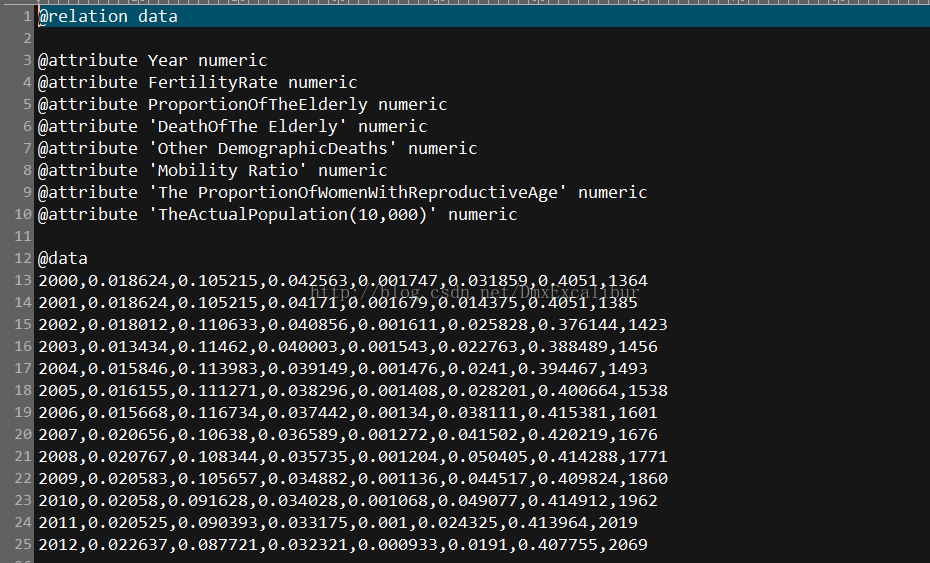
        下面我们来对这个文件的内容进行说明。 
        识别ARFF文件的重要依据是分行，因此不能在这种文件里随意的断行。空行（或全是空格的行）将被忽略。 
        以“%”开始的行是注释，WEKA将忽略这些行。如果你看到的“xx.arff”文件多了或少了些“%”开始的行，是没有影响的。 
        除去注释后，整个ARFF文件可以分为两个部分。第一部分给出了头信息（Head information），包括了对关系的声明和对属性的声明。第二部分给出了数据信息（Data information），即数据集中给出的数据。从“@data”标记开始，后面的就是数据信息了。
        关系声明 
        关系名称在ARFF文件的第一个有效行来定义，格式为 

@relation  

        是一个字符串。如果这个字符串包含空格，它必须加上引号（指英文标点的单引号或双引号）。
        属性声明 
        属性声明用一列以“@attribute”开头的语句表示。数据集中的每一个属性都有它对应的“@attribute”语句，来定义它的属性名称和数据类型。 
        这些声明语句的顺序很重要。首先它表明了该项属性在数据部分的位置。例如，“humidity”是第三个被声明的属性，这说明数据部分那些被逗号分开的列中，第三列数据 85 90 86 96 ... 是相应的“humidity”值。其次，最后一个声明的属性被称作class属性，在分类或回归任务中，它是默认的目标变量。
        属性声明的格式为 

@attribute  

        其中是必须以字母开头的字符串。和关系名称一样，如果这个字符串包含空格，它必须加上引号。 
        WEKA支持的有四种，分别是 ：

numeric-------------------------数值型 

-----分类（nominal）型 

string----------------------------字符串型 

date []--------日期和时间型 

        其中 和 将在下面说明。还可以使用两个类型“integer”和“real”，但是WEKA把它们都当作“numeric”看待。注意“integer”，“real”，“numeric”，“date”，“string”这些关键字是区分大小写的，而“relation”“attribute ”和“date”则不区分。
        数值属性 
        数值型属性可以是整数或者实数，但WEKA把它们都当作实数看待。
        分类属性 
        分类属性由列出一系列可能的类别名称并放在花括号中：{, , , ...} 。数据集中该属性的值只能是其中一种类别。
        例如如下的属性声明说明“outlook”属性有三种类别：“sunny”，“ overcast”和“rainy”。而数据集中每个实例对应的“outlook”值必是这三者之一。

@attribute outlook {sunny, overcast, rainy} 

        如果类别名称带有空格，仍需要将之放入引号中。
        字符串属性 
        字符串属性中可以包含任意的文本。这种类型的属性在文本挖掘中非常有用。

        示例： 

@ATTRIBUTE LCC string

        日期和时间属性 
        日期和时间属性统一用“date”类型表示，它的格式是 

@attribute date [] 

        其中是这个属性的名称，是一个字符串，来规定该怎样解析和显示日期或时间的格式，默认的字符串是ISO-8601所给的日期时间组合格式“yyyy-MM-ddTHH:mm:ss”。
        数据信息部分表达日期的字符串必须符合声明中规定的格式要求（下文有例子）。
        数据信息 
        数据信息中“@data”标记独占一行，剩下的是各个实例的数据。
        每个实例占一行。实例的各属性值用逗号“,”隔开。如果某个属性的值是缺失值（missing value），用问号“?”表示，且这个问号不能省略。例如：

@data 

sunny,85,85,FALSE,no 

?,78,90,?,yes

        字符串属性和分类属性的值是区分大小写的。若值中含有空格，必须被引号括起来。例如： 

@relation LCCvsLCSH 

@attribute LCC string 

@attribute LCSH string 

@data 

AG5, 'Encyclopedias and dictionaries.;Twentieth century.' 

AS262, 'Science -- Soviet Union -- History.'

        日期属性的值必须与属性声明中给定的相一致。例如： 

@RELATION Timestamps 

@ATTRIBUTE timestamp DATE "yyyy-MM-dd HH:mm:ss" 

@DATA 

 "2001-04-03 12:12:12" 

"2001-05-03 12:59:55"

        稀疏数据 
        有的时候数据集中含有大量的0值（比如购物篮分析），这个时候用稀疏格式的数据存贮更加省空间。 
        稀疏格式是针对数据信息中某个实例的表示而言，不需要修改ARFF文件的其它部分。看如下的数据： 

@data 

0, X, 0, Y, "class A" 

0, 0, W, 0, "class B" 

        用稀疏格式表达的话就是 

@data 

{1 X, 3 Y, 4 "class A"} 

{2 W, 4 "class B"} 

        每个实例用花括号括起来。实例中每一个非0的属性值用 <空格> 表示。是属性的序号，从0开始计；是属性值。属性值之间仍用逗号隔开。这里每个实例的数值必须按属性的顺序来写，如 {1 X, 3 Y, 4 "class A"}，不能写成{3 Y, 1 X, 4 "class A"}。
        注意在稀疏格式中没有注明的属性值不是缺失值，而是0值。若要表示缺失值必须显式的用问号表示出来。
        数据准备
        使用WEKA作数据挖掘，面临的第一个问题往往是我们的数据不是ARFF格式的。幸好，WEKA还提供了对CSV文件的支持，而这种格式是被很多其他软件所支持的。
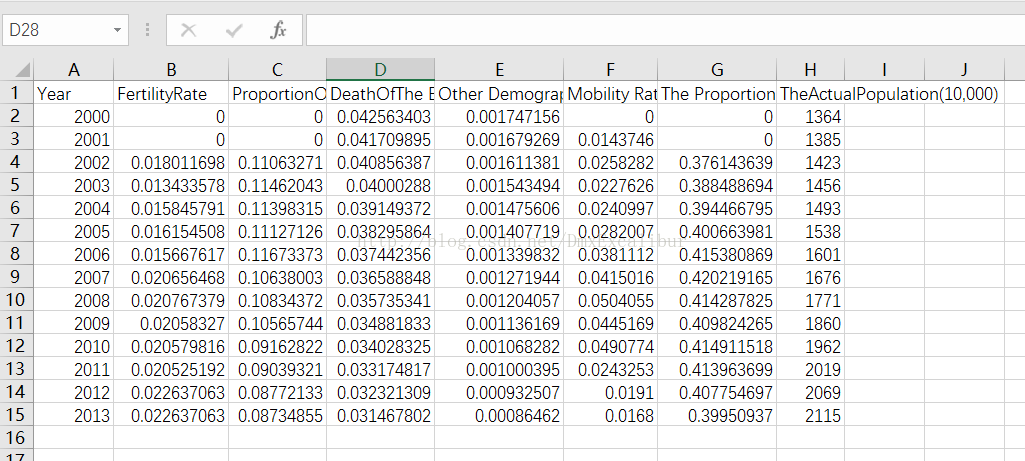
        首先将本实验的数据转存在CSV文件中。

        然后利用Weka包含的Tools将csv转成arff文件，转成之后，将其中确实的数据用“?”代替，截图如下：

        在实验过程中预测当年人口数目是目的，也是这里的因变量，所以，训练数据我把2013这个实例去掉了，根据Weka算出来的模型，以及已有的2013年的各项数据预测出一个人口数目，将这个人口数目和正确答案进行比较即可。

        3、导入arff文件，查看实验结果：

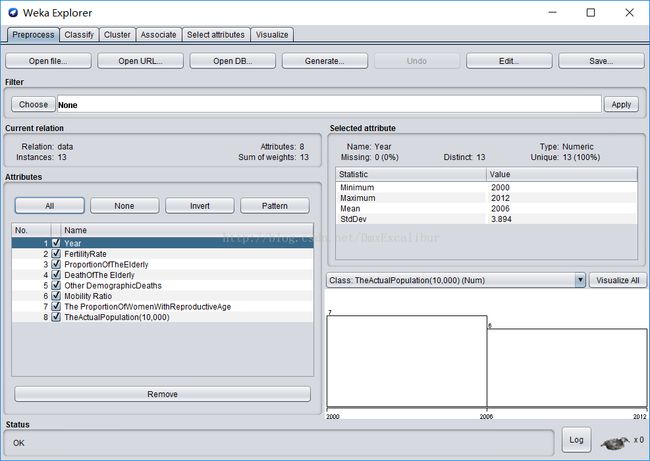
        运行Weka，进入首屏。我们只选择了Explorer 选项。

        进入此界面后点击Open file，加载之前已经处理好的arff文件。
        加载之后的结果如下：

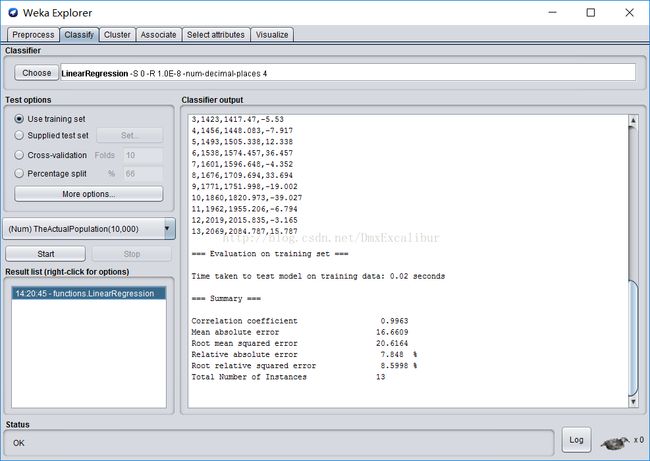
        然后创建回归模型，为了创建这个模型，单击Classify选项卡。单击Choose按钮，然后扩展functions分⽀支。选择LinearRegression叶。
        之后再Test options里面选择Use training set来测试，在More options里面选上output predictions里面的CSV，点击stat会出现结果。

        采用10折交叉验证（10-fold cross validation）来选择和评估模型，在Test options里面选择Cross-validation，点击start，结果如下：

        4、处理丢失数据的值：
        数据的缺失值处理：
        weka.filters.unsupervised.attribute.ReplaceMissingValues。
        对于数值属性，用平均值代替缺失值，对于nominal属性，用它的mode(出现最多的值)来代替缺失值。所以本次试验中对于缺失的数据都采用该属性所有值的平均值来代替：
        处理后的结果为：

        将其转换成Arff文件：

        使用Weka创建回归模型：

        结果和实验三中的一样，包括得到的模型和每一年的预测值，说明Weka在处理丢失数据的时候已经做了均值处理。

三、实验结果

        1、采用10折交叉验证（10-fold cross validation）来选择和评估模型：

        从交叉验证的结果可以看出：
        相关系数为0.9931；
        平均绝对误差为24.6316；
        均方根误差为28.7187；
        相对绝对误差为10.2839%；
        根相对的平方误差为10.6682%；
        实例总数为13。
        2、选择Use training set来训练模型:

inst#,actual,predicted,error

1,1364,1341.491,-22.509

2,1385,1395.021,10.021

3,1423,1417.47,-5.53

4,1456,1448.083,-7.917

5,1493,1505.338,12.338

6,1538,1574.457,36.457

7,1601,1596.648,-4.352

8,1676,1709.694,33.694

9,1771,1751.998,-19.002

10,1860,1820.973,-39.027

11,1962,1955.206,-6.794

12,2019,2015.835,-3.165

13,2069,2084.787,15.787

        这是预测和实际结果的比较，训练出来的模型为：

TheActualPopulation(10,000) =

  -5748.08   * ProportionOfTheElderly +

 -62755.3114 * DeathOfThe Elderly +

   4617.3287

        注：TheActualPopulation(10,000)代表实际人口数（万）。
        该模型：
        相关系数为0.9963；
        平均绝对误差为16.6609；
        根均值平方误差为20.6164；
        相对绝对误差为7.848%；
        根相对平方误差为8。5998%；
        实例总数为13。
        实际2013年的各项数据为：

        将其中的值代入模型预测2013年的实际人口数，那么获得的结果为：

TheActualPopulation(10,000) = -5748.08 * 0.087348549 - 62755.3114 * 0.031467802 + 4617.3287=2140.471。

        2013年的实际人口为2115与预测值的偏差为25.47054.

四、总结

        Weka是一个公开的数据挖掘工作平台，集合了大量能承担数据挖掘任务的机器学习算法，包括对数据进行预处理，分类，回归、聚类、关联规则以及在新的交互式界面上的可视化。它要求的数据格式为Arff，这种数据类似于数据库中的table，但是还是有很大的区别，它定义了数据的每一行为一个实例，每一列为一种属性，最后一个声明的属性被称作class属性，在分类或回归任务中，它是默认的目标变量。本次实验给出的数据并非Arff格式，所以需要转换，那我们就需要现将其转存到CSV文件中去，然后利用Weka包含的Tools来转换成Arff文件，但是由于原数据中有缺失部分，并且缺失部分用“-”代替，这样带来的后果就是，Arff文件中会把这一列的属性定义为分类属性，但实际上其属性为数值属性。这样导致的后果是出现错误的模型，输出的模型我们看不懂是什么含义，那它肯定是一个错误的模型。经过查阅资料之后发现对于缺失的数据用“?”代替，这样系统就会识别到这是缺失数据，如果使用数值0代替效果会不会好呢？答案肯定是不好的。因为缺失数据代表此处没有数据，与此处的值为0训练出来的模型肯定是有差别的，在实际测试中也发现模型的值不一样。

        一般的，若Class属性是分类型时我们的任务才叫分类，Class属性是数值型时我们的任务叫回归。这次实验的目标数据为数值型，所以为线性回归。在统计学中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。本次实验就是利用Weka在生育率、老龄人口占比、老龄人口死亡占比、人口流动比率、女性育龄人口占比这6个自变量和实际人口数之间进行建模分析。

         注：本博客源代码下载地址：http://download.csdn.net/detail/dmxexcalibur/9920658