kuangbin——并查集Java程序

POJ - 2236

思路：裸并查集，但是Java是真的伤；
用TreeSet保存已经接通的节点。
在要接通一个节点时，从已经接通的节点中，找出距离合适的节点，调用Union（）方法。
提交时去掉package语句，将public类名改为Main

package 并查集;

import java.io.BufferedInputStream;
import java.util.Iterator;
import java.util.Scanner;
import java.util.TreeSet;


class Node{
    int x,y;
    public Node(int _x,int _y){
        x=_x;
        y=_y;
    }
}
public class WirelessNetwork {
    static TreeSet set=new TreeSet();
    static int pre[]=new int[1005];
    static Node[] net=new Node[1005];
    static int d;
    static boolean cal(int a,int b)
    {
        if((net[a].x-net[b].x)*(net[a].x-net[b].x)+(net[a].y-net[b].y)*(net[a].y-net[b].y)<=d*d)
            return true;
        return false;
    }
    static void init(int n)
    {
        for(int i=1;i<=n;i++)
            pre[i]=i;
    }
    static int find(int x)
    {
        if(x!=pre[x])
            pre[x]=find(pre[x]);
        return pre[x];
    }
    static void union(int x,int y)
    {
        pre[find(x)]=find(y);
    }
    public static void main(String[]args)
    {
           set.clear();
           int N;
           Scanner cin=new Scanner(new BufferedInputStream(System.in));
           N=cin.nextInt();
           init(N);
           d=cin.nextInt();
           for(int i=1;i<=N;i++)
           {
               int x,y;
               x=cin.nextInt();
               y=cin.nextInt();
               net[i]=new Node(x,y);
           }
           while(cin.hasNext())
           {
               String op=cin.next();
               if(op.equals("O"))
               {

                   int n=cin.nextInt();
                   set.add(n);
                   Iteratorit= set.iterator();
                   while(it.hasNext())
                   {
                       int e=it.next();
                       if(cal(e,n)&&find(n)!=find(e))
                           union(e,n);
                   }
               }
               if(op.equals("S"))
               {
                   int a,b;
                   a=cin.nextInt();
                   b=cin.nextInt();
                   if(find(a)==find(b))
                       System.out.println("SUCCESS");
                   else
                       System.out.println("FAIL");
               }
           }
    }
}

POJ - 1611

思路：合并的时候注意只要有一方的祖先是0，就将其作为共同祖先即可

package 并查集;

import java.io.BufferedInputStream;
import java.util.Scanner;

public class TheSuspects {
    static int pre[]=new int[30005];
    static void init(int n)
    {
        for(int i=0;istatic int find(int x)
    {
        if(x!=pre[x])
            pre[x]=find(pre[x]);
        return pre[x];
    }
    static void union(int x,int y)
    {
        int xx=find(x),yy=find(y);
        if(xx==0)
          pre[yy]=xx;
        else if(yy==0)
            pre[xx]=yy;
        else pre[xx]=yy;
    }
    public  static void main(String []args)
    {
        Scanner cin=new Scanner(new BufferedInputStream(System.in));
        int n,m;
        while(cin.hasNext())
        {
            n=cin.nextInt();
            m=cin.nextInt();
            if(n==0&&m==0) break;
            init(n);
            for(;m>=1;m--)
            {
                int c=cin.nextInt();
                int last=cin.nextInt();
                c--;
                while(c>=1)
                {
                    c--;
                    int e=cin.nextInt();
                    union(last,e);
                    last=e;
                }
            }
            int ans=0;
            for(int i=0;iif(find(i)==0)
                    ans++;
            }
            System.out.println(ans);
        }
    }
}

HDU - 1213

思路：裸并查集

//package 并查集;

import java.io.BufferedInputStream;
import java.util.Scanner;

public class Main {
    static int pre[]=new int[1005];
    static void init(int n)
    {
        for(int i=1;i<=n;i++)
            pre[i]=i;
    }
    static int find(int x)
    {
        if(x!=pre[x])
            pre[x]=find(pre[x]);
        return pre[x];
    }
    static void union(int x,int y)
    {
        pre[find(x)]=find(y);
    }
    public static void main(String[] args)
    {
        int t;
        Scanner cin=new Scanner(new BufferedInputStream(System.in));
        t=cin.nextInt();
        for(int c=1;c<=t;c++)
        {
            int n,m;

            n=cin.nextInt();
            m=cin.nextInt();
            init(n);
            for(int i=1;i<=m;i++)
            {
                int a=cin.nextInt();
                int b=cin.nextInt();
                union(a,b);
            }
            int ans=0;
            for(int i=1;i<=n;i++)
            {
                if(i==find(i))
                    ans++;
            }
            System.out.println(ans);
        }
    }
}

POJ - 1182

思路：种类，或者向量并查集
注意输入输出数据量较大，超过10万！！，需要使用输入挂

Java的输入输出挂见Java输入输出挂

向量并查集就是将关系的更新转化为向量的运算。本题较一般的并查集多了集合内节点之间的关系量，路径更新是要处理好节点与根节点之间的关系。
为啥要叫做向量并查集，关键是节点之间的关系更新可以用向量的运算表示。
下面用图去展示节点关系的更新公式
路径压缩时的关系更新

合并

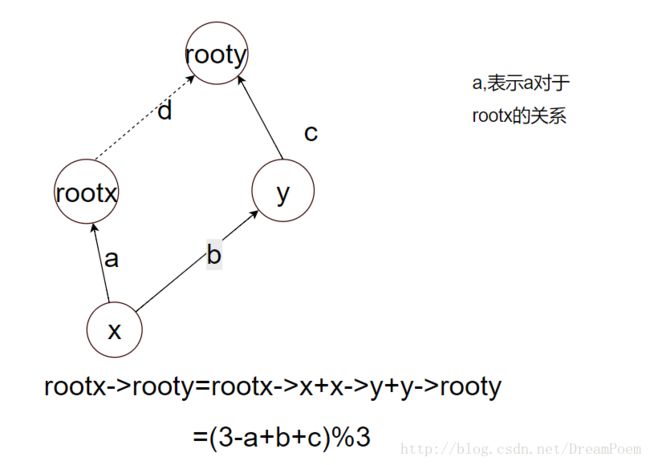
从上上图也可以看出，关系的更新类似于向量的计算。有兴趣的可以下去画图验证一下。
我们用数字0表示x, y是同类;1表示x捕食y；2表示x被y捕食（这样3-op就是x相对y的关系）因此图中出现的%3保证了关系标志的合理范围。

---

输入命令时，判断两者是否在同一个集合，如果不在，则给出的操作是真的，根据命令合并x,y；若两者在同一个集合，根据条件判断x和根节点的关系，y与根节点的关系，列出表达式判断(relation[x]+3-relation[y])%3)!=(op-1) relation[x] 、relation[y]表示x、y关于根节点的关系这个表达式成立说明该所给条件错误。。

import java.io.BufferedInputStream;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Scanner;
import java.util.StringTokenizer;

public class Main {
    static int pre[]=new int[50005];
    static int relation[]=new int[50006];
    static int ans=0,N;
    static void init(int n)
    {
        for(int i=1;i<=n;i++)
        {pre[i]=i;relation[i]=0;}
    }
    static int find(int x)
    {
        if(x!=pre[x])
        {
            int fa=pre[x];
            pre[x]=find(fa);
            relation[x]=(relation[fa]+relation[x])%3;
        }
        return pre[x];
    }
    static void solve(int x,int y,int op)
    {//rel是x对于y的关系
        if(x>N||y>N||(op==2&&x==y))
        {ans++;return;}
        int fa_x,fa_y;
        fa_x=find(x);
        fa_y=find(y);
        if(fa_x==fa_y)
        {
            if(((relation[x]+3-relation[y])%3)!=(op-1))
                ans++;
        }
       else
        {
            pre[fa_x]=fa_y;
            relation[fa_x]=(3-relation[x]+op-1+relation[y])%3;
        }
    }

    public static void main(String []args)
    {
        InputReader cin=new InputReader();
        int K;
        N=cin.nextInt();
        K=cin.nextInt();
        init(N);
        for(int i=1;i<=K;i++)
        {
            int op=cin.nextInt();
            int x=cin.nextInt(),y=cin.nextInt();
            solve(x,y,op);
        }
        System.out.println(ans);
    }
}
class InputReader {
    BufferedReader buf;
    StringTokenizer tok;
    InputReader() {
        buf = new BufferedReader(new InputStreamReader(System.in));
    }
    boolean hasNext() {
        while (tok == null || !tok.hasMoreElements()) {
            try {
                tok = new StringTokenizer(buf.readLine());
            } catch (Exception e) {
                return false;
            }
        }
        return true;
    }
    String next() {
        if (hasNext())
            return tok.nextToken();
        return null;
    }
    int nextInt() {
        return Integer.parseInt(next());
    }

}

HDU - 3038

思路：还是向量并查集；
将关系看作区间和，当现在的条件与已有条件相矛盾，（已知区间和与所给区间和不同）当前条件错误。
本题中用sum[]数组记录子节点与根节点组成的区间的区间和；更新与合并也可用向量运算表示。详情看代码。
对了，题中未交代有多组数据，但是如果不考虑多组数据就一直WA！WA！！WA！！！

import java.io.BufferedInputStream;
import java.util.Scanner;
import java.util.StringTokenizer;

public class Main{
    static int pre[]=new int[200010];
    static int sum[]=new int[200010];
    static int find(int x)
    {
       if(x!=pre[x])
       {
         int fa=pre[x];
         pre[x]=find(fa);
         sum[x]=sum[x]+sum[fa];//更新sum数组
      }
       return pre[x];
    }
    static boolean union(int x,int y,int s)
    {
        int fx=find(x),fy=find(y);
        if(fx==fy)
        {
         if(sum[x]-sum[y]==s) return false;//判断和已知是否相符
          else return true;
        }
        else{
         pre[fx]=fy;
         sum[fx]=s-sum[x]+sum[y];//合并，更新sum数组，可以用向量解释
         return false;
        }
    }
    public static void main(String[]args){
             Scanner cin=new Scanner(new BufferedInputStream(System.in));
             int N,M;
             while(cin.hasNext()) {
              N = cin.nextInt();
              M = cin.nextInt();
              for (int i = 0; i <= N; i++) {
               pre[i] = i;
               sum[i] = 0;
              }
              int ans = 0;
              for (int i = 1; i <= M; i++) {
               int a = cin.nextInt();
               int b = cin.nextInt();
               int s = cin.nextInt();
               a--;//将离散区间，转化为连续区间
               if (union(a, b, s)) ans++;
              }
              System.out.println(ans);
             }
    }
 }