最短路算法总结

一、负权图

在一个图里每条边都有一个权值（有正有负)，如果存在一个环（从某个点出发又回到自己的路径），而且这个环上所有权值之和是负数，那这就是一个负权环，也叫负权回路。存在负权回路的图是不能求两点间最短路的，因为只要在负权回路上不断兜圈子，所得的最短路长度可以任意小。（没有最短路）

单源点的最短路径问题是指：给定一个加权有向图G和源点s，对于图G中的任意一点v，求从s到v的最短路径。

二、最短路

1、Bellman-Ford算法

2、Dijkstra算法(代码以邻接矩阵为例)    &&   Dijkstra + 优先队列的优化(也就是堆优化)

3、floyd-Warshall算法(代码以邻接矩阵为例)

4、SPFA(代码以前向星为例)

5、BFS求解最短路

最短路径的估计值：我们的源点用s表示。在这里我们用数组dis[N]来存储最短路径，dis[N]数组为源点到其他点的最小距离。那么最最开始的最短路径的估计值也就是对dis[N]的初始化。一般我们的初始化都是初始化为 dis[N]= +∞，源点是要初始化为0的，dis[s] = 0,因为s—>s的距离为0;

三、Bellman-Ford

Bellman-Ford算法是求解单源最短路径问题的一种算法。可以判断有无负权回路（若有，则不存在最短路），时效性较好，时间复杂度O（VE）。与Dijkstra算法不同的是，在Bellman-Ford算法中，边的权值可以为负数。设想我们可以从图中找到一个环路（即从v出发，经过若干个点之后又回到v）且这个环路中所有边的权值之和为负。那么通过这个环路，环路中任意两点的最短路径就可以无穷小下去。如果不处理这个负环路，程序就会永远运行下去。而Bellman-Ford算法具有分辨这种负环路的能力。

3.1 Bellman-Ford算法的流程如下：

给定图G(V, E)（其中V、E分别为图G的顶点集与边集），源点s，

·数组Distant[i]记录从源点s到顶点i的路径长度，初始化数组Distant[n]为inf, Distant[s]为0；

·以下操作循环执行至多n-1次，n为顶点数：
对于每一条边e(u, v)，如果Distant[u] + w(u, v) ，则令Distant[v]= Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值；若上述操作没有对Distant进行更新，说明最短路径已经查找完毕，或者部分点不可达，跳出循环。否则执行下次循环；

·为了检测图中是否存在负环路，即权值之和小于0的环路。对于每一条边e(u, v)，如果存在Distant[u] + w(u, v) 的边，则图中存在负环路，即是说该图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。

可知，该算法寻找单源最短路径的时间复杂度为O(V*E)。

3.2 bellman-ford算法求最短路 C/C++版

//起点都从1开始，图采用临接矩阵保存

所用数据结构 ：

struct node
{
    int u, v, w;//u 为起点，v为终点，w为u—>v的权值
};
node edge[100];

bool Bellman_Ford(int s) 

{ 

    for(int i = 1; i <= node_num;i++) //初始化 

        dis[i] =inf; 

    dis[s]=0;

    for(int i = 1; i < node_num; i++) //进行|V|-1次

        for(int j = 1; j <=edge_num; j++) //每个边都判断一次

            if(dis[edge[j].v] >dis[edge[j].u] + edge[j].cost) //对边松弛，边的起点到s的距离，经过该边是否可松弛

            { 

                dis[edge[j].v] =dis[edge[j].u] + edge[j].cost; //dis[edge[j].v] 保存的是edge[j].v到源点的距离

                pre[edge[j].v] =edge[j].u; //保存前驱，即edge[j].v得到这个最短距离的上一步走的是edge[j].u这个节点

            } 

    bool flag = 1; //判断是否含有负权回路 

    for(int i = 1; i <=edge_num; i++) 

         if(dis[edge[i].v]> dis[edge[i].u] + edge[i].cost) 

         { 

             flag = 0; 

             break; 

         } 

    return flag; 

} 

四、Dijkstra(贪心策略)

求单源、无负权的最短路。时效性较好，时间复杂度为O（V*V+E）。当是稀疏图的情况时，此时E=V*V/lgV，所以算法的时间复杂度可为O（V^2）。若是斐波那契堆作优先队列的话，算法时间复杂度，则为O（V*lgV + E）。

因为dijstra是基于贪心策略的，每次出发都是从到源点最小权值的点开始，直到终点。而带负权边的可以从先通过一个不是从到源点最小权值的点开始，经过负权边使总权值变小，例如下面的图

1到2权值3，1到3权值4，3到2权值-2。Dijstra求出的是3，实际的为4-2=2。

4.1 迪杰斯特拉算法简介

迪杰斯特拉（dijkstra）算法是典型的用来解决最短路径的算法，也是很多教程中的范例，由荷兰计算机科学家dijkstra于1959年提出，用来求得从起始点到其他所有点最短路径。该算法采用了贪心的思想，每次都查找与该点距离最近的点，也因为这样，它不能用来解决存在负权边的图。解决的问题大多是这样的：有一个无向图G(V,E)，边E[i]的权值为W[i]，找出V[0]到V[i]的最短路径。

4.2 算法思想

1）初始化：设定除源节点以外的其它所有节点到源节点的距离为inf(一个很大的数)，且这些节点都没被处理过。

2）从源节点出发，更新相邻节点到源节点的距离。然后在所有节点中选择一个最短距离的点作为当前节点。

3）标记当前节点为done(表示已经被处理过)，与步骤2类似，更新其相邻节点的距离。(这些相邻节点的距离更新也叫松弛，目的是让它们与源节点的距离最小。因为你是在当前最小距离的基础上进行更新的，由于当前节点到源节点的距离已经是最小的了，那么如果这些节点之前得到的距离比这个距离大的话，我们就更新它)。

4）步骤3做完以后，设置这个当前节点已被done，然后寻找下一个具有最小代价(cost)的点，作为新的当前节点，重复步骤3.

5)如果最后检测到目标节点时，其周围所有的节点都已被处理，那么目标节点与源节点的距离就是最小距离了。如果想看这个最小距离所经过的路径，可以回溯，前提是你在步骤3里面加入了当前节点的最优路径前驱节点信息。

4.3 dijkstra是广度优先搜索算法吗

不是，扩展表的进行方式和广度优先不同。只是某处有点类似广度优先搜索。Dijkstra是从起点出发，遍历其起点的节点，记录到各子节点的位置，选择一条权值小的路，然后从这个子节点出发，到其中一个子节点，计算其到起点的距离，比较从原点出发所得距离最小的那个节点（没有子节点的就不比较了），从那个节点出发。得到距离后再比较，再从最小的节点出发。（而广度优先搜索是要遍历完一个节点的每一个子节点，然后在遍历完子节点的子节点。而Dijkstra每次从已遍历到节点中到起点距离最小的那个节点出发）（把广度优先搜索的队列里的数据换成权值低的先出队列就是dijkstra了）

4.4 Dijkstra算法

//用的是临接矩阵，自身到自身的距离为0。

 1void dijkstra(int s,int t)

 2{

 3    bool vis[203];//标记该点是否访问过

 4    int dis[203];//保存最短路径

 5    int i, j, k;

 6

 7    for(i=0;i<n;i++)//初始化

 8        dis[i] =G[s][i];//s—>各个点的距离，未直接连接的为inf

 9    memset(vis,false,sizeof(vis));//初始化为假表示未访问过

10     dis[s] =0;//s->s距离为0

11     vis[s] =true;//s点访问过了，标记为真

12    for(i=1;i<n;i++)//G.V-1次操作+上面对s的访问 = G.V次操作

13    {

14         k =-1;

15        for(j=0;j//从尚未访问过的点中选一个距离最小的点

16            if(!vis[j] && (k==-1||dis[k]>dis[j]))//未访问过 && 是距离最小的（不会出现dis[-1]）

17                 k = j;

18        if(k == -1)//若图找不到则结束

19            break;//跳出循环

20         vis[k] =true;//将k点标记为访问过了（下面保证其周围所有的边都判断了）

21        for(j=0;j<n;j++)//松弛操作

22            if(!vis[j] && dis[j]>dis[k]+G[k][j])//该点未访问过 && 可以进行松弛

23                 dis[j] = dis[k]+G[k][j];//j点的距离 大于当前点的距离+w(k,j)则松弛成功，进行更新

24    }

25     printf("%d\n",dis[t]==MAX?-1:dis[t]);//输出结果

26 }

五、Floyd-Warshall算法（Floyd-Warshall algorithm）(动态规划)

是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N³)，空间复杂度为O(N²)。

5.1 算法描述

1)算法思想原理：

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）

从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j)< Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) +Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

2).算法描述：

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 　　

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w使得从 u 到 w再到 v 比己知的路径更短。如果是更新它。

3).Floyd算法过程矩阵的计算----十字交叉法

5.2 Floyd-Warshall的原理是动态规划

设Di,j,k为从i到j的只以(1..k)集合中的节点为中间节点的最短路径的长度。若最短路径经过点k，则Di,j,k = Di,k,k-1 + Dk,j,k-1；若最短路径不经过点k，则Di,j,k = Di,j,k-1。因此，Di,j,k = min(Di,k,k-1 +Dk,j,k-1 , Di,j,k-1)。

在实际算法中，为了节约空间，可以直接在原来空间上进行迭代，这样空间可降至二维。

5.3 floyd程序

1void floyd()

 2{

 3    int i, j, k;

 4

 5    for(k=0;k)

 6        for(i=0;i)

 7            for(j=0;j)

 8                 G[i][j] = min(G[i][j],G[i][k]+G[k][j]);

 9    printf("%d\n",G[s][t]==MAX?-1:G[s][t]);

10 }

这段代码的基本思想就是：最开始只允许经过0号顶点进行中转，接下来只允许经过0和1号顶点进行中转……允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点，只经过前k号点的最短路程。补充一下：对于floyd判断负环是否存在只需检查是否存在d[i][i]是负数的顶点i即可。

六、SPFA

是Bellman-Ford的队列优化，时效性相对好，时间复杂度O（kE），其中（k<与Bellman-ford算法类似，SPFA算法采用一系列的松弛操作以得到从某一个节点出发到达图中其它所有节点的最短路径。所不同的是，SPFA算法通过维护一个队列，使得一个节点的当前最短路径被更新之后没有必要立刻去更新其他的节点，从而大大减少了重复的操作次数。

6.1 SPFA算法：

设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止。SPFA在形式上和广度(宽度)优先搜索非常类似，不同的是bfs中一个点出了队列就不可能重新进入队列，但是SPFA中一个点可能在出队列之后再次被放入队列，也就是一个点改进过其它的点之后，过了一段时间可能本身被改进(重新入队)，于是再次用来改进其它的点，这样反复迭代下去。

6.2 SPFA是这样判断负环的

如果某个点进入队列的次数超过N次，则存在负环（SPFA无法处理带负环的图）。

6.3 SPFA适用场合

因为spfa是动态维护最短路，所以对于一个节点入队次数越少，他的时间复杂度就越小。也就是说，只要图越稀疏，spfa的时间复杂度就越低。所以，spfa适用于比较稀疏的图。在稠密图里spfa容易超时。spfa可以处理负权图，因为他是动态维护了最短路。所以用spfa时不需要考虑是否存在负边。spfa可以处理负环，需要注意的是，可以处理负环不代表他能求出有负环的图的最短路，他只是能判断是否存在负环。

与Dijkstra算法与Bellman-ford算法都不同，SPFA的算法时间效率是不稳定的，即它对于不同的图所需要的时间有很大的差别。在最好情形下，每一个节点都只入队一次，则算法实际上变为广度优先遍历，其时间复杂度仅为O(E)。另一方面，存在这样的例子，使得每一个节点都被入队(V-1)次，此时算法退化为Bellman-ford算法，其时间复杂度为O(VE)。

SPFA算法在负边权图上可以完全取代Bellman-ford算法，另外在稀疏图中也表现良好。但是在非负边权图中，为了避免最坏情况的出现，通常使用效率更加稳定的Dijkstra算法，以及它的使用堆优化的版本。通常的SPFA算法在一类网格图中的表现不尽如人意。

6.4 SPFA算法

 1bool SPFA()

 2{

 3    int u;//从队列que中取出的数

 4    int i;

 5    queue<int >que;//队列

 6    int dis[503];//保存最短距离

 7    bool vis[503];//标记是否访问过

 8    int flag[503];//记录点进入队列的次数

 9

10     memset(flag,0,sizeof(flag));//初始化为0

11     memset(vis,false,sizeof(vis));//初始化

12     fill(dis,dis+n+1,MAX);//初始化

13     dis[1] =0;//从1开始

14     que.push(1);//将 1 放入队列

15    while(!que.empty()){//队列不为空

16         u = que.front();//从队列中取出一个数

17         que.pop();//删除此数

18         vis[u] =false;//标记为未访问过

19        for(i=1;i<=n;i++)//对所有的边判断（采用临接矩阵存储的，若是临接表就可直接判断存在的边）

20        {

21            if(dis[i]>dis[u]+G[u][i]){//进行松弛

22                 dis[i] = dis[u]+G[u][i];//松弛成功

23                if(!vis[i]){//若点i未被访问过

24                     vis[i] =true;//标记为访问过

25                     flag[i]++;//入队列次数+1

26                    if(flag[i]>=n)//若此点进入队列此数超过n次 说明有负环

27                        return true;//有负环

28                     que.push(i);//将此点放入队列

29                }

30            }

31        }

32    }

33    return

            false;//没有负环

34 }

6.5 两个著名优化（SLF和LLL）

SPFA是按照 FIFO的原则更新距离的, 没有考虑到距离标号的作用. 实现中 SPFA 有两个非常著名的优化: SLF 和 LLL.

SPFA算法有两个优化算法 SLF和 LLL：

SLF：Small Label First策略，设要加入的节点是j，队首元素为i，若dist(j)< dist(i)，则将j插入队首，否则插入队尾。

LLL：LargeLabel Last策略，设队首元素为i，每次弹出时进行判断，队列中所有dist值的平均值为x，若dist(i)>x则将i插入到队尾，查找下一元素，直到找到某一i使得dist(i)<=x，则将i出对进行松弛操作。

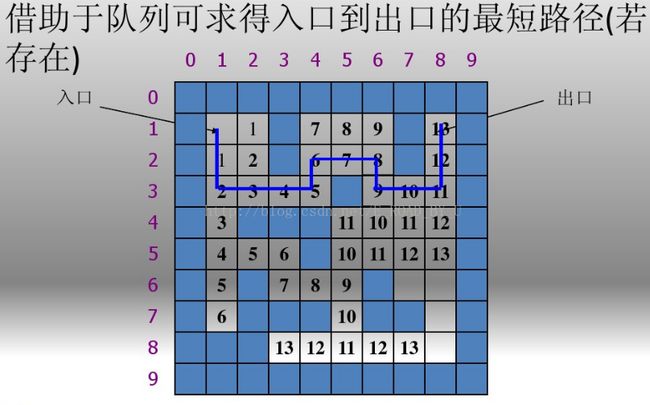
七、广度优先搜索

广度优先搜索算法（Breadth-First-Search），又译作宽度优先搜索，或横向优先搜索，简称BFS。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。广度优先搜索的实现一般采用open-closed表。

使用该算法注意的问题：

     （1）使用该算法关键的数据结构为：队列，队列保证了广度优先，并且每个节点都被处理到

     （2）新加入的节点一般要是未处理过的，所以某些情况下最初要对所有节点进行标记

利用队列保存没有寻找过的点，利用数组保存寻找过的节点的父节点，遍历完所有的节点后，由目的节点在数组中找其父节点，然后找父节点的父节点依次直到开始节点。

bfs求最短路：

1struct P

 2{

 3    int v, w;//v顶点 w最短距离

 4    bool operator <(const P &a)const{

 5        return a.w < w;//按w 从小到大排序

 6    }

 7};

8 priority_queue

que;//优先队列，按w从小到大

程序在另一篇博客中写过：http://blog.csdn.net/e_road_by_u/article/details/70037441

感觉广搜只能搜索权值不一样的二叉树或权值都一样的图。（因为广搜只能进一次队列）（如果使用优先队列则都可以，这时可以按照起点到当前搜到的点的权值进行排序，权值低的优先出队。这与dijstra不是一样了吗？？？）