《机器学习基石》9-Linear Regression

这一节主要介绍线性回归算法。

Linear Regression Problem

对于输出空间 Y=R Y = R 的一类问题，一个比较简单的想法就是：将 Linear Classification 的决策函数中的 sign 函数去掉，使用各种特征的加权结果来表示 y y

y≈∑i=0dwixi=wTx y ≈ ∑ i = 0 d w i x i = w T x

这就是线性回归算法，它的假设空间为

h(x)=wTx h ( x ) = w T x

线性回归的目标是寻找一条直线 （ R2 R 2 ） 或者一个平面 （ R3 R 3 ）或者超平面（ Rn R n ），使得误差最小，常用的误差函数是平方误差

Ein(w)=1N∑n=1N(h(xn)−yn)2 E i n ( w ) = 1 N ∑ n = 1 N ( h ( x n ) − y n ) 2

Eout(w)=ϵ(x,y)∼P(wTx−y) E o u t ( w ) = ϵ ( x , y ) ∼ P ( w T x − y )

Linear Regression Algorithm

将 Ein E i n 写成矩阵形式

Ein(w)=1N∑n=1N(h(xn)−yn)2=1N∥∥∥xT1w−y1xT2w−y2⋅⋅⋅xTNw−yN∥∥∥2=1N∥Xw−y∥2 E i n ( w ) = 1 N ∑ n = 1 N ( h ( x n ) − y n ) 2 = 1 N ‖ x 1 T w − y 1 x 2 T w − y 2 ⋅ ⋅ ⋅ x N T w − y N ‖ 2 = 1 N ‖ X w − y ‖ 2

其中

X=[xT1,1xT2,1⋅⋅⋅xTN,1]∈RN×(d+1) X = [ x 1 T , 1 x 2 T , 1 ⋅ ⋅ ⋅ x N T , 1 ] ∈ R N × ( d + 1 )

w∈R(d+1)×1 w ∈ R ( d + 1 ) × 1

y∈RN×1 y ∈ R N × 1

我们的目标是找到一个 w w ，使得 Ein(w) E i n ( w ) 尽可能小。因此，将 Ein(w) E i n ( w ) 对 w w 求导，得到：

∇Ein(w)=2NXT(Xw−y) ∇ E i n ( w ) = 2 N X T ( X w − y )

令 ∇Ein(w)=0 ∇ E i n ( w ) = 0 ，得到 w w 的最优解

wLIN=(XTX)−1XTy=X†y w LIN = ( X T X ) − 1 X T y = X † y

其中

X†=(XTX)−1XT X † = ( X T X ) − 1 X T

称为矩阵 X X 的伪逆，于是

h(x)=wTLINx h ( x ) = w LIN T x

将上面做一个小结，得到 Linear Regression 算法的流程如下：

Generalization Issue

下面我们来分析一下 Linear Regression 的 Ein E i n

Ein(wLIN)=1N||y−y^||2=1N||y−XX†y||2=1N||(I−H)y||2 E i n ( w L I N ) = 1 N | | y − y ^ | | 2 = 1 N | | y − X X † y | | 2 = 1 N | | ( I − H ) y | | 2

其中 H=XX† H = X X † 是投影矩阵，把 y y 投影到 X X 的 d+1 d + 1 个向量构成的平面上， H H 有如下的性质：

• 对称性 H=HT H = H T
• 幂等性 H2=H H 2 = H
• 半正定性 λi≥0 λ i ≥ 0
• trace(I−H)=N−(d+1) t r a c e ( I − H ) = N − ( d + 1 )

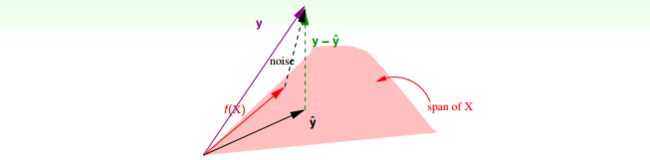
假设 y=f(X)+noise,f(x)∈span y = f ( X ) + noise , f ( x ) ∈ span ，那么如上图所示，有

Ein(wLIN)=1N||(I−H)y||2=1N||(I−H)noise||2=1Ntrace(I−H)||noise||2=1N(N−(d+1))||noise||2 E i n ( w L I N ) = 1 N | | ( I − H ) y | | 2 = 1 N | | ( I − H ) n o i s e | | 2 = 1 N t r a c e ( I − H ) | | n o i s e | | 2 = 1 N ( N − ( d + 1 ) ) | | n o i s e | | 2

得到：

Ein(wLIN)=||noise||2⋅(1−d+1N) E i n ( w L I N ) = | | n o i s e | | 2 ⋅ ( 1 − d + 1 N )

Eout(wLIN)=||noise||2⋅(1+d+1N) E o u t ( w L I N ) = | | n o i s e | | 2 ⋅ ( 1 + d + 1 N )

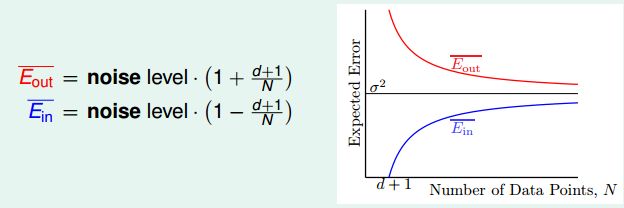
两者最终都向 σ2 σ 2 (noise level)收敛，差距是 2(d+1)N 2 ( d + 1 ) N ，因此说明算法是可行的。

Linear Regression for Binary Classification

对比一下 Linear Classification 与 Linear Regression：

• Linear Regression
  
  • 用于分类问题
  • Y={+1,−1} Y = { + 1 , − 1 }
  • h(x)=sign(wTx) h ( x ) = sign ( w T x )
  • NP-hard，难于求解
• Linear Regression
  
  • 用于回归问题
  • Y=R Y = R
  • h(x)=wTx h ( x ) = w T x
  • 易于求解

因为

err0/1=[[sign(wTx)≠y]]≤errsqr=(wTx−y)2 err 0 / 1 = [ [ sign ( w T x ) ≠ y ] ] ≤ err sqr = ( w T x − y ) 2

所以可以将 Linear Regression 用于分类问题上：

1. run Linear Regression on binary classification data D D
2. return g(x)=sign(wTLINx) g ( x ) = sign ( w LIN T x )

以上便是 Linear Regression 的内容。