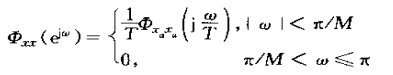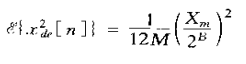《离散时间信号处理学习笔记》—连续时间信号的采样(四)
注:本博客是基于奥本海姆《离散时间信号处理》第三版编写,主要是为了自己学习的复习与加深。
一、在A/D和D/A转换中的过采样和噪声形成
一)、采样直接量化的过采样A/D转换
1、为了研究过采样和量化阶大小之间的关系,考虑图4.1所示的系统。
为了分析过采样在该系统中的效果,考虑一个零均值广义平稳的随机过程xa(t),其功率谱密度记为![]() ,自相关函数记为
,自相关函数记为![]() 。为了简化讨论,最初假设xa(t)已经带限到Ωn,即
。为了简化讨论,最初假设xa(t)已经带限到Ωn,即
并且假定![]() ,常数M为zhengs称为过采样。
,常数M为zhengs称为过采样。
2、利用加性噪声模型,能用图4.2图带图4.1.图4.2中的抽取滤波器是增益为1,截止频率为wc=π/M的理想低通滤波器。
因为图4.2所示的整个系统是线性的,所以它的输出xd[n]由两个分量:一个忧郁输入信号xa(t)引起的,另一个忧郁量化噪声e[n]产生的,分别记为![]() 。
。
3、目的是要输出xd[n]中确定作为量化阶△和过采样M的函数的信号功率![]() 对量化噪声功率
对量化噪声功率![]() 的比。因为图4.2所示的系统是线性的,且假定噪声与信号不相关,所以在计算输出终端和噪声分量各自的功率时可以作为两个源来对待
的比。因为图4.2所示的系统是线性的,且假定噪声与信号不相关,所以在计算输出终端和噪声分量各自的功率时可以作为两个源来对待
1)、输出中的信号量。先将采样信号x[n]的功率谱密度、自相关函数和信号功率与梁旭时间模拟信号xa(t)的对应函数联系起来。令![]() 分别记为x[n]的自相关函数和功率密度浦,那么按照定义就有
分别记为x[n]的自相关函数和功率密度浦,那么按照定义就有![]() ,由于
,由于![]() 于是
于是
![]() 式4.2
式4.2
因此
也就是说,样本序列的自相关函数就是对应的连续时间信号自相关函数的采样。特别是,广义平稳的假定就意味着![]() 是一个独立于t的常数。这样就得到
是一个独立于t的常数。这样就得到
因为功率密度谱是自相关函数的博里叶变换,作为式4.3的结果,由
假设输入是带限的,如式4.5,有假设过采样M倍,从而有2π/T=2MΩn,将Ω=w/T带入4式4.5可得
若![]() 如图4.3(a)所示,而选取的采样率尤为
如图4.3(a)所示,而选取的采样率尤为![]() 那么
那么![]() 就一定如图4.3(b)所示。
就一定如图4.3(b)所示。
2)、量化产生的噪声分量。假设e[n]是一个广义平稳的白噪声过程,其均值为零,方差为
结果,e[n]的自相关函数和功率谱密度分别为
和
图4.4示出了e[n]和x[n]的功率密度谱。
量化信号![]() 的功率密度普就是这两者之和。
的功率密度普就是这两者之和。
3、随着过采样率M的增加,量化噪声与信号谱重叠的分量就减少。正式这种过采样的效果才使得信号对量化噪声比得以改善。具体地说,该理想低通滤波器在频带π/M<|w|≤π内消除量化噪声,而信号分量没有改变,理想低通滤波器输出端的噪声功率为
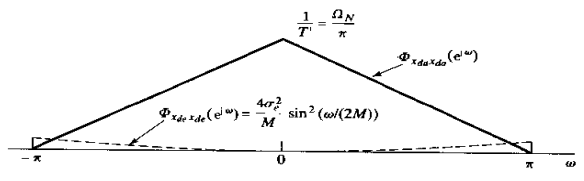
接下来,低通过滤后的信号被减采样。已经知道在减采样输出中信号功率未变。图4.5表示了xda[n]和xde[n]的功率密度普。
将图4.4和图4.5比较可见,因为频率轴和幅度轴的尺度变换是相反的,所以信号功率密度普下的面积没有变换。另一方面,在抽取输出中的噪声功率和低通滤波器输出中是相同的,即
因此,通过滤波和减采样,量化噪声![]() 已减小了M倍,而信号功率依旧未变。
已减小了M倍,而信号功率依旧未变。
4、对于式4.11可知,对于某一给定的量化噪声功率,过采样因子M和量化器△之间明显有一个权衡。对于一个(B+1)位的量化器,最大输入信号电平在正负Xm之间,其量化阶为
和
式4.13说明,对于某一固定的量化器,其提高过采样比M能将噪声功率减小。因为信号功率与M无关,所以增加M就会使信号对量化噪声值比增加。换句话说,对于某一固定的量化噪声功率![]() ,所需要的B值为
,所需要的B值为
由上式可见,为达到某一给定的信号量量化噪声比,美当过采样比M加倍,量化位数可减少1/2位;或者换句话说,若过采样按因子M=4,在表示该信号为达到所期望的精度要求时可以减少1位。
二)、采用噪声成形的过采样A/D转换
1、噪声成形的基本思想是要改变A/D转换过程,以使得量化噪声的功率谱密度不再是均匀的,而是被成形为大部分噪声功率位于频带|w|<π/M之外的形式。这样一来,后续的滤波和减采样就将更多的量化噪声功率滤除。
2、噪声成形量化器如图4.6所示
图4.6(a)所示的方框图说明了这个系统是如何用继承电路实现的。图4.6(a)所示的系统可以用图4.6(b)所示的离散时间等效系统来表示。
3、将量化噪声用一个加性噪声源建模,从而,图4.6所示的系统就能用图4.7所示的线性模型来代替。在该系统中,输出y[n]是两个分量之和;单独有输入x[n]产生的yx[n]和单独有噪声e[n]产生的![]() 。
。
从x[n]到y[n]的传递函数记为Hx[z],从e[n]到y[n]的传递函数记为He[z]。这两个传递函数都能直接计算为
![]() 式4.15
式4.15
![]() 式4.16
式4.16
结果
和
因此,输出y[n]可等效地表示为y[n]=x[n]+![]() ,其中x[n]没有变化,而量化噪声e[n]则按一阶差分算子He[z]改变,这就如图4.8所示
,其中x[n]没有变化,而量化噪声e[n]则按一阶差分算子He[z]改变,这就如图4.8所示
利用式4.9给出的e[n]的功率谱密度,出现在y[n]中的量化噪声![]() 的功率密度普密度为
的功率密度普密度为
图4.9示出了![]() 的功率谱密度,e[n]的共飞利浦,以及曾示于图4.3(b)和图4.4的同一信号的功率谱。
的功率谱密度,e[n]的共飞利浦,以及曾示于图4.3(b)和图4.4的同一信号的功率谱。
4、在图4.6所示的系统中,带外的噪声功率被低通滤波器滤除。具体的说,图4.10示出了重叠在![]() 功率谱密度上的
功率谱密度上的![]() 功率普密度。
功率普密度。
因为减采样器并没有减少任何信号功率,所以在xda[n]中的信号功率为
在最后输出中的量化噪声功率为
为了与之前的结果近似地比较,假设M足够大,以至于满足
利用这一近似式,容易计算出式4.21为
通过式4.23再次看到,过采样率M和量化阶△之间有一个权衡。因此,对于一个(b+1)位的量化器和最大输入信号电平位于
![]() 之间,为了实现某一给定的量化噪声功率Pde,必须有
之间,为了实现某一给定的量化噪声功率Pde,必须有
比较式4.14和式4.24可见,不像直接量化一样,每次将过采样比M加倍,在量化上只有1/2比特的收益,而是利用噪声形成后由1.5比特的获益。
5、通过吸收进第2个累加器,可以将图4.6所示的噪声成形策略进一步推广,如图4.11所示。
在这种情况下,量化器还用加性噪声源e[n]建模,可以证明
![]()
式中,在两级的情况下,![]() 是经由传递函数
是经由传递函数
![]() 式子4.25
式子4.25
处理量化噪声e[n]的结果。对应的存在于y[n]中的量化噪声功率普密度为
![]() 式4.26
式4.26
有了这个结果,虽然两级噪声成形系统的输出总噪声功率比一级的情况还要大,但更多的噪声位于信号带宽之外。更一般得说,采用p级累加和反馈,相应的噪声成形为
![]() 式4.27
式4.27
三)、在D/A转换中的过采样和噪声成形
1、D/A转换的基本系统如图4.12所示,它是与图4.1所示的系统相对应。
要被转换为连续时间信号的序列yd[n]首先被增采样得到![]() ,然后再将其送到D/A转换器之前重新量化,这样D/A转换器所接收的二进制样本是用再量化过程所产生的位数。如果可以确保量化噪声不占据信号频带,那么就能用一个很少位数的简单D/A转换器,这样噪声就能用廉价的模拟滤波滤除。
,然后再将其送到D/A转换器之前重新量化,这样D/A转换器所接收的二进制样本是用再量化过程所产生的位数。如果可以确保量化噪声不占据信号频带,那么就能用一个很少位数的简单D/A转换器,这样噪声就能用廉价的模拟滤波滤除。
2、图4.13示出一种结构,其中量化器将量化噪声按照4.1所示系统提供的一阶噪声成形的类似方式。
为了分析图4.12和图4.13所示的系统,将图4.13中的量化器用一个加性白噪声源e[n]代替,这样就有了图4.14
从![]() 到y[n]的传递函数为1,也就是说,出现在输出端的增采样信号
到y[n]的传递函数为1,也就是说,出现在输出端的增采样信号![]() 没有变化。从e[n]到y[n]的传递函数He[z]为
没有变化。从e[n]到y[n]的传递函数He[z]为
![]() 式4.28
式4.28
因此图4.14中出现在噪声成形系统输出端的量化噪声分量![]() 具有功率密度普为
具有功率密度普为
![]() 式4.29
式4.29
式中,![]()
3、在实际装置中,总希望避免截止的模拟重构滤波器,如果能够容许少许多一点的量化噪声,那么D/C重构滤波器就不必如此陡峭地滚降。再者,若在噪声成形中采样多级处理,输出噪声功率谱就具有如下形式
![]() 式4.30
式4.30
这将会把更多的噪声推到更高的频率上,这时模拟重构滤波器的要求就能进一步方宽。