层次聚类之AGNES及Python实现

层次聚类

层次聚类，顾名思义，就是一层一层的进行聚类，它试图在不同层次对数据集进行划分，可以由上向下把大的类别分割，即“自顶向下”的分拆策略(见下面AGNES部分)，也可以由下向上对小的类别进行聚合，即“自底向下”的聚合策略：开始把所有的样本都归为一类，然后逐步将他们划分为更小的单元，直到最后每个样本都成为一类。在这个迭代的过程中通过对划分过程中定义一个松散度，当松散度最小的那个类的结果都小于一个阈值，则认为划分可以终止。这种方法用的不普遍，在这里不予详细介绍。下面本文主要对采用自底向上聚合策略的AGNES（AGglomerative NESting）做一个介绍。

AGNES

AGNES，是一种采用自底向上聚合策略的层次聚类算法，是先将数据集中的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数，这里的关键是如何计算聚类簇之间的距离。其实每个聚类簇就是一个样本集合，聚类簇之间的聚类就是集合之间的聚类。

簇直接的距离

最小距离，是由两个簇的最近样本决定。如果层次聚类的距离度量函数采用 dmin d m i n ，两个簇之间的相似度由两个簇中最近样本决定，这样容易造成Chaining的效果，即两个簇明明从“大局”上离得比较远，但是由于其中个别点的距离比较近就被合并了，并且这样合并之后Chaining效应会进一步扩大，最后会得到比较松散的簇。

dmin(Ci,Cj)=minx∈Ci,z∈Cjdist(x,z)(1.1) (1.1) d m i n ( C i , C j ) = m i n x ∈ C i , z ∈ C j d i s t ( x , z )

python代码实现：

#计算欧几里得距离,a,b分别为两个元组
def dist(a, b):
    return math.sqrt(math.pow(a[0]-b[0], 2)+math.pow(a[1]-b[1], 2))

#dist_min
def dist_min(Ci, Cj):
    return min(dist(i, j) for i in Ci for j in Cj)

最大距离，由两个簇的最远样本决定。这个则是最小距离 dmin d m i n 的反面极端，其效果也是刚好相反的，限制非常大，两个 cluster 即使已经很接近了，但是只要有不配合的点存在，就顽固到底，老死不相合并，也是不太好的办法。 dmin d m i n 和 dmax d m a x 这两种相似度的定义方法的共同问题就是指考虑了某个有特点的数据，而没有考虑类内数据的整体特点。

dmax(Ci,Cj)=maxx∈Ci,z∈Cjdist(x,z)(1.2) (1.2) d m a x ( C i , C j ) = m a x x ∈ C i , z ∈ C j d i s t ( x , z )

python代码实现：

#dist_max
def dist_max(Ci, Cj):
    return max(dist(i, j) for i in Ci for j in Cj)

平均距离，由两个簇所有样本共同决定。就是把两个集合中的点两两的距离全部放在一起求一个平均值，相对也能得到合适一点的结果。有时异常点的存在会影响均值，平常人和富豪平均一下收入会被拉高是吧，因此这种计算方法的一个变种就是取两两距离的中位数

davg(Ci,Cj)=1|Ci||Cj|∑x∈Ci∑x∈Cjdist(x,z)(1.3) (1.3) d a v g ( C i , C j ) = 1 | C i | | C j | ∑ x ∈ C i ∑ x ∈ C j d i s t ( x , z )

python代码实现：

#dist_avg
def dist_avg(Ci, Cj):
    return sum(dist(i, j) for i in Ci for j in Cj)/(len(Ci)*len(Cj))

算法过程（摘抄于周志华的《机器学习》）

AGNES算法描述如下所示，在第1-9行，算法先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化；然后在第11-23行，AGNES不断合并最近的聚类簇，并对合并得到的聚类簇的距离矩阵进行更新；上述过程不断重复，直至达到预设的聚类簇数。

---

输入：样本集 D={x1,x2,...,xm} D = { x 1 , x 2 , . . . , x m }
   聚类簇距离度量函数 d d ；
   聚类簇数 k k
过程：
1. for j=1,2,...,m j = 1 , 2 , . . . , m do
2.   Cj={xj} C j = { x j }
3. end for
4. for i=1,2,...,m i = 1 , 2 , . . . , m do
5.  for i=1,2,...,m i = 1 , 2 , . . . , m do
6.    M(i,j)=d(Ci,Cj) M ( i , j ) = d ( C i , C j ) ;
7.    M(j,i)=M(i,j) M ( j , i ) = M ( i , j ) ;
8.  end for
9. end for
10. 设置当前聚类簇个数： q=m q = m ;
11. while q>k q > k do
12.  找出距离最近的两个聚类簇 Ci∗ C i ∗ 和 Cj∗ C j ∗ ;
13.  合并 Ci∗ C i ∗ 和 Cj∗ C j ∗ ： Ci∗=Ci∗⋃Cj∗ C i ∗ = C i ∗ ⋃ C j ∗ ；
14.  for j=j∗+1,j∗+2,..,q j = j ∗ + 1 , j ∗ + 2 , . . , q do
15.   将聚类簇 Cj C j 重新编号为 Cj C j
16.  end for
17.  删除距离矩阵 M M 的第 j∗ j ∗ 行和第 j∗ j ∗ 列;
18.  for j=1,2,...,q−1 j = 1 , 2 , . . . , q − 1 do
19.    M(i,j)=d(Ci,Cj) M ( i , j ) = d ( C i , C j ) ;
20.    M(j,i)=M(i,j) M ( j , i ) = M ( i , j ) ;
21.  end for
22.   q=q−1 q = q − 1
23. end while
输出：簇划分: C={C1,C2,...,Ck} C = { C 1 , C 2 , . . . , C k }

---

python代码实现：

def AGNES(dataset, dist, k):
    #初始化C和M
    C = [];M = []
    for i in dataset:
        Ci = []
        Ci.append(i)
        C.append(Ci)
    for i in C:
        Mi = []
        for j in C:
            Mi.append(dist(i, j))
        M.append(Mi)
    q = len(dataset)
    #合并更新
    while q > k:
        x, y, min = find_Min(M)
        C[x].extend(C[y])
        C.remove(C[y])
        M = []
        for i in C:
            Mi = []
            for j in C:
                Mi.append(dist(i, j))
            M.append(Mi)
        q -= 1
    return C

AGNES实例

完整代码见Github.

数据集

#数据集：每三个是一组分别是西瓜的编号，密度，含糖量
data = """
1,0.697,0.46,2,0.774,0.376,3,0.634,0.264,4,0.608,0.318,5,0.556,0.215,
6,0.403,0.237,7,0.481,0.149,8,0.437,0.211,9,0.666,0.091,10,0.243,0.267,
11,0.245,0.057,12,0.343,0.099,13,0.639,0.161,14,0.657,0.198,15,0.36,0.37,
16,0.593,0.042,17,0.719,0.103,18,0.359,0.188,19,0.339,0.241,20,0.282,0.257,
21,0.748,0.232,22,0.714,0.346,23,0.483,0.312,24,0.478,0.437,25,0.525,0.369,
26,0.751,0.489,27,0.532,0.472,28,0.473,0.376,29,0.725,0.445,30,0.446,0.459"""

实验结果

采用 davg d a v g 运行结果

采用 dmin d m i n 运行结果

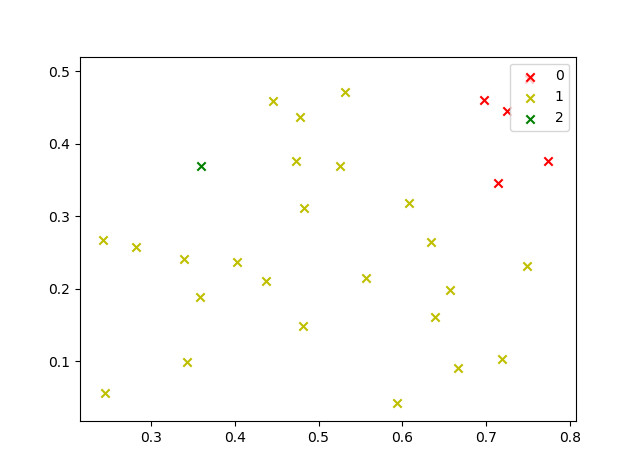
采用 dmax d m a x 运行结果

---

更多机器学习干货、最新论文解读、AI资讯热点等欢迎关注”AI学院(FAICULTY)”
欢迎加入faiculty机器学习交流qq群：451429116 点此进群
版权声明：可以任意转载，转载时请务必标明文章原始出处和作者信息.

---

参考文献

[1]. 周志华，机器学习，清华大学出版社，2016
[2]. 聚类算法——python实现层次聚类（AGNES）