数据结构与算法-快速排序
概要
- 快速排序是冒泡排序的升级版
- 基本思想
- java代码实现
- 图示代码执行过程
- 进一步优化1:优化选取枢轴
- 进一步优化2:优化不必要的交换
- 进一步优化3:优化小数组时的排序方案
- 进一步优化4:优化递归操作
- 算法复杂度分析
快速排序是冒泡排序的升级版
快速排序和冒泡排序都属于交换类排序。即它也是通过不断比较和移动交换来实现排序的,只不过它的实现,增大了记录的比较和移动的距离,将关键字较大的记录从前面直接移动到后面,关键字较小的记录从后面直接移动到前面,从而减少了总的比较次数和移动交换次数。
基本思想
快速排序(Quick Sort)的基本思想是:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序的目的。
java代码实现
/**
* 交换数组中的两个元素
*
* @param a 数组
* @param from 元素一的下标
* @param to 元素二的下标
*/
void swap(int[] a, int from, int to) {
int temp = a[from];
a[from] = a[to];
a[to] = temp;
}
/**
* 将待排序列分成以某枢轴分割的两个有序子序列
* 第一个子序列所有关键字均小于枢轴,第二个子序列所有关键字均大于枢轴
* {5,1,9,3,7,4,8,6,2} 取5为枢轴=> {2,1,4,3,5,7,8,6,9}
*
* @param a 待排序列
* @param low 序列起始地址
* @param high 序列结束地址
* @return
*/
int partition(int[] a, int low, int high) {
int pivotkey;
pivotkey = a[low]; /* 用子表的第一个记录作枢轴记录 */
while (low < high) { /* 从表的两端交替向中间扫描 */
while (low < high && a[high] >= pivotkey) {
high--;
}
swap(a, low, high); /* 将比枢轴记录小的记录交换到低端 */
while (low < high && a[low] <= pivotkey) {
low++;
}
swap(a, low, high); /* 将比枢轴记录大的记录交换到高端 */
}
return low; /* 返回枢轴所在位置 */
}
/**
* 快速排序(Quick Sort)
*
* @param a 待排序列
* @param low 序列起始地址
* @param high 序列结束地址
*/
void quickSort(int[] a, int low, int high) {
int pivot;
if (low < high) {
pivot = partition(a, low, high); /* 将待排序列一分为二,并算出枢轴值pivot */
quickSort(a, low, pivot); /* 对低子表递归排序 */
quickSort(a, pivot+1, high); /* 对高子表递归排序 */
}
}
//声明待排序列
int[] a = {5,1,9,3,7,4,8,6,2};
//测试调用
quickSort(a, 0, 8); //输出1,2,3,4,5,6,7,8,9
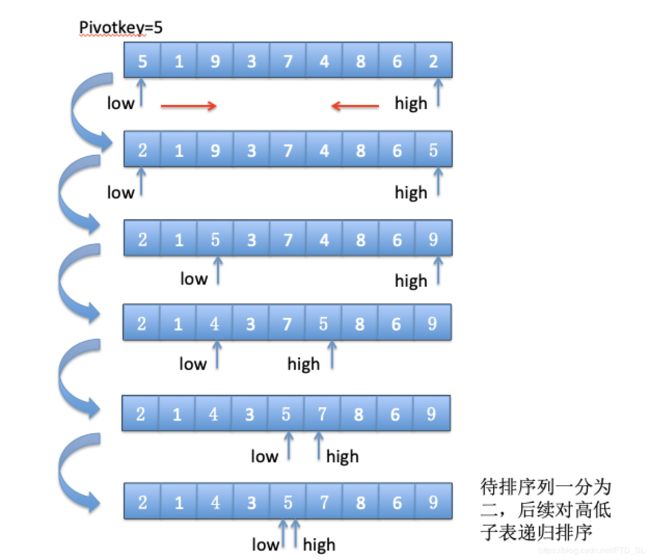
图示代码执行过程
进一步优化1:优化选取枢轴
分析代码pivotkey = a[low],固定选取第一个关键字作为首个枢轴是一个潜在的性能瓶颈。排序速度的快慢取决于枢轴处在整个序列中的位置,枢轴太小或太大,都会影响性能。于是就有了**三数取中(median-of-three)法。即取三个关键字先进行排序,将中间数作为枢轴,一般是取左端、右端和中间三个数,**也可以随机选取。这样至少这个中间数一定不会是最小或者最大的数,从概率来说,取三个数均为最小或最大的可能性是微乎其微的,因此中间数位于较为中间的值的可能性就大大提高了。由于整个序列是无序状态,随机选取三个数和从左中右端取三个数其实是一回事,而且随机数生成器本身还会带来时间上的开销,因此随机生成不予考虑。
/**
* 将待排序列分成以某枢轴分割的两个有序子序列
* 第一个子序列所有关键字均小于枢轴,第二个子序列所有关键字均大于枢轴
* {5,1,9,3,7,4,8,6,2} 取5为枢轴=> {2,1,4,3,5,7,8,6,9}
*
* @param a 待排序列
* @param low 序列起始地址
* @param high 序列结束地址
* @return
*/
int partition(int[] a, int low, int high) {
int pivotkey;
/* 三数取中法选枢轴 */
int mid = low+(high-low)/2; /* 计算数组中间的元素下标 */
if (a[low] > a[high]) {
swap(a, low, high); /* 交换左端和右端数据,保证左端较小 */
}
if (a[mid] > a[high]) {
swap(a, mid, high); /* 交换中间和右端数据,保证中间较小 */
}
if (a[low] < a[mid]) {
swap(a, low, mid); /* 交换左端和中间的数据,保证左端较小 */
}
/* 此时,a[low]已经成为整个序列左中右三个关键字的中间值 */
pivotkey = a[low]; /* 用子表的第一个记录作枢轴记录 */
while (low < high) { /* 从表的两端交替向中间扫描 */
while (low < high && a[high] >= pivotkey) {
high--;
}
swap(a, low, high); /* 将比枢轴记录小的记录交换到低端 */
while (low < high && a[low] <= pivotkey) {
low++;
}
swap(a, low, high); /* 将比枢轴记录大的记录交换到高端 */
}
return low; /* 返回枢轴所在位置 */
}
进一步优化2:优化不必要的交换
/**
* 将待排序列分成以某枢轴分割的两个有序子序列
* 第一个子序列所有关键字均小于枢轴,第二个子序列所有关键字均大于枢轴
* {5,1,9,3,7,4,8,6,2} 取5为枢轴=> {2,1,4,3,5,7,8,6,9}
*
* @param a 待排序列
* @param low 序列起始地址
* @param high 序列结束地址
* @return
*/
int partition(int[] a, int low, int high) {
int pivotkey;
int temp; /* 申明一个临时存储空间 */
/* 三数取中法选枢轴 */
pivotkey = a[low]; /* 用子表的第一个记录作枢轴记录 */
temp = pivotkey; /* 将枢轴关键字备份到temp中 */
while (low < high) { /* 从表的两端交替向中间扫描 */
while (low < high && a[high] >= pivotkey) {
high--;
}
a[low] = a[high]; /* 采用替换而不是交换的方式进行操作 */
while (low < high && a[low] <= pivotkey) {
low++;
}
a[high] = a[low]; /* 采用替换而不是交换的方式进行操作 */
}
a[low] = temp; /* 将枢轴数值替换回a[low] */
return low; /* 返回枢轴所在位置 */
}
我们这边申明一个临时存储空间temp,然后在之前是swap时,只作替换的工作,最终当low与high会和,即找到枢轴的位置时,再将temp的数值赋值回a[low]。因为这当中少了多次交换数据的操作,在性能上又得到了部分的提高。
进一步优化3:优化小数组时的排序方案
如果待排序列非常小,则快速排序反而不如直接插入排序来得更好(直接插入是简单排序中性能最好的)。其原因在于快速排序用到了递归操作,在大量数据排序时,这点性能影响相对于它的整体算法优势而言是可以忽略的,但如果数组只有几个记录需要排序时。这就成了一个大炮打蚊子的大问题。
/**
* 快速排序(Quick Sort)
*
* @param a 待排序列
* @param low 序列起始地址
* @param high 序列结束地址
*/
void quickSort(int[] a, int low, int high) {
int MAX_LENGTH_SORT = 7; /* 数组长度阀值 */
int pivot;
if ((high-low) > MAX_LENGTH_SORT) { /* 当high-low大于阀值时用快速排序 */
pivot = partition(a, low, high); /* 将待排序列一分为二,并算出枢轴值pivot */
quickSort(a, low, pivot); /* 对低子表递归排序 */
quickSort(a, pivot+1, high); /* 对高子表递归排序 */
} else { /* 当high-low小于等于阀值时用直接插入排序 */
insertSort(a);
}
}
进一步优化4:优化递归操作
大家知道,递归对性能是有一定影响的,quickSort函数在其尾部有两次递归操作。如果待排序的序列划分极端不平衡,递归深度将趋近于n,而不是平衡的log2n,这样就不仅仅是速度快慢的问题了。栈的大小是很有限的,每次递归调用都会耗费一定的栈空间,函数的参数越多,每次递归耗费的空间也越多。因此如果能减少递归,将会大大提高性能。
/**
* 快速排序(Quick Sort)
*
* @param a 待排序列
* @param low 序列起始地址
* @param high 序列结束地址
*/
void quickSort(int[] a, int low, int high) {
int MAX_LENGTH_SORT = 7; /* 数组长度阀值 */
int pivot;
if ((high-low) > MAX_LENGTH_SORT) { /* 采用快速排序 */
pivot = partition(a, low, high); /* 将待排序列一分为二,并算出枢轴值pivot */
quickSort(a, low, pivot); /* 对低子表递归排序 */
/* 采用迭代而不是递归,缩减堆栈深度,提高整体性能 */
low = pivot+1;
} else { /* 采用直接插入排序 */
insertSort(a);
}
}
算法复杂度分析
- 最优情况下,partition函数每次都划分得很均匀,如果排序n个关键字,其递归树的深度就为log2n向下取整+1,即仅需递归log2n次,加上比较的次数,其时间复杂度为O(nlogn)。
- 最坏的情况下,待排序的序列为正序或逆序,每次划分只得到一个比上一次划分少一个记录的子序列,注意另一个为空。如果递归树画出来,它就是一颗斜树。此时需要执行n-1次递归调用,且第i次划分需要经过n-i次关键字比较才能找到第i个记录,也就是枢轴的位置,因此最终其时间复杂度为0(n2 )。
- 就空间复杂度来说,主要是递归造成的栈空间的使用,最好情况,递归树的深度为log2n,其空间复杂度也就为0(logn),最坏情况,需要进行n-1次递归调用,其空间复杂度为0(n)。
- 总的来说,快速排序的平均时间复杂度为O(nlogn),平均空间复杂度为0(logn),且由于关键字的比较和交换是跳跃进行的,因此快速排序是一种不稳定的排序方法。