线段树（Segment Tree）简介

基本概念

线段树（segment tree）是一种二叉搜索树，它的每一个结点对应着一个区间[l,r],叶子结点对应的是一个单位区间，即l==r。对于一个非叶子结点[l,r]，它的左儿子所表示的区间为[l,(l+r)/2],右儿子表示的区间为[(l+r)/2+1,r]。根据定义，线段树是一颗平衡二叉树，它的叶子结点的数目为N，即整个区间的长度。

例如，区间[1,10]的线段树如下图所示：

由于线段树是一颗平衡二叉树，所以它的高度为 log 级别，这是线段树时间复杂度良好的基础。

线段树的用途较广，主要用于更新和查询。这里的更新和查询一般至少有一个是指区间的更新或查询。由于更新和查询的方法种类比较多，这也决定了线段树的灵活性，针对不同的问题，线段树处理的方式不尽相同。

---

直接看例子

维护一个数列，每次进行两种操作：

1.修改一个元素（ O(log) 维护相关结点 ）
2.查询一段区间的最大值（ O(log) 查询相关结点的信息 ）

这是一个经典的RMQ(range minimum/maximum query)问题，用线段树该如何解决？这里更新是点更新，查询是区间查询。

基本操作（单点修改）

可以首先对原序列建立一颗线段树，然后对于更新操作，则对线段树的相应结点进行更新，对于查询操作则进行查询。具体操作如下：

建树（ O(n) ）：每个节点维护节点所代表区间的左右端点和该区间的信息（上面例子里就是最值）。建树时，如果到了叶子结点，那么这个结点的最值信息就是对应位置数组中的该元素值，否则递归地建左子树和右子树，然后将当前结点的区间最值设置为自己左子树和右子树的较优最值（即要维护的数据）。由于每个结点仅计算了一次，因此时间复杂度为O(n)。上面的方法是到叶子节点读入数据，自底向上递推的；当然还有一种方法是每读入一个元素x后执行修改操作 A[i]=x ，则时间复杂度为 O(nlogn) 。

修改（ O(logn) ）：一样递归调用，从根节点开始递归到叶子结点并修改叶子结点。回溯时对路径上相应结点的最值进行更新。可以证明，其只会影响 log(n) 个结点。

查询（ O(logn) ）：还是递归调用。从根节点开始递归查询，如果查询区间在该节点的左子树内，则查询左子树；如果在右子树内，则查询右子树；否则，查询左子树相应区间和右子树相应区间，并将两者的返回值信息（上面例子里就是较大值）返回。

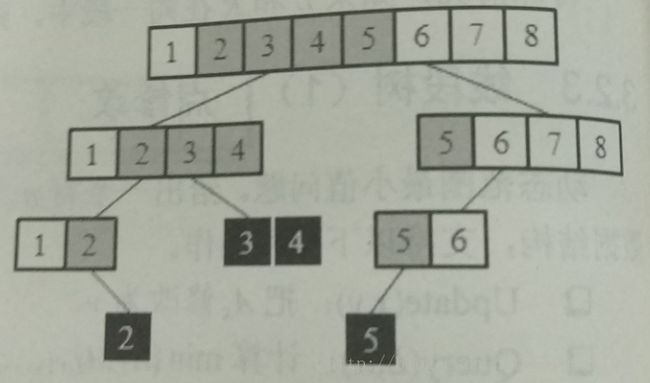
区间查询实际上是定位区间左右边界的操作，我们从根节点开始自顶向下找到待查询线段的左边界和右边界，则夹在中间的所有那些叶子节点不重复不遗漏地覆盖了整个待查询线段。如下图所示：

对于区间查询有一个结论：任意区间都能分解成不超过2h个不相交区间的并（这里h为线段树的最大深度）

从上图中不难发现，树的左右各有一条”主线”，虽有分叉，但每层最多只有两个支路向下延伸，因此查询边界结点不超过2h个。这实际上把待查询的线段分解成了不超过2h个不相交线段的并。也就证明了其时间复杂度是 O(logn) 级别的。

基本操作实现

单点加减 询问区间和

#include
#include
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
const int maxn=200010;

int sum[maxn<<2];

void PushUp(int rt){
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}

void build(int l,int r,int rt){
    if(l==r){
        scanf("%d",&sum[rt]);
        return ;
    }
    int m=(l+r)>>1;
    build(lson); build(rson);
    PushUp(rt);
}

void update(int p,int add,int l,int r,int rt){
    if(l==r){
        sum[rt]+=add;//这里是加减
        return ;
    }
    int m=(l+r)>>1;
    if(p<=m) update(p,add,lson);
    else update(p,add,rson);
    PushUp(rt);
}

int query(int L,int R,int l,int r,int rt){
    if(L<=l&&r<=R) return sum[rt];
    int m=(l+r)>>1;
    int ret=0;
    if(L<=m) ret+=query(L,R,lson);//这里是求和，也可以维护最值
    if(R>m) ret+=query(L,R,rson);
    return ret;
}

---

单点覆盖 询问区间最值

#include
#include
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
const int maxn=200010;

int maxx[maxn<<2];

void PushUp(int rt){
    maxx[rt]=max(maxx[rt<<1],maxx[rt<<1|1]);
}

void build(int l,int r,int rt){
    if(l==r){
        scanf("%d",&maxx[rt]);
        return ;
    }
    int m=(l+r)>>1;
    build(lson); build(rson);
    PushUp(rt);
}

void update(int p,int cov,int l,int r,int rt){
    if(l==r){
        maxx[rt]=cov;//这里是赋值
        return ;
    }
    int m=(l+r)>>1;
    if(p<=m) update(p,cov,lson);
    else update(p,cov,rson);
    PushUp(rt);
}

int query(int L,int R,int l,int r,int rt){
    if(L<=l&&r<=R) return maxx[rt];
    int m=(l+r)>>1;
    int ret=0;//较小数
    if(L<=m) ret=max(ret,query(L,R,lson));
    if(R>m) ret=max(ret,query(L,R,rson));
    return ret;
}

---

打标记操作（区间修改）

上面介绍的是支持点修改和区间查询的线段树。事实上，我们还会遇见一类问题是对区间的修改，经过“打标记”这种操作，线段树也是支持的。

对于区间修改，如果还用点修改的思想，那么每一修改在最坏的情况下会影响到树上的所有节点，这在时间上是不可接受的。

这时候我们想到线段树每个结点维护的就是区间的信息，现在我们要对区间内所有的数据进行修改，可不可以转为对区间结点的修改呢？（可是点修改就是这样做的呀(⊙o⊙)…，递归递归找到要修改的点，再pushup从新维护区间结点）。

当然我们要换一种思路了，这里打标记操作和点修改的区别是，只修改对应区间，先不修改点！（那后面的查询，万一要查询到前面修改的点，你没修改那个叶子，不就错了吗？(⊙o⊙)…） 所以我们不仅要打标记（只修改对应区间），还要在询问和再次修改时，将标记pushdown，即真正向下继续修改，也叫放标记。当标记放到叶子，就真正完成了修改。（当然可能永远放不到）。

由前面的结论，任意区间都能分解成不超过2h个不相交区间的并。因此每次区间修改的复杂度为 O(h) ，h为线段树的最大深度。

如果说区间查询是线段树所天生的肉体，那区间修改可以说是它的灵魂。

打标记操作实现

区间加减 询问区间和（区间最值同理）

#include
#include
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
const int maxn=200010;
typedef long long LL;

LL add[maxn<<2];//兼顾lazy标记与具体变化
LL sum[maxn<<2];

void PushUp(int rt){
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}

void PushDown(int rt,int len){
    if(add[rt]){
        add[rt<<1]+=add[rt];//下放，注意是+=而不是直接赋值
        add[rt<<1|1]+=add[rt];
        sum[rt<<1]+=add[rt]*(len-(len>>1));
        sum[rt<<1|1]+=add[rt]*(len>>1);
        add[rt]=0;//下放了，清除标记
    }
}

void build(int l,int r,int rt){
    add[rt]=0;//初始化
    if(l==r){
        scanf("%lld",&sum[rt]);
        return ;
    }
    int m=(l+r)>>1;
    build(lson); build(rson);
    PushUp(rt);
}

void update(int L,int R,int c,int l,int r,int rt){
    if(L<=l&&r<=R){
        add[rt]+=c;
        sum[rt]+=(LL)c*(r-l+1);
        return ;
    }
    PushDown(rt,r-l+1);
    int m=(l+r)>>1;
    if(L<=m) update(L,R,c,lson);
    if(mint L,int R,int l,int r,int rt){
    if(L<=l&&r<=R)  return sum[rt];
    PushDown(rt,r-l+1);
    int m=(l+r)>>1;
    LL ret=0;
    if(L<=m) ret+=query(L,R,lson);
    if(R>m) ret+=query(L,R,rson);
    return ret;
}

---

区间覆盖 询问区间和（区间最值同理）

#include
#include
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
const int maxn=200010;
typedef long long LL;

LL cov[maxn<<2];//兼顾lazy标记与具体变化
LL sum[maxn<<2];

void PushUp(int rt){
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}

void PushDown(int rt,int len){
    if(cov[rt]){
        cov[rt<<1]=cov[rt];//下放
        cov[rt<<1|1]=cov[rt];
        sum[rt<<1]=cov[rt]*(len-(len>>1));
        sum[rt<<1|1]=cov[rt]*(len>>1);
        cov[rt]=0;//下放了，清除标记
    }
}

void build(int l,int r,int rt){
    cov[rt]=0;//初始化
    if(l==r){
        scanf("%lld",&sum[rt]);
        return ;
    }
    int m=(l+r)>>1;
    build(lson); build(rson);
    PushUp(rt);
}

void update(int L,int R,int c,int l,int r,int rt){
    if(L<=l&&r<=R){
        cov[rt]=c;
        sum[rt]=(LL)c*(r-l+1);
        return ;
    }
    PushDown(rt,r-l+1);
    int m=(l+r)>>1;
    if(L<=m) update(L,R,c,lson);
    if(mint L,int R,int l,int r,int rt){
    if(L<=l&&r<=R)  return sum[rt];
    PushDown(rt,r-l+1);
    int m=(l+r)>>1;
    LL ret=0;
    if(L<=m) ret+=query(L,R,lson);
    if(R>m) ret+=query(L,R,rson);
    return ret;
}

以上是一些基本操作，在实际问题中会更灵活。另外还有一些操作，如：区间交并补，离散化，区间合并，扫描线（典型的有矩形面积并,周长并）等