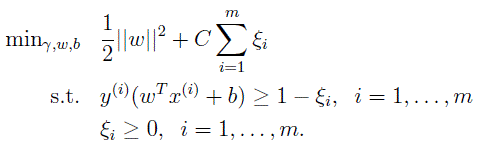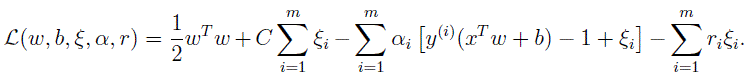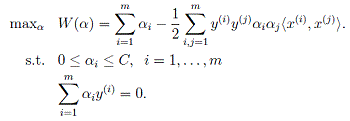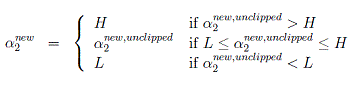SVM-核函数
1.1 SVM非线性可分-核函数
在上一章节中,我们首先假设数据在原始空间上是线性可分的,在这样的前提条件下,我们知道如何求解最大间隔分类器 f(x)=wTx+b=∑mi=1αiy(i)<x(i),x>+b 。但实际上,大多数情况下,数据可能并不是线性可分,你无法在原始数据空间上寻找到这样一条分类超平面,使得数据线性可分。
比如,下面这个例子,很明显蓝色点和红色点应该被归类为两个类别,数据本身又是线性不可分的。但是很容易想到,一个理想的分类界面应该是位于两类数据中心的“圆”而不是直线。(转自:http://blog.csdn.net/v_july_v/article/details/7624837)
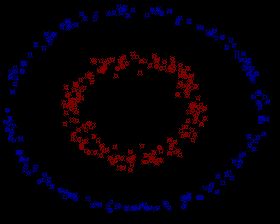
那么尝试将这个假想的分界面用数学表达进行描述。如果以 X,Y 表示二维空间的两个坐标,那么分界面圆的方程可以表示为,
有趣的是,我们可以通过构造另外一个五维度的空间,且其各个坐标值分别为, Z1=X,Z2=X2,Z3=Y,Z4=Y2,Z5=XY ,那么上面的式子可以表达为,
显然在新构造的五维空间下,这个“圆”分界面变成线性的了!那么,可以考虑,如果将所有原始空间的数据通过映射关系: ∅:R2→R5 ,从原始的二维空间映射为五维空间,数据将有可能变成线性可分的。
++++++
如果数据在变换后的高维空间(在上面的例子中是五维度)上是线性可分的,那么我们就可以在这个变换的空间上采用线性SVM计算最优间隔分类器对数据进行分类处理了。SVM在处理线性可分数据时分类器形式为,
假设映射关系 ∅(x) 可以将原始数据映射到特征空间F,且在该空间下,数据是线性可分的,那么在这个空间上的SVM分类器就表示为,
所以,总结上面的非线性数据分类过程应包含两个过程:1.首先使用一个映射关系将数据变换到一个特征空间F上;2.在特征空间上使用线性学习器对数据进行分类。
但是,这会存在另一个问题:我们对二维空间做映射会得到5个维度的特征空间([ x,y,xy,x2,y2 ]),而如果原始空间是3维度,那么转换后的空间将会有19维度(所有一次、二次、三次项),当原始空间数据维度更高时,变换后的特征空间的维度更是无法估计的。当在高维度变换特征空间计算内积时,开销是相当大的。虽然变换到高维空间可以解决低维空间线性不可分的情况,但又引入额外的计算开销。为了解决这个问题,便引入了核函数的概念。
我们还是以原来二维空间的两个数据点进行表示,假设有 x1=(a1,b1)T,x2=(a2,b2)T 按照前面的思路,设映射关系与前面介绍的相同,即 ∅(X,Y)=[X,X2,Y,Y2,XY] 。所以有,
我们再来看一个有趣的式子,
这个式子的基本形式与前一个式子是很类似的。如果我们将变换函数调整为如下形式,
这样再计算 <∅(x1),∅(x2)> ,此时它与 (<x1,x2>+c)2 将会是一样的(具体请自行推导,与上相同,不再赘述)
也就是说,我们得到这样的等式,
两者在计算结果上是等效的,但是计算复杂度却不同! <∅(x1),∅(x2)> 是在高维特征空间上计算内积,而 (<x1,x2>+c)2 却是在低维数据空间上计算内积,而不需要显式得写出在特征空间上的映射数据。 我们把这种可以计算在隐式映射特征空间中内积的函数称为核函数,在我们的例子中,核函数定义为,
那么,好了现在我们可以以较低的计算代价来计算映射特征空间上的内积,再以线性SVM来对数据进行线性分类了。所以,非线性数据SVM分类器可以表示为,
这里列举几个常用的核函数,但实际上,对于低维空间上的线性不可分数据,使用核函数映射到高维特征上,并不会代表数据在高维特征空间上一定线性可分,只能说更接近于线性可分了。根据不同问题,选择的核函数及参数也不尽相同。
多项式核函数
k(x1,x2)=(<x1,x2>+R)d
高斯核函数
线性核
1.2松弛变量处理outliers
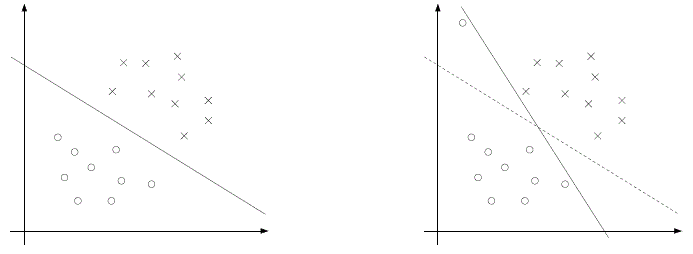
在某些情况下,精确地寻找SVM线性分界面可能并不是我们最想得到的,有些情况因为一些特例的存在使得问题变得不那么理想。比如下面这个例子,左边的图是SVM线性分类结果,右图表示引入一个特例而导致分类界面发生巨大变化,导致间隔(几何间隔)变得更小。
为了使得当前的SVM分类器对这种情况不那么敏感,我们引入一个松弛变量 δi
可以看到,我们允许部分数据的函数间隔小于1,如果说,对于某个数据,其函数间隔为 1−ξ ,那么为了不使松弛变量值过大,我们在目标函数中加入惩罚权重 Cξ ,这样可以保证大多数数据样本的函数间隔不会小于1,但允许部分outliers的存在,这样最终优化的分界面就不会出现右图的情况。
这样,拉格朗日函数将变为,
最终的对偶问题变为,
我们可以看到,与没有加入松弛变量时候唯一不同的地方是 αi 的取值范围不同。相应KKT条件中 αi 和函数间隔对应关系发生如下变化,
1.3 SMO求解对偶问题参数 αi
SMO(sequential minimal optimization)算法,提供了一种高效的方法来解决优化问题中的对偶问题。在介绍SMO是如何求解SVM中优化问题之前,我们首先需要介绍一下坐标上升法,这种方法是SMO中用到的重要理论。
1.3.1坐标上升法
考虑优化问题,
W是关于参数 αi 的优化问题。坐标上升法的主要思想是,每次迭代过程中,只相对于一个变量 αi 进行优化,而其他变量保持不变。而在迭代过程中,对所有变量的优化顺序可以按照 α1,α2,⋯,αm,α1,α2,... 进行。伪代码形式如下,
如果优化参数只有两个 α1,α2 ,那么坐标上升法优化过程可以图示为如下表示,
横坐标表示参数 α1 ,纵坐标表示 α2 。我们可以看出,优化过程迭代交替优化两个参数,每次迭代过程中,保持一个变量值不变,而优化另外一个变量使得目标函数趋近极值点。这里最中心的点为最大值点。
1.3.2 SMO算法
在前面,我们已经提到过对偶问题形式为,
我们可以采用坐标上升法来依次优化每个参数 αi 。假设保持变量 α2,...,αm 不变,优化 α1 使得目标函数 W(α) 最大。但是,通过等式约束条件,我们可以知道,
等式两边同时乘以 y(1) ,我们可以得到,
这是因为 y(1)∈{−1,1} ,所以有 (y(1))2=1 ,所以说,参数 α1 是完全由其他参数和标签数据决定的,在优化过程中 α1 的值并不会发生改变!所以相对于一个变量进行优化是行不通的,那么可以考虑改进为,相对于两个变量进行优化。
假设优化参数为 α1,α2 ,那么有公式,
由于等式右边为一个常量,所以可以重写表示上面等式为,
由于 0≤αi≤C ,所以两个变量的取值是局限在边长为C的矩形框内。参考如下图,
直线表示约束 α1y(1)+α2y(2)=ζ 。为了满足边界约束和等式约束, α2 取值范围为 L≤α2≤H 。根据等式约束 α1y(1)+α2y(2)=ζ ,可以将 α1 表示为 α2 的函数,
那么优化目标函数就可以写成,
如果将参数带入原对偶问题,可以看出这其实是个二次方程式子,也就是说形式上可以表示为 aα22+bα2+c 。那么问题就简单了,求解 α2 就可以通过求导置0的方法求得,然后再根据 α1,α2 的等式约束,可以将参数 α2 求解出来。特别注意的是,在求解 α2 时,需要满足边界约束,当超过边界时, α2 值处理为,
SMO每次选择两个参数,按照上面介绍的算法思路进行优化直至达到收敛条件,SMO优化SVM对偶问题的思路表示为,
总结:经过前两个章节的介绍,我们已经了解到:SVM是寻找线性可分数据的最大间隔的分类器,在数据线性不可分时,可以通过核函数的方法将数据转换为高维空间上进行计算,这个过程可以使得原始线性不可分的数据在高维空间上更接近于线性可分。核函数不仅实现了这种低维到高维空间的变换,同时也减少了在高维空间计算内积的高复杂性,而是将问题锁定在低维空间上的内积运算,大大降低了运算复杂度。但是选择何种核函数,确定何种参数,还需要根据具体问题具体分析。
如有问题,欢迎指正~