NOIP模拟赛2019.9.14题解
T1 刺客信条(AC)
100pts
并查集+二分答案
要使最小距离最大化。对于每次二分的最小距离d,两两计算所有教徒的距离,若这个距离小于d*2,那么这两个教徒连一条边(加入到同一个并查集中),代表一个障碍,即不能从这两者之间经过。并把和边界的距离小于d的教徒与边界连边。当所有的障碍全部连起来能够挡住从(0,0)到(x,y)的路,则此情况不成立。
挡住路有四种情况:上下边界在同一个并查集;左右边界在同一个并查集;
左下边界在同一个并查集;右上边界在同一个并查集。
画个图就一目了然了。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=2005;
int fx,fy,n;
double a[N],b[N],f[1000005];
int read(){
int sum=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){sum=(sum<<3)+(sum<<1)+ch-'0';ch=getchar();}
return sum*f;
}
void print(int x)
{
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10+'0');
}
int find(int x)
{
if(x==f[x])return x;
return f[x]=find(f[x]);
}
void join(int x,int y)
{
x=find(x);y=find(y);
f[x]=y;
}
bool check(double d){
for(int i=1;i<=n+4;i++)
f[i]=i;
for(int i=1;i<=n;i++)
{
if(a[i]<d)join(i,n+1);
if(a[i]+d>fx)join(i,n+2);
if(b[i]<d)join(i,n+3);
if(b[i]+d>fy)join(i,n+4);
}
double q=4*d*d;
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
{
double len=(a[i]-a[j])*(a[i]-a[j])+(b[i]-b[j])*(b[i]-b[j]);
if(len<q)join(i,j);
}
if(find(n+1)==find(n+2))return false;
if(find(n+1)==find(n+3))return false;
if(find(n+2)==find(n+4))return false;
if(find(n+3)==find(n+4))return false;
return true;
}
int main(){
// freopen("AC.in","r",stdin);
// freopen("AC.out","w",stdout);
fx=read();fy=read();
n=read();
for(int i=1;i<=n;i++)
{a[i]=read();b[i]=read();}
double l=0,r=1000005,mid;
while(l+0.001<r)
{
mid=1.0*(l+r)/2;
if(check(mid))l=mid;
else r=mid;
}
printf("%.2lf",l);
return 0;
}
T2 黑暗之魂(darksoul)
100pts
发现这是一个环套树。
若有自环和重边,去除后就变成了一棵树,直接树形DP就可以了。
否则的话先用tarjan求强连通分量找出这个环,然后把问题分解成在环上和树上处理(树形DP)两部分。
树形DP:从下往上递归求当前子树的最长链和次长链将其组成一条链更新答案。
处理环:用单调队列优化,发现求环上任意两点连接链的长度就是:
d e p [ i d [ i ] ] + s u m [ i − 1 ] + d e p [ i d [ h [ l ] ] ] − s u m [ h [ l ] − 1 ] ; dep[id[i]]+sum[i-1]+dep[id[h[l]]]-sum[h[l]-1]; dep[id[i]]+sum[i−1]+dep[id[h[l]]]−sum[h[l]−1];(这个长度一定小于等于环长的一半)
那么就保证队列中 d e p [ i d [ h [ i ] ] ] − s u m [ h [ i ] − 1 ] dep[id[h[i]]]-sum[h[i]-1] dep[id[h[i]]]−sum[h[i]−1]单调不增就行了,否则队尾的答案一定比前面的更优,要弹出前面的。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=2000005;
typedef long ll;
int n,tot=0,head[N],v[N],cnt,t,big,cs,flag,idx;
int huan[N],dfn[N],low[N],id[N],w[N],h[N],sta[N],siz[N],has[N];
ll dep[N],ans,sum[N];
struct node{
int x,y,z;
}a[N];
struct edge{
int ver,to,w;
}e[N];
void add(int x,int y,int z)
{
e[++tot].ver=y;
e[tot].to=head[x];
e[tot].w=z;
head[x]=tot;
}
bool comp(node a,node b){
if(a.x==b.x)
{
if(a.y==b.y)return a.z<b.z;
return a.y<b.y;
}
return a.x<b.x;
}
int read(){
int sum=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){sum=(sum<<3)+(sum<<1)+ch-'0';ch=getchar();}
return sum*f;
}
void print(ll x)
{
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar(x%10+'0');
}
void dp(int x,int fa)
{
ll max1=0,max2=0;
for(int i=head[x];i;i=e[i].to)
{
int y=e[i].ver;
if(y==fa||(!flag&&huan[y]==big))continue;
dp(y,x);
ll len=dep[y]+e[i].w;
if(len>max1){max2=max1;max1=len;}
else if(len>max2)max2=len;
}
ans=max(ans,max1+max2);
dep[x]=max1;
}
void tarjan(int x,int fa)
{
dfn[x]=low[x]=++idx;
v[x]=1;
sta[++t]=x;
for(int i=head[x];i;i=e[i].to)
{
int y=e[i].ver;
if(y==fa)continue;
if(!dfn[y]){
tarjan(y,x);
low[x]=min(low[x],low[y]);
}
else if(v[y])
low[x]=min(low[x],dfn[y]);
}
if(low[x]==dfn[x]){
int now=sta[t--];
cs++;
while(now!=x)
{
huan[now]=cs;
siz[cs]++;
v[now]=0;
now=sta[t--];
}
huan[now]=cs;
v[now]=0;
siz[cs]++;
if(siz[big]<siz[cs])big=cs;
}
}
void dfs(int x,int fa){
id[++cnt]=x;
has[x]=1;
dp(x,x);
for(int i=head[x];i;i=e[i].to)
{
int y=e[i].ver;
if(y==fa||huan[y]!=big)continue;
w[cnt]=e[i].w;
if(!has[y])dfs(y,x);
}
}
int main(){
// freopen("darksoul.in","r",stdin);
// freopen("darksoul.out","w",stdout);
n=read();
int x,y;
for(int i=1;i<=n;i++)
{
x=read();y=read();a[i].z=read();
if(x>y)swap(x,y);
a[i].x=x;a[i].y=y;
}
sort(a+1,a+n+1,comp);
for(int i=1;i<=n;i++)
{
if(a[i].x==a[i-1].x&&a[i].y==a[i-1].y)flag=1;
else if(a[i].x==a[i].y)flag=1;
else add(a[i].x,a[i].y,a[i].z),add(a[i].y,a[i].x,a[i].z);
}
if(flag){
dp(1,1);
print(ans+1);
return 0;
}
tarjan(1,1);
for(int i=1;i<=n;i++)
{
if(huan[i]==big){dfs(i,i);break;}
}
for(int i=1;i<=cnt;i++)
id[i+cnt]=id[i],w[i+cnt]=w[i];
for(int i=1;i<=cnt*2;i++)
sum[i]=sum[i-1]+w[i];
int l,r;
l=r=1;h[1]=1;
for(int i=2;i<=tot*2;i++)
{
while(l<=r&&sum[i-1]-sum[h[l]-1]>sum[cnt]/2)l++;
if(l<=r)ans=max(ans,dep[id[i]]+sum[i-1]+dep[id[h[l]]]-sum[h[l]-1]);
while(l<=r&&dep[id[h[r]]]-sum[h[r]-1]<=dep[id[i]]-sum[i-1])r--;
h[++r]=i;
}
print(ans+1);
return 0;
}
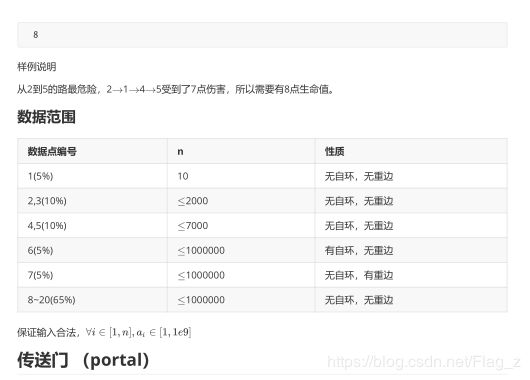
T3 传送门 (portal)
100pts
树形DP
f [ x ] [ 0 ] f[x][0] f[x][0]表示以x为根的子树没有用到传送门
f [ x ] [ 1 ] f[x][1] f[x][1]表示以x为根的子树没有用到传送门
状态转移方程:
f [ x ] [ 0 ] + = f [ y ] [ 0 ] + e [ i ] . w ∗ 2 f[x][0]+=f[y][0]+e[i].w*2 f[x][0]+=f[y][0]+e[i].w∗2 (y为x的儿子,e[i].w为x与y的边,显然要来回共走2次)
f [ x ] [ 1 ] + = m i n ( f [ y ] [ 1 ] + e [ i ] . w ∗ 2 , f [ y ] [ 0 ] − d e p [ y ] + e [ i ] . w ) f[x][1]+=min(f[y][1]+e[i].w*2,f[y][0]-dep[y]+e[i].w) f[x][1]+=min(f[y][1]+e[i].w∗2,f[y][0]−dep[y]+e[i].w)
两种情况:1.x节点用传送门;2. x的子树中的节点用传送门。取更小的值。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
typedef long ll;
int n,x,y,ans,tot,head[N],fa[N];
ll z,f[N][2],dep[N];
struct edge{
int to,v;
ll w;
}e[N*2];
ll read(){
ll sum=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){sum=(sum<<3)+(sum<<1)+ch-'0';ch=getchar();}
return sum*f;
}
void add(int x,int y,ll z)
{
e[++tot].v=y;
e[tot].to=head[x];
e[tot].w=z;
head[x]=tot;
}
void dp(int x)
{
for(int i=head[x];i;i=e[i].to)
{
int y=e[i].v;
if(y==fa[x])continue;
fa[y]=x;
dp(y);
dep[x]=max(dep[x],dep[y]+e[i].w);
f[x][0]+=f[y][0]+e[i].w*2;
f[x][1]+=min(f[y][1]+e[i].w*2,f[y][0]-dep[y]+e[i].w);
}
}
void print(ll x)
{
if(x<0)x=-x,putchar('-');
if(x>9)print(x/10);
putchar(x%10+'0');
}
int main(){
// freopen("portal.in","r",stdin);
// freopen("portal.out","w",stdout);
n=read();
for(int i=1;i<n;i++)
{
x=read();y=read();z=read();
add(x,y,z);
add(y,x,z);
}
fa[1]=0;
dp(1);
print(min(f[1][0],f[1][1]));
return 0;
}