剑指Offer66题之每日6题 - 第五天
原题链接:
- 第一题:复杂链表的复制;
- 第二题:二叉搜索树与双向链表;
- 第三题:字符串的排列;
- 第四题:数组中出现次数超过一半的数字;
- 第五题:最小的K个数;
- 第六题:连续子数组的最大和;
第一题:复杂链表的复制
题目:
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针指向任意一个节点),返回结果为复制后复杂链表的
head。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)
解析:
假如这题没有随机指针,很好搞,问题是有了随机指针,如何在新建结点的时候令随机指针指向正确的位置?可以用一个
map来映射原结点和对应的新结点,刚开始的时候不要管随机指针,按照没有随机指针来做,把map填上;这样搞完后,再遍历一遍新链表,利用map中的映射来确定随机指针,下面分别给出递归做法和非递归做法。
/*
struct RandomListNode {
int label;
struct RandomListNode *next, *random;
RandomListNode(int x) :
label(x), next(NULL), random(NULL) {
}
};
*/
class Solution {
public:
RandomListNode* Clone(RandomListNode* pHead)
{
map/*
struct RandomListNode {
int label;
struct RandomListNode *next, *random;
RandomListNode(int x) :
label(x), next(NULL), random(NULL) {
}
};
*/
class Solution {
public:
RandomListNode* Clone(RandomListNode* pHead)
{
if (pHead == nullptr)
return nullptr;
map如果不用
map这个数据结构该怎么搞呢?还是要解决原结点和对应新结点之间的映射关系,如何搞?看下面的步骤:
- 每新建一个结点就把该结点插入到原链表对应的原结点后;
- 上一步全部完成后,遍历原链表(2倍长度了),由于原结点和新结点之间是相邻的,因此只要
p->next就可以通过原结点找到对应的新结点,这样就解决了这个映射关系,这一步确定随机指针;- 最后一步就是把加长后的链表拆分出来,这样即保证创建了新链表,也保证了原链表没有被破坏。
/*
struct RandomListNode {
int label;
struct RandomListNode *next, *random;
RandomListNode(int x) :
label(x), next(NULL), random(NULL) {
}
};
*/
class Solution {
public:
RandomListNode* Clone(RandomListNode* pHead)
{
if (pHead == nullptr)
return nullptr;
RandomListNode *p = pHead, *ret = pHead;
for (; p != nullptr; p = p->next->next) {
RandomListNode *now = new RandomListNode(p->label);
now->next = p->next;
p->next = now;
}
for (p = pHead; p != nullptr; p = p->next->next)
if (p->random != nullptr)
p->next->random = p->random->next;
for (p = pHead, ret = p->next; p->next != nullptr;
pHead = p->next, p->next = p->next->next, p = pHead);
return ret;
}
};第二题:二叉搜索树与双向链表
题目:
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
解析:
还是分递归做法和非递归做法。先说递归做法。
这里要引入一个
pre指针,它表示上次刚遍历过的结点的地址;在递归的过程中要返回最小的那个结点,由于是中序遍历,那么最小的那个结点一定在左子树(如果有左子树);我们只需要修改当前节点的左指针了,pre指向结点的右指针就行了,具体修改如下:
root->left = pre;pre->right = root。上面两步操作都建立在
root和pre不为空的情况下,具体的边界可以自己推敲下,或者看我的代码,候捷大师说过:“源码之前,了无秘密” ,我们都应该多去源码中寻找细节,发现秘密。扯远了,这里还需要注意一点,按理说还要修改root和下一个结点之间的关系,但是其实这是没有必要的,当遍历到下一个结点时,下一个结点就成为了当前结点,root就成为了pre,这个关系会在这里修改的,所以不需要多此一举修改root和下一个结点之间的关系。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
TreeNode *pre = nullptr;
return convert(pRootOfTree, &pre);
}
TreeNode* convert(TreeNode* pRootOfTree, TreeNode **pre)
{
if (pRootOfTree == nullptr)
return nullptr;
auto ret = convert(pRootOfTree->left, pre);
if (ret == nullptr)
ret = pRootOfTree;
if (*pre != nullptr)
(*pre)->right = pRootOfTree;
pRootOfTree->left = *pre;
convert(pRootOfTree->right, (*pre = pRootOfTree, pre));
return ret;
}
};非递归做法还是利用二叉排序树中序遍历的非递归写法,看下这篇博客;不过还是需要引入
pre指针,非递归的代码其实就是我在中序遍历的非递归写法上加了点东西就搞定了,思想还是和递归做法的一样。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
if (pRootOfTree == nullptr)
return pRootOfTree;
typedef TreeNode *pNode;
stack第三题:字符串的排列
题目:
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串
abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。输入一个字符串,长度不超过
9(可能有字符重复),字符只包括大小写字母。
解析:
这题一看,首先必然是利用库函数
next_permutation来做,然后set去重。关于
next_permutation的用法和源码可以看下我早年写的一篇博客,点这儿, 刚开始写博客就写了这个函数,那个时候没有过多的解释源码,这个源码待会我也会用到,之后会对 STL 做系统的源码阅读,到时候也会以博客的形式呈现出来,这里就不多做解释了。
class Solution {
public:
vector<string> Permutation(string str) {
vector<string> ret;
if (str.size() == 0)
return ret;
set<string> se;
sort(str.begin(), str.end());
do {
se.insert(str);
} while(next_permutation(str.begin(), str.end()));
for (auto it = se.begin(); it != se.end(); ret.push_back(*it++));
return ret;
}
};全排列算法也是我 ACM 生涯中遇到第一个算法,当时是求解
123456的全排列,我用了dfs,开一个bool类型的used数组来存储1到6之间的数字在之前是否出现过;然后从前往后依次去填充。这样可以保证最后结果一定是字典序的。但是这里字母可能有重复,没关系啊,把used的类型改成int类型就行了,里面存储的是还有几个这样的字母可以用来填充。我一般也喜欢用这个算法来全排列。
class Solution {
public:
vector<string> Permutation(string str) {
vector<string> ret;
if (str.size() == 0)
return ret;
vector<int> cnt(26 * 2, 0);
for (int i = 0; i < (int)str.size(); ++cnt[mapToIndex(str[i++])]);
dfs(cnt, ret, "", str.size());
return ret;
}
int mapToIndex(char c)
{
return islower(c) ? c - 'a' : c - 'A' + 26;
}
void dfs(vector<int> &cnt, vector<string> &ret, string str, int n)
{
if (str.size() == n) {
ret.push_back(str);
return ;
}
for (int i = 0; i < 26 * 2; i++)
if (cnt[i]) {
--cnt[i];
dfs(cnt, ret, str + (char)(i < 26 ? 'a' + i : 'A' + i - 26), n);
++cnt[i];
}
}
};这题也有非递归的写法,其实就是我上面提到的
next_permutation的实现,模版库函数中的实现就是非递归的,只需要修改下源码就行了。
class Solution {
public:
vector<string> Permutation(string str) {
typedef string::iterator _BI;
vector<string> ret;
_BI _F = str.begin(), _L = str.end();
_BI _I = _L;
if (_F == _L)
return ret;
if (_F == --_I) {
ret.push_back(str);
return ret;
}
ret.push_back((sort(_F, _L), str));
for (bool f = false; !f; _I = _L, --_I) {
for (; ; ) {
_BI _Ip = _I;
if (*--_I < *_Ip) {
_BI _J = _L;
for (; !(*_I < *--_J); );
iter_swap(_I, _J);
reverse(_Ip, _L);
ret.push_back(str);
break;
}
if (_I == _F) {
reverse(_F, _L);
f = true;
break;
}
}
}
return ret;
}
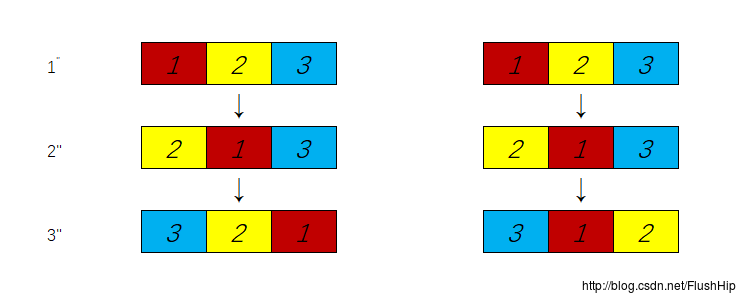
};剩下的就是全排列的教科书式算法了。这个算法百度都有的,改一下交换条件,如果两数相等就不交换,因为交换了还是一样的结果,这样就重复了。不过要注意的点是如果传递给函数的数组是原数组,而不是数组的复制品,那么是得不到字典序的,虽然全排列的结果是对的;如果采用的是传递数组的复制品,那么也不要复位的
swap,要了也得不到字典序,看下图,解释了原因:假如你复位了,那么交换过程中序列就是左边所示,可以看到, 3′′ 中的
21并不是字典序中最小的,故得不到字典序;没有复位,交换过程中的序列就如右边所示,可以看到,后两位一直都是字典序中最小的,这样才能得到整体字典序。
class Solution {
public:
vector<string> Permutation(string str) {
vector<string> ret;
if (str.size() == 0)
return ret;
sort(str.begin(), str.end());
permutation(str, ret, 0);
return ret;
}
void permutation(string str, vector<string> &ret, unsigned int start)
{
if (start == str.size()) {
ret.push_back(str);
return ;
}
for (unsigned int i = start; i < str.size(); i++) {
if (i == start || str[i] != str[start]) {
swap(str[i], str[start]);
permutation(str, ret, start + 1);
// swap(str[i], str[start]);
}
}
}
};第四题:数组中出现次数超过一半的数字
题目:
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为
9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
解析:
这题我在好未来2017秋招笔试真题一 - 解析的第15题讲过,不会的可以去看一下。
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int> numbers) {
int cnt = 0, flag = 0, i;
for (i = 0; i < (int)numbers.size(); i++)
!cnt ? (flag = numbers[i], cnt = 1) : flag == numbers[i] ? ++cnt : --cnt;
for (cnt = 0, i = 0; i < (int)numbers.size(); cnt += (numbers[i++] == flag));
return cnt > (int)numbers.size() / 2 ? flag : 0;
}
};现在把这个问题改一下,求出数组中出现次数大于 1k 的所有数。
首先,我们要确定一点,符合条件的数的个数一定小于
k,这个你要承认。 原始问题中,是设一个哨兵,那么这里我们就设k - 1个哨兵,遍历数组,当前值与这k - 1个哨兵都不相等时,就使其哨兵对应的数量都减一,最后判断下这k - 1个哨兵到底是不是满足条件就行了,如何保存这k - 1个哨兵和其对应的数量呢?用map。我编写了
MoreThanK_Num_Solution这个函数来求解这个扩展问题,那么k = 2就是这个扩展问题的一个个例,自然原始问题是可以调用这个函数的,下面的代码在牛客网通过。
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int> numbers) {
auto ret = MoreThanK_Num_Solution(numbers, 2);
return ret.size() == 0 ? 0 : ret[0];
}
vector<int> MoreThanK_Num_Solution(vector<int> numbers, int k) {
map<int, int> mp;
for (int i = 0; i < (int)numbers.size(); i++) {
if (mp.find(numbers[i]) != mp.end())
++mp[numbers[i]];
else if (mp.size() < k - 1)
mp[numbers[i]] = 1;
else {
for (auto it = mp.begin(); it != mp.end(); it->second--, ++it);
for (auto it = mp.begin(); it != mp.end(); !it->second ? it = mp.erase(it) : ++it);
}
}
vector<int> ret;
for (auto it = mp.begin(); it != mp.end(); ++it) {
int cnt = 0;
for (int i = 0; i < (int)numbers.size(); i++)
cnt += (numbers[i] == it->first);
if (cnt > (int)numbers.size() / k)
ret.push_back(it->first);
}
return ret;
}
};第五题:最小的K个数
题目:
输入
n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4。
解析:
最简单的做法就是调用
sort函数,然后返回前K个元素就可以了。
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
vector<int> ret;
if (input.size() < k)
return ret;
sort(input.begin(), input.end());
for (int i = 0; i < k; ret.push_back(input[i++]));
return ret;
}
};既然排序可以做,那么用
multiset(不能用set,set会去重)和priority_queue也是可以做的,一个基于红黑树实现,一个基于堆实现。
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
vector<int> ret;
if (input.size() < k)
return ret;
multiset<int> mse;
for (auto it = input.begin(); it != input.end(); mse.insert(*it++));
for (auto it = mse.begin(); k--; ret.push_back(*it++));
return ret;
}
};
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
vector<int> ret;
if (input.size() < k)
return ret;
priority_queue<int, vector<int>, greater<int> > que;
for (auto it = input.begin(); it != input.end(); que.push(*it++));
for (; k--; ret.push_back(que.top()), que.pop());
return ret;
}
};这题还可以改进一下,利用快排的原理来做,其实就是把快排的代码稍微修改一下,快排的代码可以看看这儿。
快排的思想是选定一个基准划分数组,使得基准左边的元素均小于基准,右边的元素均大于基准,递归下去就行了;
那么是否有必要把整个数组都划分完呢,其实没必要的,具体划分细节如下:
- 如果左边元素的个数小于等于
k - 1,那么划分左边的全部元素,右边的元素划分前k - low + l - 1个就行了;- 如果左边的元素个数大于
k - 1,那么划分左边前k - 1个元素就行了,右边的元素不用划分。
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
vector<int> ret;
if (input.size() < k)
return ret;
partion(input, k, 0, input.size() - 1);
for (int i = 0; i < k; ret.push_back(input[i++]));
return ret;
}
void partion(vector<int> &input, int k, int l, int r)
{
if (l >= r || k <= 0)
return ;
int tmp = input[l], low = l, high = r;
while (low < high) {
for (; low < high && tmp < input[high]; high--);
if (low < high)
input[low++] = input[high];
for (; low < high && tmp > input[low]; low++);
if (low < high)
input[high--] = input[low];
}
input[low] = tmp;
partion(input, min(low - l, k - 1), l, low);
partion(input, k - low + l - 1, low + 1, r);
}
};第六题:连续子数组的最大和
题目:
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?
例如:
{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。你会不会被他忽悠住?(子向量的长度至少是1)。
解析:
这题真的是经典,已经不能再经典了,我逐一给出复杂度由高到底的各种算法,并且给出这个问题的扩展问题求出子数组的左右端点和连续子数组最大积的解法。
暴力法,先预处理出前缀和,然后枚举子数组的长度和起点,维护一个最大值就行了。
时间复杂度: O(n2) ;
空间复杂度: O(n) 。
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
vector<int> sum(array);
int ret = -0x3f3f3f3f;
for (int i = 1; i < (int)array.size(); sum[i] = sum[i - 1] + array[i], ++i);
for (int len = 1; len <= (int)array.size(); ++len)
for (int i = 0; i + len - 1 < (int)array.size(); ++i)
ret = max(ret, sum[i + len - 1] - (i ? sum[i - 1] : 0));
return ret;
}
};既然暴力法时间复杂度为 O(n2) ,那么有一句话叫 只会暴力的O(n2),会二分的O(nlogn),会动态规划的O(n),会数学的就O(1) 。那么这个题我们是不是可以也二分搞一下然后优化到 O(nlogn) 呢?答案是可以的。
考虑一下这个最大和的子数组会在数组中的什么位置呢?答案无非就是下面三种情况:
- 位置在数组中点的左边;
- 位置在数组中点的右边;
- 位置跨过中点,中点的两边都有。
情况一、二都可以递归解决,问题是情况三怎么搞?如果是情况三,那么只需要开两个循环分别从中点的左边和右边维护下靠近中点的连续数组的最大和就行了。
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
return dfs(array, 0, array.size());
}
int dfs(vector<int> &array, int l, int r)
{
if (r - l == 1)
return array[l];
int mid = (r + l) / 2, ll = dfs(array, l, mid), rr = dfs(array, mid, r);
int left = -0x3f3f3f3f, right = left, sum = 0, i;
for (i = mid - 1; i >= l; left = max(left, sum += array[i--]));
for (i = mid, sum = 0; i < r; right = max(right, sum += array[i++]));
return max(max(ll, rr), left + right);
}
};上面的这个代码还能不能优化呢,可以的,在
dfs中,这两个for循环其实可以预处理出来,这样,dfs的时间复杂度就为 O(logn) ,但是预处理的时间为 O(n) ,所以整体的复杂度为 O(n) 。
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
vector<int> sum_l(array), sum_r(array);
for (int i = 1; i < (int)array.size(); sum_l[i] = max(array[i], sum_l[i - 1] + array[i]), i++);
for (int i = (int)array.size() - 2; i >= 0; sum_r[i] = max(array[i], sum_r[i + 1] + array[i]), i--);
return dfs(array, 0, array.size(), sum_l, sum_r);
}
int dfs(vector<int> &array, int l, int r, vector<int> &sum_l, vector<int> &sum_r)
{
if (r - l == 1)
return array[l];
int mid = (r + l) / 2, ll = dfs(array, l, mid, sum_l, sum_r), rr = dfs(array, mid, r, sum_l, sum_r);
int left = -0x3f3f3f3f, right = left, sum = 0, i;
return max(max(ll, rr), sum_l[mid - 1] + sum_r[mid]);
}
};不知道你有没有注意到我刚才说的一句话: 只会暴力的O(n2),会二分的O(nlogn),会动态规划的O(n),会数学的就O(1) ,上面这个优化代码时间复杂度是 O(n) 的啊,不是说二分只有 O(nlogn) 吗,优化之后怎么和动态规划的时间复杂度一样了啊?其实上面的预处理就是简单的线性动态规划,也就是,我们完全可以在预处理
sum_l时直接维护一个最大值,这个最大值就是答案,为什么呢,我们在求sum_l时枚举了子数组的右端点,左端点不知道,不过没关系啊,只要这个最大值能从前一个最大值推过来,那还管什么左端点啊,这样下来我们就枚举了子数组的所有情况(也不能完全说所有状态吧,我们只是枚举了确定的右端点的最大和的子数组,不是最大和的子数组对于我们来说没用,因此不用管)。这样,这个最大值就是合法的。这样可以得出结论,后面的
dfs完全没有必要了,这也是为什么优化后的代码时间复杂度为 O(n) 的原因,故分治法根本就没谁用。 下面给出动态规划的代码。时间复杂度: O(n) ;
空间复杂度: O(n) 。
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
vector<int> sum_l(array);
int ret = -0x3f3f3f3f;
for (int i = 1; i < (int)array.size(); sum_l[i] = max(array[i], sum_l[i - 1] + array[i]), i++);
for (int i = 0; i < (int)sum_l.size(); ret = max(ret, sum_l[i++]));
return ret;
}
};关于这个动态的规划的代码还有一种的写法,空间复杂度: O(1) 。
思想是这样的,其实和动态规划的思想一样,只不过我在动态规划代码中没这么写而已,看这行代码
sum_l[i] = max(array[i], sum_l[i - 1] + array[i]),你细心点可以发现,这里根本需要max函数,影响这两个数大小的关键点是sum_l[i - 1]是否大于0,所以可以这样写sum_l[i] = sum[i - 1] > 0 ? sum[i - 1] + array[i] : array[i],什么意思呢?就是说如果前面的连续和小于0,那么对后面的连续和会有反作用,一定会使连续和变小,故要砍掉。看代码。
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
int ret = array[0];
for (int sum = 0, i = 0; i < (int)array.size(); ++i)
ret = max(ret, sum = (sum > 0 ? sum + array[i] : array[i]));
return ret;
}
};现在来说这题的扩展问题一之求出子数组的左右端点,这题在HDU上有原题HDU1003,我直接贴出代码吧,求端点真的很简单。下面的代码依次是动态规划法和线性求解法。
#include #include 扩展问题二之连续子数组最大积,这在我之前的博客中已经讨论过了,大家可以参阅下,点这儿。