多元高斯分布
多元高斯分布
1.协方差矩阵
协方差衡量的是变量X与Y之间是否存在线性关系,cov(X,Y)>0说明X与Y的变化趋势是一致的,X增长的时候Y也随着增长。如果X,Y互相独立的话,cov(X,Y)=0.
cov(X,X)=D(X),变量X与自身的协方差就是方差,cov(X,Y)=cov(Y,X),cov(X,Y)=E[(X-E(X))(Y-E(Y))].
注意,上述变量X,Y都是一维变量,因此他们的协方差是一个数,如果X∈![]() ,Y∈
,Y∈![]() ,那么X,Y的协方差矩阵就是一个n*n的矩阵,也就是协方差矩阵,关于协方差矩阵的介绍可以查看协方差矩阵.
,那么X,Y的协方差矩阵就是一个n*n的矩阵,也就是协方差矩阵,关于协方差矩阵的介绍可以查看协方差矩阵.
一定要记住,期望,方差,协方差这些统计量都是针对的一维随机变量来说的,传统的高斯分布也是针对一维随机变量,通过平均数u和方差![]()
![]() σ^2来定义,当扩展到多维数据的时候就要使用多元高斯分布来进行刻画,此时参数就变为了u和Σ(协方差矩阵),u是一个n维向量,Σ是n*n的矩阵。
σ^2来定义,当扩展到多维数据的时候就要使用多元高斯分布来进行刻画,此时参数就变为了u和Σ(协方差矩阵),u是一个n维向量,Σ是n*n的矩阵。
协方差矩阵的定义上面已经说了,http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/介绍了一下Σ的意义,Σ实际上是一个线性变换函数,可以使用Σ来对原始数据D进行相应的变换,其中一些比较有用的话如下,具体请查看博客:
1.the largest eigenvector of the covariance matrix always points into the direction of the largest variance of the data, and the magnitude of this vector equals the corresponding eigenvalue. The second largest eigenvector is always orthogonal to the largest eigenvector, and points into the direction of the second largest spread of the data.
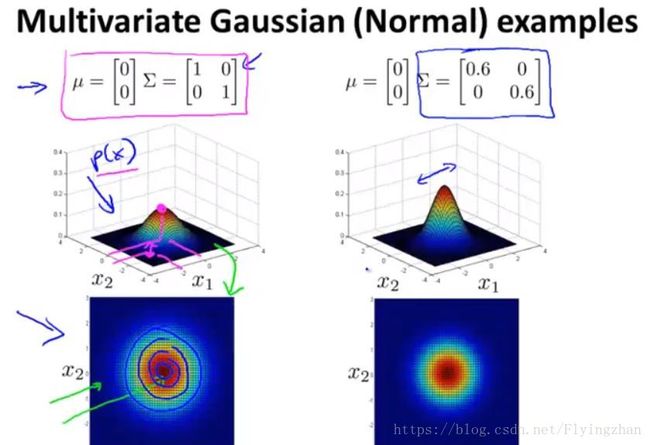
通过PCA我们知道,最大特征值对应的特征向量具有最大的方差,我感觉这里说的比较好的一点就是方差越大数据的spread就越大,这一点可以通过下图来看出:
上图截取自andrew ng在coursera上的机器学习课程的multivariate gaussian distribution一节中,由于Σ对角线上的元素的值就是变量的方差,可以看出,当x2的方差等于1的时候大于0.6的时候。
2.we showed that the covariance matrix of observed data is directly related to a linear transformation of white, uncorrelated data. This linear transformation is completely defined by the eigenvectors and eigenvalues of the data. While the eigenvectors represent the rotation matrix, the eigenvalues correspond to the square of the scaling factor in each dimension.
2.多元高斯分布
多元高斯分布的详细介绍请查看博客https://www.cnblogs.com/jermmyhsu/p/8251013.html,这里我想说的主要是下面一点。如果我们需要估计一些数据分布接近于高斯分布的变量时,存在两种解法。一种就是把特征的第一维当做一个一维的变量,然后使用u1以及σ1来衡量他的分布,同样,对于第二维使用u2以及σ2来衡量,然后将得到的obj=p(x1; u1, σ1)*p(x2; u2, σ2)*...*p(xn; un, σn)来当做最终的目标函数进行优化,使用最大似然估计来得到较好的分布估计。但是我们也可以使用多元高斯分布来代替,此时p(x)=p(x;u,Σ).
通过求偏导我们可以得到u,Σ的最优解。
多元高斯分布和上面所说的将第一维当做一个一维的变量,然后使用u1以及σ1来衡量他的分布,同样,对于第二维使用u2以及σ2来衡量,然后将得到的obj=p(x1; u1, σ1)*p(x2; u2, σ2)*...*p(xn; un, σn)的模型有着联系,后者是多元高斯分布的一种特例,当n维变量X的每一维都相互独立,也就是说多元高斯分布对应的Σ是一个对角矩阵,除了主对角线上的数外,其余数都为0,此时多元高斯分布可以写成上述形式,注意,模型obj没有要求每一维是相互独立的。
原始的模型计算复杂度比较小,多元高斯模型计算复杂度较大,但是效果更好。通过人为构造一些捕捉不同维度之间关系的维度能够得到更好的效果,而当训练样本数远大于数据维度的时候使用多元高斯分布能够取得很好的效果。
3:马氏距离(Mahalanobis distance)
下面是马氏距离的一些基本概念,可以看到,马氏距离的表达式和多元高斯分布exp()里面的表达式一致,至于原因是为什么我不太清楚,这一点需要再查一下,如果有知道的请评论一下,谢谢。
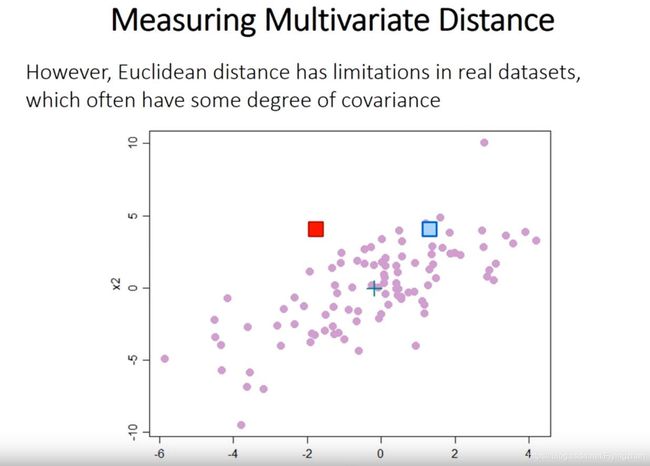
对于欧式举例来说,下面的红蓝两个点和中心点(叉)有相同的距离,但是由于变量x1,x2是具有相关性的,因此可以看出数据分布实际上是条形的,因此这个时候红色的点接近于边缘,甚至可以视为离群点(outlier),因此在这种情况下,欧式距离是不适用的。 通过一些变化将原始的数据分布进行坐标变换如PCA,变化之后的数据就可以使用欧氏距离进行距离度量。
除此之外,对于一些具有不同尺度的数据,直接使用欧式距离计算是不合适的,如下面的A,B,C三组数据:
如果特征x和y具有不同的尺度,那么直接计算欧几里得距离的话,可以很直观的看出,距离主要取决于数据量较大的一组,因此结果是不准确的,所以很多数据都会做预处理,比如说z-score,min-max之类的变换尺度的方法。
马氏距离也可以看成先将数据进行尺度变换,类似于(x-u)/σ,然后在进行距离计算。
下面这篇论文从公式介绍了该过程:
https://www.cnblogs.com/DPL-Doreen/p/8183909.html
可以看出,马氏距离实际上就是将原始分布做PCA之后再次进行欧氏距离度量的方法。
参考文献:
http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/
https://www.youtube.com/watch?v=spNpfmWZBmg
https://www.youtube.com/watch?v=3IdvoI8O9hU
https://www.cnblogs.com/DPL-Doreen/p/8183909.html