量子纠缠态

波尔和爱因斯坦的第三次争论，本来应该发生在 1933 年的第七届索尔维会议上。但 是，爱因斯坦未能出席这次会议，他被纳粹赶出了欧洲，刚刚风尘仆仆地到达美国，被应聘 为普林斯顿高等研究院教授。德布罗依和薛定谔出席了会议，但薛定谔见双龙无首不想发 言，德布罗依呢，据说是个法国贵族出身的花花公子，曾经用一页纸的论文打发结束了晃荡 了五年的博士生涯，哪有精神去与这些人辩论啊。这令波尔大大松了一口气，会议上哥本哈 根派唱独角戏，看起来量子论已经根基牢靠，论战似乎尘埃落定。 

然而，爱因斯坦毕竟是个伟人，不是那么容易服输的。况且，那是上帝给他的使命：为 物理学指路！无论是开创还是质疑，无论是披荆斩棘地朝前带领大军，还是回头转身，来一 场唇枪舌战，其结果都是顺应天意：使物理这条猛兽不停地冲出困境，向前迈进。尽管他当 时因战争而流离失所，尽管他的妻子身染重病，到了知天命年龄的爱因斯坦，始终未忘记他 的这个神圣的‘天命’。 

笔者的老师和论文委员会成员之一的约翰·惠勒（John Archibald Wheeler），曾经在 一次聚会上，对笔者说过一段爱因斯坦的故事：1948 年，普林斯顿的费曼在惠勒的指导下， 完成了他的博士论文，他以惠勒早期的一个想法为基础，开创了用路径积分来表述量子力 学的方法。当年，惠勒曾经将费曼的论文交给爱因斯坦看，并对爱因斯坦说：“这个工作不 错，对吧？”又问爱因斯坦：“现在，你该相信量子论的正确性了吧！”爱因斯坦沉思了好一 会儿，脸色有些灰暗，怏怏不快地说：“也许我有些什么地方弄错了。不过，我仍旧不相信 老头子（上帝）会掷骰子！” 

再回到波爱第 3 次论战：当年的爱因斯坦，初来乍到普林斯顿，语言尚且生疏，生活 不甚顺畅，因此，他不堪孤身独战，找了两个合作者，构成了一个被物理学家们称为不是十 分恰当的组合。 

Boris Podolsky 和 Nathan Rosen 是爱因斯坦在普林斯顿高等研究院的助手。1935 年 3 月，Physics Review 杂志上发表了他们和爱因斯坦署名的 EPR 论文。文章中描述了一个佯 谬，之后，人们就以署名的三位物理学家名字的第一个字母命名，称为“EPR 佯谬”。

 EPR 原文中使用粒子的坐标和动量来描述爱因斯坦构想的理想实验，数学表述非常复 杂。后来，波姆用电子自旋来描述 EPR 佯谬，就简洁易懂多了。EPR 论文中涉及到“量 子纠缠态”的概念。这个名词当时还尚未被爱因斯坦等 3 位作者采用。（“纠缠”的名字是 薛定谔在 EPR 论文之后不久，得意洋洋地牵出他那只可怖的猫时候，第一次提到的。）因 此，我们首先解释一下，何谓纠缠态？ 

读者应该还记得我们解释过的“量子叠加态”。叠加态这个概念一直贯穿在我们这系列 文章中，从薛定谔的猫，到双缝实验中有分身术的孙悟空，不都是这个匪夷所思的“叠加 态”在作怪吗？不过，此文之前对叠加态的解释，都是针对一个粒子而言的。如果把叠加态 的概念用于两个以上粒子的系统，就更产生出来一些怪之又怪的现象，那些古怪行为的专 利，就该归功于“量子纠缠态”。

 比如，我们考虑一个两粒子的量子系统。也就是说，有两个会分身的孙悟空同居一室， 会有些什么样的状况发生呢？所有的状况不外乎归于两大类，一类是：两对孙悟空互不搭 架，自己只和自己的分身玩。这种情况下的系统，可看作是由两个独立的粒子组成，没有产 生什么有意思的新东西。

 另一类情况呢，也就是两对孙悟空互相有关系的情况了。我们借用“纠缠”这个词来描 述它们之间的互相关联。也就是说，这种情形下，两对量子孙悟空‘互相纠缠’，难舍难分。 有趣的是，将来竟然有人出来证明说，这量子孙悟空之间亲密无间的程度，不是我等常人所 能理解的，可以超过我们这个‘经典’人间所能达到的任何境界，任何极限哦。于是，我们 18 只好叹息一声说：啊，这就是‘量子纠缠态’。 

爱因斯坦等三人提出的假想实验中，描述了两个粒子的互相纠缠：想象一个不稳定的大 粒子衰变成两个小粒子的情况，两个小粒子向相反的两个方向飞开去。假设该粒子有两种可 能的自旋，分别叫“左”和“右”，那么，如果粒子 A 的自旋为“左”，粒子 B 的自旋便一 定是“右”，以保持总体守恒，反之亦然。我们说，这两个粒子构成了量子纠缠态。 

用我们有关孙悟空的比喻将爱因斯坦的意思重复一遍：大石头中蹦出了两个孙悟空。每 个孙悟空都握着一根金箍棒。这金箍棒有一种沿着轴线旋转的功能：或者左旋，或者右旋。 两个孙悟空的金箍棒旋转方向互相关联：如果孙 A 的金箍棒为“左”旋，孙 B 的金箍棒便 一定是“右”旋，反之亦然。我们便说，这两个孙悟空互相纠缠。

大石头裂开了，两个互相纠缠的孙悟空（A 和 B）并不愿意同处一室，而是朝相反方向 拼命跑，它们相距越来越远，越来越远……。根据守恒定律，它们应该永远是“左右”关联 的。然后，如来佛和观音菩萨同时分别在天庭的两头，抓住了 A 和 B。根据量子论，只要 我们不去探测，每个孙悟空的金箍棒旋转方向都是不确定的，处在一种左/右可能性叠加的 混合状态（比如，各 50%）。但是，两个孙悟空被抓住时，A、B 金箍棒的叠加态便在一瞬 间坍缩了，比如说，孙悟空 A 立刻随机地作出决定，让其金箍棒选择“左”旋。但是，因 为守恒，孙悟空 B 就肯定要决定它的金箍棒为“右”旋。问题是，在被抓住时，孙悟空 A 和孙悟空 B 之间已经相隔非常遥远，比如说几万光年吧，它们怎么能够做到及时地互相通 信，使得 B 能够知道 A 在那一霎那的随机决定呢？除非有超距瞬时的信号（心灵感应）来 回于两个孙悟空之间！而这超距作用又是现有的物理知识不容许的。于是，这就构成了佯 谬。因此，EPR 的作者们洋洋得意地得出结论：波尔等人对量子论的几率解释是站不住脚的。

 此一时彼一时！这时的波尔，已经知己知彼、老谋深算。他深思熟虑地考虑了一阵之 后，马上上阵应战。很快就明白了，爱因斯坦的思路完全是经典的，总是认为有一个离开观 测手段而存在的实在世界。这个世界图像是和波尔代表的哥本哈根派的“观测手段影响结 果”的观点完全不一致的。玻尔认为，微观的实在世界，只有和观测手段连起来讲才有意 义。在观测之前，并不存在兩个客观独立的孫悟空实在。只有波函数描述的一个互相关联的 整体，并无相隔甚远的两个分体，既然只是协调相关的一体，它们之间无需传递什么信号！ 因此，EPR 佯谬只不过是表明了两派哲学观的差别：爱因斯坦的“经典局域实在观”和波 尔一派的“量子非局域实在观”的根本区别。 

当然，哲学观的不同是根深蒂固难以改变的。爱因斯坦绝对接受不了玻尔的这种古怪的 说法，即使在之后的二三十年中，玻尔的理论占了上风，量子論如日中天，它的各个分支高 速发展，给人类社会带来了伟大的技术革命。爱因斯坦仍然固执地坚持他的经典信念，站在 反对量子论的那边。

 刚才谈到的约翰·惠勒，曾经与波尔及爱因斯坦在一起工作过，被人称为“哥本哈根学 派的最后一位大师”，直到 2008 年去世，惠勒 90 多岁的高龄还在继续思考量子力学中的哲 学问题。记得惠勒曾引用玻尔的话说，“任何一种基本量子现象只在其被记录之后才是一种 19 现象”。意思就是说，比如我们上面说到的两个互相纠缠的孙悟空，在被抓住之前，它们到 底在哪里？离多远？是个什么模样？有没有金箍棒？金箍棒是左旋还是右旋？哥本哈根派认 为，这些全都是些无意义的、不该问的问题。还没有被如来佛和观音抓住之前，没有什么所 谓的“两个孙悟空”，它们并不是真实存在的东西！ 

惠勒对量子论的贡献是非同一般的。上世纪 80 年代初期，笔者有幸与惠勒博士在一 起工作，并准备和翻译当时他去中国访问的讲稿，那篇讲稿是基于他的一篇论文：“Law without Law”，后来，此讲稿由科大的方励之编著，1982 年出版，取名为《物理学和质朴 性 -没有定律的定律》。在讲稿中，惠勒提到他在 1979 年，为纪念爱因斯坦诞辰 100 周年的 普林斯顿讨论会上，提出的所谓“延迟选择实验”（delayed choice experiment）。这个“延 迟选择实验”，是我们讨论过的“电子双缝干涉”实验的一个令人吃惊的新版本。在新构想 中，惠勒戏剧化地将实验稍加改变，便可以使得实验员能在电子已经通过双缝之后，作出 “延迟决定”，从而改变电子通过双缝时的历史！这种十分怪异的，好像能从将来触摸到过 去的说法，量子论的哥本哈根派又如何解释呢？这个实验彻底地挑战了经典物理的因果律。

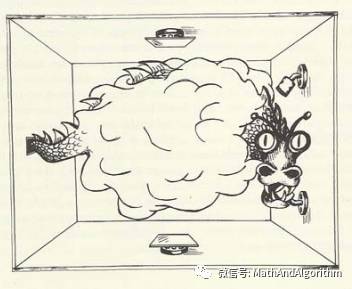
惠勒曾经用一个龙图来说明这一点。这个龙图也可以用费曼的路径积分观点来理解：龙 的头和尾巴对应于测量时的两个点，在这两点测量的数值是确定的。根据量子力学的路径积 分解释，两点之间的关联可以用它们之间的所有路径贡献的总和来计算。因为要考虑所有的 路径，因此，龙的身体就将是糊里糊涂的一片（如下图所示）。 

惠勒的龙：Field Gilbert 画，扫描自 Niels Bohr: A Centenary Volume(Harvard 1985)， p151. 

惠勒提出“延迟选择实验”时，已经到了 1979 年。早在 1964 年，出于捍卫爱因斯坦 EPR 论文的初衷，另一位杰出的英国物理学家，约翰 • 斯图尔特 • 贝尔（John Stewart Bell），就已经帶著他的“貝爾不等式”，潇洒登場了。

作者：张天蓉

编辑：Gemini

来源：blog.sciencenet.cn/u/tianrong1945

第一章：量子纠缠（一）——薛定谔、女朋友、猫

第二章：量子纠缠（二）——男孩物理学

第三章：量子纠缠（三）——上帝掷骰子吗
第四章：量子纠缠（三）——波尔和爱因斯坦之争

未完待续！

---

☞  哈尔莫斯：怎样做数学研究

☞  扎克伯格2017年哈佛大学毕业演讲

☞  线性代数在组合数学中的应用

☞  你见过真的菲利普曲线吗？

☞  支持向量机(SVM)的故事是这样子的

☞  深度神经网络中的数学，对你来说会不会太难？

☞  编程需要知道多少数学知识？

☞  陈省身——什么是几何学

☞  模式识别研究的回顾与展望

☞  曲面论

☞  自然底数e的意义是什么？

☞  如何向5岁小孩解释什么是支持向量机（SVM）？

☞  华裔天才数学家陶哲轩自述

☞  代数，分析，几何与拓扑，现代数学的三大方法论

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域。

稿件一经采用，我们将奉上稿酬。

投稿邮箱：[email protected]