你不知道的数学趣闻(一)
本期介绍的你可能不知道的数学趣闻有:
数学神童维纳的年龄
海盗分金问题
灌水问题
一封数学情书
完美正方形
数学神童维纳的年龄
20世纪著名数学家诺伯特·维纳,从小就智力超常,三岁时就能读写,十四岁时就大学毕业了。几年后,他又通过了博士论文答辩,成为美国哈佛大学的科学博士。
在博士学位的授予仪式上,执行主席看到一脸稚气的维纳,颇为惊讶,于是就当面询问他的年龄。维纳不愧为数学神童,他的回答十分巧妙:“我今年岁数的立方是个四位数,岁数的四次方是个六位数,这两个数,刚好把十个数字0、1、2、3、4、5、6、7、8、9全都用上了,不重不漏。这意味着全体数字都向我俯首称臣,预祝我将来在数学领域里一定能干出一番惊天动地的大事业。”
维纳此言一出,四座皆惊,大家都被他的这道妙题深深地吸引住了。整个会场上的人,都在议论他的年龄问题。
其实这个问题不难解答,但是需要一点数字“灵感”。不难发现,21的立方是四位数,而22的立方已经是五位数了,所以维纳的年龄最多是21岁;同样道理,18的四次方是六位数,而17的四次方则是五位数了,所以维纳的年龄至少是18岁。这样,维纳的年龄只可能是18、19、20、21这四个数中的一个。
剩下的工作就是“一一筛选”了。20的立方是8000,有3个重复数字0,不合题意。同理,19的四次方等于130321,21的四次方等于194481,都不合题意。最后只剩下一个18,是不是正确答案呢?验算一下,18的立方等于5832,四次方等于104976,恰好“不重不漏”地用完了十个阿拉伯数字,多么完美的组合!
这个年仅18岁的少年博士,后来果然成就了一番大事业:他成为信息论的前驱和控制论的奠基人。
海盗分金问题
经济学上有个“海盗分金”模型:是说5个海盗抢得100枚金币,他们按抽签的顺序依次提方案:首先由1号提出分配方案,然后5人表决,超过半数同意方案才被通过,否则他将被扔入大海喂鲨鱼,依此类推。“海盗分金”其实是一个高度简化和抽象的模型,体现了博弈的思想。在“海盗分金”模型中,任何“分配者”想让自己的方案获得通过的关键是事先考虑清楚“挑战者”的分配方案是什么,并用最小的代价获取最大收益,拉拢“挑战者”分配方案中最不得意的人们。
有兴趣的同学可以试着推理一下哦~
灌水问题
公园水池每周需换一次水.水池有甲、乙、丙三根进水管.第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开小1时,恰好在打开某根进水管1小时后灌满空水池.第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,灌满一池水比第一周少用了15分钟;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时,比第一周多用了15分钟.第四周他三个管同时打开,灌满一池水用了2小时20分,第五周他只打开甲 管,那么灌满一池水需用________小时
一封数学情书
当你学好数学后,写出的情书应该是这样的
甚至这样的
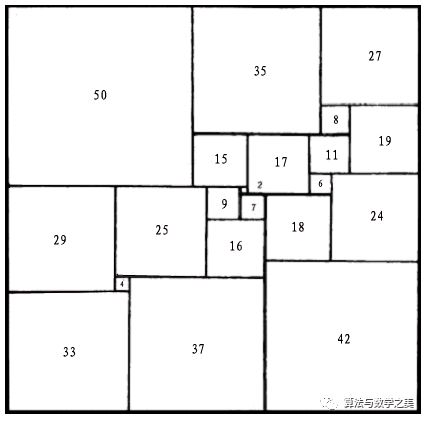
完美正方形
“完美正方形”是指在一正方形内切割出大小都相异的小正方形。此概念最早由莫伦提出,完美正方形的最小阶数为21阶。
数学家们一度花了很大精力都无任何结果,以至于1930年苏联著名数学家鲁金猜想,不可能把一个正方形分割成有限个大小不同的正方形。
莫伦对此猜想提出了挑战,并提供了一个解决思路:如果同一个矩形有两个不同的正方形剖分,且其中一个剖分的每个正方形都不同于另一个剖分的每个正方形,那么,这两个剖分再添上两个正方形(它异于两个剖分中的任何一个正方形),便可构造出一个完美正方形。而在此之前,完美矩形已经有了比较丰富的成果。
1939年,斯普拉格按照莫伦的构想成功地构造出一个55阶的完美正方形,其边长为4205。
几个月后,阶数更小(28阶)、边长更短(1015)的完美正方形由剑桥大学三一学院的四位大学生构造出来。
1948年,威尔科克斯构造出24阶完美正方形,但其中含有一个完美矩形(此类正方形被称为混完美正方形。完全由正方形构造成的正方形称为纯完美正方形)。一直到1978年,这个纪录才被打破。
1967年,威尔森构造成功25阶、26阶完美正方形。
1962年,荷兰特温特技术大学的杜伊维斯廷证明:不存在20阶以下的完美正方形。
1978年,杜伊维斯廷借助计算机技术,成功地构造出一个21阶的完美正方形,它是唯一的,且它不仅阶数最低,同时数字也更简单,此外构造上它也有许多优美的特点,比如2的某些次幂恰好位于一条对角线上,等等。
杜伊维斯廷同时还证明了:低于21阶的完美正方形不存在。
1982年,杜伊维斯廷又证明了:不存在低于24阶的混完美正方形。
1992年,布卡姆和杜伊维斯廷给出了21~25阶全部207个纯完美正方形:
阶数 21 22 23 24 25
个数 1 8 12 26 160
至此,完美正方形的讨论暂时画上一个句号。但数学家的研究并没有止,他们又研究了不同大小正方形是否可以填充整个平面的问题,此外他们还将完美剖分的问题推广到莫比乌斯带、圆柱面、环面和克莱茵瓶上,也取得了许多有趣的成果。
但是立方体填充被证明是没有的。
————
编辑 ∑Gemini
来源:明达之音-西电数统院
☞泰勒定理的奇闻轶事
☞丘成桐:漫谈微分几何
☞Leibniz 如何想出微积分?(一)
☞线性相关和秩的物理意义
☞数学史上你认为最丑陋的公式是什么?
☞陶哲轩谈什么是好的数学
☞田渊栋:数学的用处(下篇)
☞你绝对没想过原来数学家这么流氓,一言不合就进行暴力证明
☞世界上最牛的五篇博士论文
☞数学中有哪些巧合让人眼前一亮?
☞算法立功!清华毕业教授美国被抢车,警察无能为力自己用“贪心算法”找回
☞学术史上的奇文:怎样用数学抓狮子
☞台大教授的反思:最难的一课 我们却没教给学生
☞麻省理工学院(MIT)研究生学习指导—— 怎样做研究生
☞分享 数学,常识和运气 ——投资大师詹姆斯·西蒙斯2010年在MIT的讲座
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域,经采用我们将奉上稿酬。
投稿邮箱:[email protected]