匹配多个字符串——AC自动机

真·AC自动机：zyy
AC自动机这个东西。。名字真的是没得吐槽=_=
它运用了kmp算法的next思想（体现于后文的fail指针）以及trie的数据结构（字母树）
kmp如果不会的话还可以，trie不会的话。。建议还是先去学trie吧
我看了好久。。才看懂这个蜜汁自动机

---

先看一下模版题来了解AC自动机的用处：
Hdu2222
题意：有n段小字符串，求其中有多少段出现在了一个大字符串中
题目应该不难理解
那么怎么做？
朴素想法：每一个字符串去大字符串中kmp一遍之间效率O（n*len）
。。妥妥tle

对于这种问题，我们就需要用到AC自动机
AC自动机=trie+fail
所谓fail指针，就是一个类似于kmp中的next，用于匹配失败时快速跳转。
虽然不知道为什么别的为什么每个例子都一样。。那我也一样好了
大概是什么 she he shr say her..??
然后大字符串： yasheshr？
差不多就这样…
我们先把所有小字符串放到trie中，这一步不详细解释了

inline void insert(string ts)
{
    int len=ts.length();
    int p=0;
    For(i,0,len-1)
    {
        int c=ts[i]-'a';
        if(!nxt[p][c])  nxt[p][c]=++tot;
        p=nxt[p][c];
    }
    cnt[p]++;
}

接下来我们考虑一下大字符串在trie上的询问
一条一条走下去。。走不了了就回溯？
累加各个结束标记？
时间效率。。O（结点数）
好像和直接kmp没什么太大局别- -…
但是其实有很多回溯都是没有用的
很多很多！！
不只是这样
我们根据刚才的输入构建出来的trie应该是这样的：

我们搜完she后,如果是用回溯，就会找不到r在哪=_=
所以不只是时间上，连思想上都退化成了枚举。。
那么要怎么办？
我们可不可以在搜完she后直接跳到he后面那个r呢
。。。这个想法似曾相识对吧= =
没错它就是kmp
fail指针就是这个用处，直接指向he后面那个r
这个其实。。说实话，构造过程只可意会不可言传
好吧我还是言传一下 不然要被打
一开始，所有节点的fail指针指向root(根节点）
我们如果要更新节点t的fail，那么我们就沿着t的父亲的fail指针一直走啊走，走到一个节点有t这个字母的儿子
比如说我们要找上图h的fail

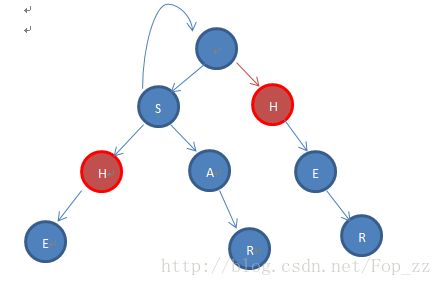
我们通过S的fail询问到根节点，发现其有一个是叫做 H的儿子
那么我们就把第三层的h的fail指向第二次的那个h

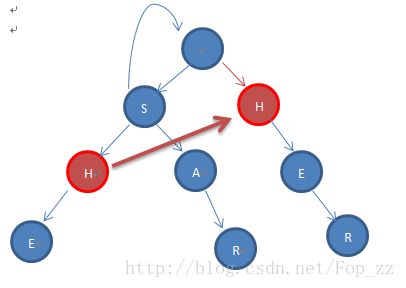
同样，我们要找E的fail

通过E的父节点H的fail，找到第二层的H，发现其有一个儿子为E，就可以更新fail指针了

啊。。吐血
还是看代码理解一下吧，这个真的不知道应该怎么说
补：lc233大佬说，为什么不能用dfs求，那么下面我放两张图大家理解一下。。

然后我们要求最深的那个E的fail
此时更新了第一条链的fail

这就是为什么dfs不可行。。。

inline void build()
{
    int t,l=1,r=1;
    fail[root]=0;
    q[1]=root;
    while(l<=r)
    {
        t=q[l];
        int p=0;
        For(i,0,25)
        {
            if(nxt[t][i])
            {
                if(t==root){fail[nxt[t][i]]=root;}
                else
                {
                    p=fail[t];
                    while(p)
                    {
                        if(nxt[p][i])
                        {
                            fail[nxt[t][i]]=nxt[p][i];
                            break;
                        }
                        p=fail[p];
                    }

                    if(!p)  
                    {
                        if(nxt[p][i]) fail[nxt[t][i]]=nxt[p][i];
                        else fail[nxt[t][i]]=root;
                    }
                }
                q[++r]=nxt[t][i];
            }
        }
        l++;
    }
    For(i,1,r)  q[i]=0;
}

然后询问的时候，我们只需要一路搜下去，如果匹配失败就往fail那边跑，一路把结束标记全部加起来。。就是答案了
要注意！重复的千万不能加！
当我们加到一个点时，可以用一个while循环将他所有fail指针上的end指针加上去

inline void query(string s)
{
    int len=s.length(),sum=0,p=0;
    For(i,0,len-1)
    {
        int c=s[i]-'a';
        while(nxt[p][c]==0&&p)  p=fail[p];
        p=nxt[p][c];
        int t=p;
        while(t&&cnt[t]!=-1)
        {
            sum+=cnt[t];
            cnt[t]=-1;
            t=fail[t];
        }
    }
    printf("%d\n",sum);
}

好了那么大致思路就是这样了
附HDU2222 AC代码

#include
#include
#include
#include
#include
#include
#include
#define inf 1e9
#define ll long long
#define For(i,j,k) for(int i=j;i<=k;i++)
#define Dow(i,j,k) for(int i=k;i>=j;i--)
using namespace std;
int n,nn,nxt[1000001][30],q[1000001],fail[1000001],cnt[1000001],tot,root=0;
inline void insert(string ts)
{
    int len=ts.length();
    int p=0;
    For(i,0,len-1)
    {
        int c=ts[i]-'a';
        if(!nxt[p][c])  nxt[p][c]=++tot;
        p=nxt[p][c];
    }
    cnt[p]++;
}
inline void build()
{
    int t,l=1,r=1;
    fail[root]=0;
    q[1]=root;
    while(l<=r)
    {
        t=q[l];
        int p=0;
        For(i,0,25)
        {
            if(nxt[t][i])
            {
                if(t==root){fail[nxt[t][i]]=root;}
                else
                {
                    p=fail[t];
                    while(p)
                    {
                        if(nxt[p][i])
                        {
                            fail[nxt[t][i]]=nxt[p][i];
                            break;
                        }
                        p=fail[p];
                    }

                    if(!p)  
                    {
                        if(nxt[p][i]) fail[nxt[t][i]]=nxt[p][i];
                        else fail[nxt[t][i]]=root;
                    }
                }
                q[++r]=nxt[t][i];
            }
        }
        l++;
    }
    For(i,1,r)  q[i]=0;
}
inline void query(string s)
{
    int len=s.length(),sum=0,p=0;
    For(i,0,len-1)
    {
        int c=s[i]-'a';
        while(nxt[p][c]==0&&p)  p=fail[p];
        p=nxt[p][c];
        int t=p;
        while(t&&cnt[t]!=-1)
        {
            sum+=cnt[t];
            cnt[t]=-1;
            t=fail[t];
        }
    }
    printf("%d\n",sum);
}
inline void doit()
{
    For(i,0,tot)
        For(j,0,25) nxt[i][j]=0;
    For(i,0,tot)    fail[i]=cnt[i]=0;
    tot=root=0;
    cin>>n;
    For(i,1,n)
    {
        string ts;
        cin>>ts;
        insert(ts);
    }
    build();
    string s;
    cin>>s;
    query(s);
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>nn;
    For(ii,1,nn)
    {
        doit();
    }
}