Deep Reinforcement learning - Policy Gradient+PPO+TRPO

生物进化过程中为适应环境而进行的学习有两个特点

• 人从来不是静止的被动等待而是主动的对环境进行试探
• 环境对于人的试探动作产生一个反馈，人根据环境的反馈来调整以后的行为，是一种从环境状态到行为映射的学习

因此从自然界中的种种规律中得到启发，便有了强化学习。强化学习（Reinforcement Learning，RL）又被称为再励学习、增强学习，是指从环境状态到行为映射的学习，以使系统行为从环境中获得的累计奖励值最大的一种机器学习方法。

而所谓的深度强化学习是将强化学习和深度学习结合在一起，用强化学习来定义问题和优化目标，用深度学习来解决状态表示、策略表示等问题。两种不同的结合强化学习和深度学习的方式，分别用深度神经网络来建模强化学习中的值函数、策略，然后用误差反向传播算法来优化目标函数。因此可以有Deep Reinforcement Learning = RL + DL.

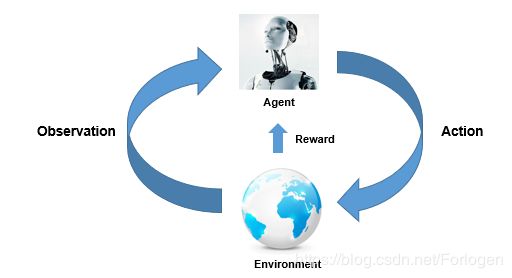
那如何简单的理解RL呢？在RL中有几个基本的概念:

• $Agent$：表示当前学习的主体
• $environment$：表示与Agent交互的对象
• $S$：表示环境的状态，$S_t$就表示$t$时刻环境状态集中的某一个状态
• $A$：表示个体的动作，$A_t$就表示$t$时刻Agent的动作集中的某一个动作
• $R$：表示采取某个动作后环境所给予的奖励，$t$时刻Agent在状态为$S_t$的前提下采取动作$A_t$所得到的的奖励$R_{t+1}$会在$t+1$时刻得到
• $\pi$：表示策略（policy）,Agent会根据$\pi$来选择某一个动作，即根据条件概率$\pi (a|s)$来在状态为$s$时选择动作$a$
• $\gamma$：表示折扣因子，当$\gamma$接近于0时，表示Agent更在意当下时刻的奖励，当$\gamma$接近于1时，表示Agent更在意长期奖励
• $P_{s{s}^{\prime }}^a$：表示在状态$s$时采取动作$a$会转换到状态$s^{\prime }$的概率
• $ϵ$：表示探索率，即在某个时刻Agent会以概率$ϵ$不选择当前迭代价值最大的动作，而是选择其他的动作
  

下面通过几个简单的例子进行一下阐述。假设Agent这里是一个孩子，environment为母亲，当孩子把水打翻时，母亲就会生气，并且会扣掉他的零花钱；那么孩子在观察到母亲的状态后就知道这样是不对的，那么他就会去把水擦干净，母亲此时就会变得开心，并多给他零花钱。因此经过多个这样的过程，孩子就知道不应该把水打翻或是打翻后要及时的擦干净，这样他就会获得最大的奖励。

那么RL和supervised learning有什么区别呢，以下图为例进行说明。假设我们现在在下围棋，如果当前为上面的盘势时，我们就要在（5，5）落子；当是下面的盘势时，就需要在（3，3）落子。这一切的操作都是在有指导或是在有标签的数据集上进行的，但是更多时候人类也无法确定在某种盘势下怎样落子是最优的，因此就需要强化学习。RL不需要根据标签来进行学习，它会不断地进行对弈来学习可以获取到最大累计奖励的落子策略，但是学习到一个很好的策略往往需要进行极多次的对弈。例如在AlphaGo中就是先使用supervised learning学习一个较好的网络，然后再使用两个网络进行对弈，最后得到一个足以打败人类的模型。

RL在近些年来受到了极大的关注，比较有名的便是Google的AlphaGo、AlphaZero和AlphaMaster，此外还有就是用来打电玩的OpenAI Five。

下面就跟着李宏毅老师的深度强化学习-2018课程的PPT来做一个总结。当然还有很多其他的课程，仅供参考：

David Silver深度强化学习课程
2018 年秋季伯克利大学CS 294-112 《深度强化学习课程》

为了表述一致，下面统一使用Actor来替代Agent。

策略$\pi$使用参数为$\theta$的神经网络进行表示，它的输入是机器所观察的当前的状态，通过表示为向量或是矩阵的形式，输出就是下一时刻应该采取的动作。比如在小蜜蜂这个游戏中，输入就是当前的游戏画面，可以将其表示一个三维的张量输入到网络中，输入表示可以采取的动作的概率分布，通过选择的表示概率最大的动作

然后在每一次采取动作后Actor都会得到一个奖励$r$，$r$的值可能是正的、负的或是0，取决下一时刻的情况。经过非常多次的游戏，我们希望Actor所获得的累计奖励$R={\sum }_{t=1}^T{r}_t$最大。

下面我们将Actor状态的变换过程按时刻顺序展开，如下所示：在状态为$s_i$时，Actor会采取动作$a_i$，状态下一时刻就会转换到$s_{t+1}$。这个过程可以表示为$\tau =\left\{s_1,a_1,s_2,a_2,\cdots ,s_T,a_T\right\}$，那么这一过程出现的概率可表示为:$$\begin{array}{l}{p}_{\theta }(\tau )\\ =p\left(s_1\right)p_{\theta }\left(a_1|s_1\right)p\left(s_2|s_1,a_1\right)p_{\theta }\left(a_2|s_2\right)p\left(s_3|s_2,a_2\right)\cdots \\ =p\left(s_1\right){\prod }_{t=1}^T{p}_{\theta }\left(a_t|s_t\right)p\left(s_{t+1}|s_t,a_t\right)\end{array}$$其中每一时刻状态的变化都依赖于前一时刻的状态，这样的过程类似于马尔科夫决策过程，更详细的的内容可参见强化学习（二）马尔科夫决策过程(MDP)

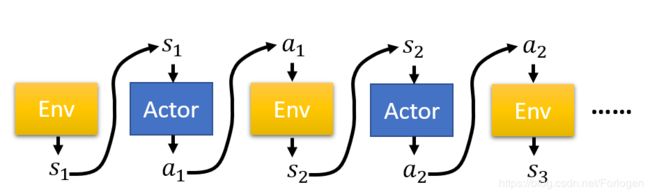
如果在每一次动作的选择后给与Actor一个奖励,那么整个过程如下所示:

用$R(\tau )={\sum }_{t=1}^T{r}_t$l来表示累计奖励,那么目标就是求得奖励期望${\overline{R}}_{\theta }={\sum }_{\tau }R(\tau )p_{\theta }(\tau )=E_{\tau \sim p_{\theta }(\tau )}[R(\tau )]$值最大。求解这个优化问题就需要用到梯度上升法，这里求解的梯度也称为策略梯度（Policy Gradient）。那么如何求解梯度$\nabla {\overline{R}}_{\theta }$呢？$\nabla {\overline{R}}_{\theta }$可写成如下的形式$$\nabla {\overline{R}}_{\theta }=\sum _{\tau }R(\tau )\nabla p_{\theta }(\tau )=\sum _{\tau }R(\tau )p_{\theta }(\tau )\frac{\nabla p_{\theta }(\tau )}{p_{\theta }(\tau )}$$因为前一项表示奖励，并不涉及梯度的求解，所以求梯度只针对后一项。而且先除再乘一个相同的值并不改变值得大小。根据$\nabla f(x)=f(x)\nabla \log f(x)$可将上式转换为$\nabla {\overline{R}}_{\theta }={\sum }_{\tau }R(\tau )p_{\theta }(\tau )\nabla \log p_{\theta }(\tau )$。

因为有$P(\tau |\theta )=p(s_1){\prod }_{t=1}^{T}p(a_t|s_t,\theta )p(r_t,s_{t+1}|s_t,a_t)$，取对数有$$P(\tau |\theta )=\log p\left(s_1\right)+\sum _{t=1}^T\log p\left(a_t|s_t,\theta \right)+\log p\left(r_t,s_{t+1}|s_t,a_t\right)$$而第一项和第三项均与求解梯度无关，因此有$\nabla \log P(\tau |\theta )={\sum }_{t=1}^T\nabla \log p\left(a_t|s_t,\theta \right)$，为了表述简单，统一不再写参数$\theta$。因此关于$\nabla {\overline{R}}_{\theta }$的式子可进一步转换为$$\begin{array}{rl}\nabla {\overline{R}}_{\theta }& =E_{\tau \sim p_{\theta }(\tau )}\left[R(\tau )\nabla \log p_{\theta }(\tau )\right]\approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)\nabla \log p_{\theta }\left({\tau }^n\right)\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\end{array}$$

最后根据梯度更新公式$\theta \leftarrow \theta +\eta \nabla {\overline{R}}_{\theta }$进行参数更新。如果策略${\tau }^n$在状态$s_t^n$时选择动作$a_t^n$时的奖励$R_{\tau }^n$为正时，就调整$\theta$增加$p(a_t^n|s_t^n)$，如果奖励为负值则需要减少$p(a_t^n|s_t^n)$。

但有时在某种具体的任务中，奖励值总是为正时，就需要做一些改变$$\nabla {\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\left(R\left({\tau }^n\right)-b\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)$$但是$b$的值需要自己设定，通常使用$b\approx E[R(\tau )]$。另外在某个时刻$t$采取动作后不会对于之前的奖励值造成影响，因此只需要关注这个时刻之后的情况，所以关于$\nabla {\overline{R}}_{\theta }$的式子可写为$$\nabla {\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\left(\sum _{t^{\prime }=t}^{T_n}{r}_{t^{\prime }}^n-b\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)$$此外当对于不同时刻的奖励加上折扣因子时，上式进一步的可变为$$\nabla {\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\left(\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{{}^{\prime }}}^n-b\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)$$

上面所讲的策略梯度属于on-policy的类别，此外还有off-policy的方法。那么两者之间如何区分呢？

• on-policy：它指的是我们需要学习的Agent和训练过程中和环境进行交互的Agent是同一个
• off-policy：它指的是我们需要学习的Agent和训练过程中真正和环境进行交互的Agent不是同一个

那么为什么会用到off-policy的策略，或者说on-policy的策略具有什么样的问题呢？虽然策略梯度在很多的RL任务中可以取得不错的效果，但是同样有一些难度。因为这样的方法对于迭代步骤次数十分的敏感：如果选的太小，训练过程将会极其的缓慢；如果选择的太大，反馈信号将会淹没在噪声中，甚至会让模型的效果雪崩式的下降。另外这样的方法采样的效率也很低，即使学习一个简单的任务也需要百万级乃至十亿级的总迭代次数。为了解决这些问题，研究者就提出了off-policy的策略，我们希望利用${\pi }_{{\theta }^{\prime }}$来进行采样，使用采样得到的样本来训练$\theta$所表示的Agent，这样采样得到的样本就可以被重复的使用。

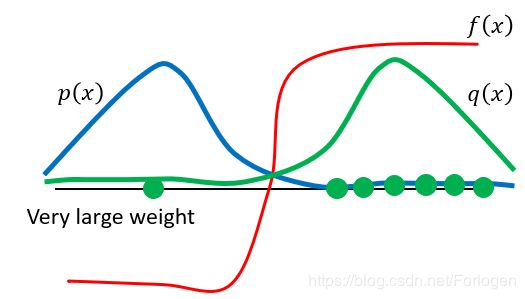
在介绍具体的内容之前，我们先看一个很有用的工具重要性采样（Importance sampling），它是使用一种分布来逼近所求分布的一种方法。假设我们想要求取目标分布$p$下的函数$f(x)$所满足的分布，如果$p$可以直接采样，那么使用蒙特卡洛方法有如下的计算$$E_{x\sim p}[f(x)]={\int }_{x}p(x)f(x)d_x\approx \frac{1}{N}\sum _{x_i\sim p,i=1}^{N}f\left(x_i\right)$$ 但是如果无法直接对$p$进行采样，那么上面的方法就不能使用了，这时就可以使用可以进行采样的分布$q$来近似$p$，计算公式为$$E_{x\sim p}[f(x)]={\int }_{x}p(x)f(x)d_x=E_{x\sim p^{\prime }}\left[\frac{p}{p^{\prime }}f(x)\right]\approx \frac{1}{N}\sum _{x_i\sim p^{\prime },i=1}^N\frac{p(x)}{p(x{)}^{\prime }}f(x)$$而且这里使用的分布$q$不应该和$p$相差太大，直观上我们可以理解所用分布自然不能和所要逼近的分布有太大的差距，否则就无法说的通了。下面从均值和方差的角度来看一下为什么要这样，从上面的式子中可以看出$E_{x\sim p}[f(x)]=E_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]$，它们的均值不会有太大差别。将两者的方差写为${\mathrm{Var}}_{x\sim p}[f(x)]$和${\mathrm{Var}}_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]$，根据概率论中方差和均值的转换公式有$$\begin{array}{l}{\mathrm{Var}}_{x\sim p}[f(x)]=E_{x\sim p}\left[f(x{)}^2\right]-{\left(E_{x\sim p}[f(x)]\right)}^2\\ {\mathrm{Var}}_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]=E_{x\sim q}\left[{\left(f(x)\frac{p(x)}{q(x)}\right)}^2\right]-{\left(E_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]\right)}^2\\ =E_{x\sim p}\left[f(x{)}^2\frac{p(x)}{q(x)}\right]-{\left(E_{x\sim p}[f(x)]\right)}^2\end{array}$$从中可以看出如果两者相差太大，就会导致$\frac{p(x)}{q(x)}$的值太大或是太小，从而导致两个分布之间的差别太大。下面通过图像可视化的理解以下上述的问题，蓝色实线表示分布$p(x)$，绿色实线表示真实采样的分布$q(x)$。从图中可以看出两者的分布是相反的，如果使用这样的$q(x)$去逼近$p(x)$，$q(x)$在右面奖励为正的部分采样的概率更大，因此大部分情况下奖励值均是大于零的，可能会在左边采样导致结果符合真实情况，但是因为概率太小，要达到这样的结果往往需要采样很多次，这样耗费的时间将会很多，因此两者之间的差别不应该太大。

因此off-policy的梯度求解式为$\nabla {\overline{R}}_{\theta }=E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}\left[\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}R(\tau )\nabla \log p_{\theta }(\tau )\right]$，使用${\pi }_{{\theta }^{\prime }}$采样得到的样本来训练$\theta$。

在on-policy策略下梯度计算为：$$\begin{array}{rl}\nabla {\overline{R}}_{\theta }& =E_{\left(s_t,a_t\right)\sim {\pi }_{\theta }}\left[A^{\theta }\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]\\ & =E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{P_{\theta }\left(s_t,a_t\right)}{P_{{\theta }^{\prime }}\left(s_t,a_t\right)}{A}^{\theta }\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]\\ & =E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}\frac{p_{\theta }\left(s_t\right)}{p_{{\theta }^{\prime }}\left(s_t\right)}{A}^{\theta }\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]\end{array}$$

因为此时是从${\pi }_{{\theta }^{\prime }}$中进行采样，因此应使用$A^{{\theta }^{\prime }}\left(s_t,a_t\right)$代替$A^{\theta }\left(s_t,a_t\right)$，而且$\frac{p_{\theta }(s_t)}{p_{{\theta }^{\prime }}(s_t)}$值应接近1，同时为了方便计算，可以将其去掉。最后求解的表达式为$$J^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]$$

那么如何求解上式呢？下面简单介绍两种方法，分别是TRPO (Trust Region Policy Optimization)和Proximal Policy Optimization (PPO)

PPO由OpenAI提出，为了使得两个分布不要差别太大，这里使用了KL散度来表示两个分布间行为的差别（而不是参数的差别）。当分布间差别越大时，施加到目标函数上的惩罚就越大，反之越小，惩罚的程度由超参数$\beta$控制。$$\begin{array}{c}{J}_{PPO}^{{\theta }^{\prime }}(\theta )=J^{{\theta }^{\prime }}(\theta )-\beta KL\left(\theta ,{\theta }^{\prime }\right)\\ J^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]\end{array}$$

TRPO同样使用了KL散度，但不同于PPO的是它并没有把KL散度直接合并到目标函数中，而是作为了一种限制，这也导致了它比较难计算，因此实际中使用的并不多。$$J_{TRPO}^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]$$

PPO的算法流程为：

• 初始化policy的参数${\theta }^0$
• 在每一次迭代中,使用${\theta }^k$与环境互动，收集状态和行动并计算对应的$A^{{\theta }^k}\left(s_t,a_t\right)$
• 不断更新参数，找到目标函数$J_{PPO}^{{\theta }^k}(\theta )=J^{{\theta }^k}(\theta )-\beta KL\left(\theta ,{\theta }^k\right)$最优值对应的参数$\theta$

PPO的优点：PPO 算法很好地权衡了实现简单性、样本复杂度和调参难度，它尝试在每一迭代步计算一个更新以最小化成本函数，在计算梯度时还需要确保与先前策略有相对较小的偏差。

还有一个针对与PPO的改进算法PPO2，它的目标函数为$$J_{PPO2}^{{\theta }^k}(\theta )\approx \sum _{\left(s_t,a_t\right)}\min \left(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}{A}^{{\theta }^k}\left(s_t,a_t\right),\mathrm{clip}\left(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)},1-\epsilon ,1+\epsilon \right)A^{{\theta }^k}\left(s_t,a_t\right)\right)$$它使用了$clip(.)$来控制分布间的差别。

参考

TRPO和PPO（上）
策略梯度下降过时了，OpenAI 拿出一种新的策略优化算法PPO
Proximal Policy Optimization Algorithm
Trust Resgion Policy Optimization
Sample Efficient Actor-Critic with Experience Replay
RL — Policy Gradient Explained
强化学习(十三) 策略梯度(Policy Gradient)