监督学习——通用线性模型

一、何谓监督学习

要给出监督学习准确的定义并不容易，因为每本参考资料中都给出了不同的解释，虽然核心的思想是相同的， 但是再

写博客的时候， 总得选择自己满意的定义。 在监督学习这个概念上，我选择以李航老师的统计学习方法 中的定义作为

标准，监督学习(supervised learning)的任务是一个 学习模型，使模型能够对任意给定的输入， 对其相应的输出做出

一个好的预测（注意：这里的输入何输出， 是指某个系统的输入、输出，与学习的输入、输出不同）。

1 通用线性模型

首先我们要介绍的是一组用于回归的方法，“回归”一词源于最佳拟合，表示要找到最佳拟合参数集。在回归方法中，目标值被估计为输入变量的线性组合。在数学概念中，被称为估计值（predicted value）。线性的回归方程：

称为回归系数，称为截距。

1.1 普通最小二乘

线性回归（LinearRegression）模型的目标是拟合一个系数为的线性模型，使得观测变量的值与目标值之间的残差尽可能小。在数学中，它主要解决以下形式的问题：

线性回归把数组X，y的你和系数存储在成员变量coef_中：

>>> from sklearn import linear_model
>>> clf = linear_model.LinearRegression()
>>> clf.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> clf.coef_
array([ 0.5,  0.5])

然而，最小普通二乘系数的估计和模型的独立性相关，输入矩阵X的列有近似的线性关系时，最小普通二乘对观察到的数据的随错误估计非常敏感，这种情况下会产生较大的方差。

例子：

• Linear Regression Example

下面的例子仅仅使用了diabetes数据集中的第一特征，目的只是为了表明线性回归技术的二维的拟合图，从图中可以看出线性回归尽可能使数据集中观察到数据与预测数据之间的残差的平方最小。

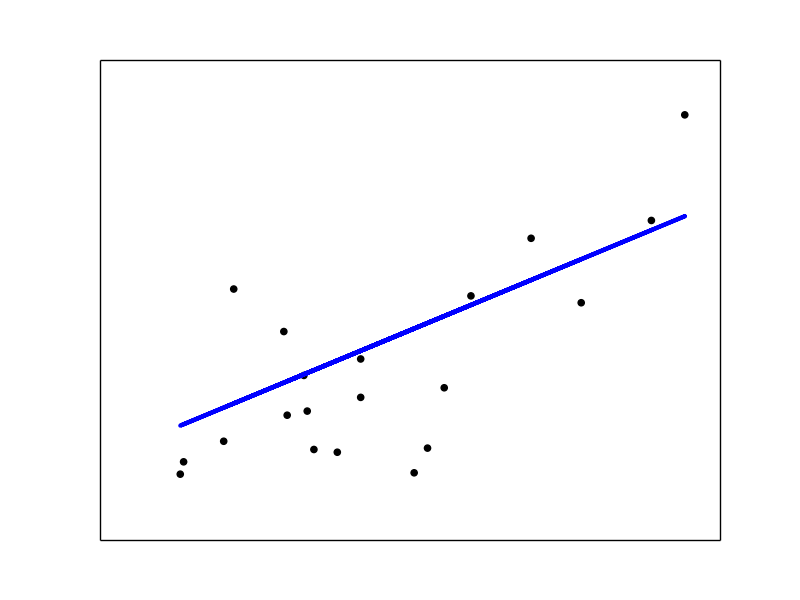
回归系数、残差平方、 Variance score的计算如下：

输出：
Coefficients:
 [ 938.23786125]
Residual sum of squares: 2548.07
Variance score: 0.47

print(__doc__)


# Code source: Jaques Grobler
# License: BSD 3 clause


import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model

# Load the diabetes dataset
diabetes = datasets.load_diabetes()


# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis]
diabetes_X_temp = diabetes_X[:, :, 2]

# Split the data into training/testing sets
diabetes_X_train = diabetes_X_temp[:-20]
diabetes_X_test = diabetes_X_temp[-20:]

# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]

# Create linear regression object
regr = linear_model.LinearRegression()

# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)

# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean square error
print("Residual sum of squares: %.2f"
      % np.mean((regr.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % regr.score(diabetes_X_test, diabetes_y_test))

# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, regr.predict(diabetes_X_test), color='blue',
         linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()

如果X是一个大小为n行p列的矩阵，假设n>=p，则线性回归的普通最小二乘的算法复杂度为。

1.2 岭回归（Ridge regression）

岭回归通过对回归系数增加一个惩罚因子解决了如下形式的普通最小二乘问题，岭回归系数使得残差平方和最小：

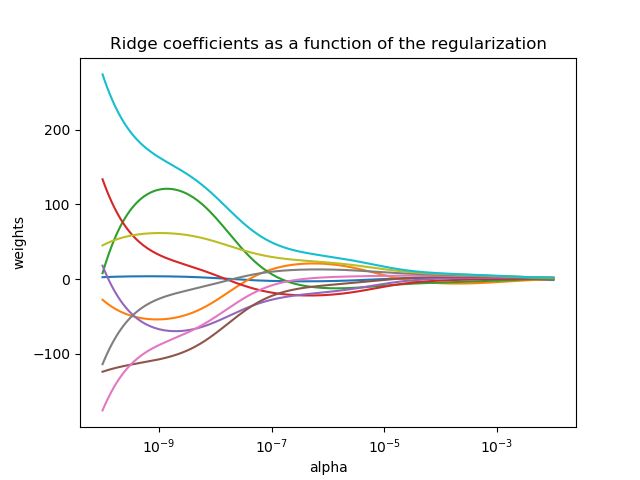
是一个控制收缩率大小的参数：越大，收缩率就越大，因此，回归线数的共线性就越健壮，图1给出了和权重weights之间的关系。

同其他线性模型一样，岭回归把数组X，y的你和系数存储在成员变量coef_中：

>>> from sklearn import linear_model
>>> clf = linear_model.Ridge (alpha = .5)
>>> clf.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
      normalize=False, solver='auto', tol=0.001)
>>> clf.coef_
array([ 0.34545455,  0.34545455])
>>> clf.intercept_
0.13636...

• Plot Ridge coefficients as a function of the regularization
• Classification of text documents using sparse features

岭回归的复杂度与线性回归复杂度一样。

1.2.1 设置正则化的参数：广义交叉验证

RidgeCV 的岭回归中实现了参数alpha的交叉验证。RidgeCV与GridSearchCV的实现原理一样，只是RidgeCV用的方法是广义交叉验证（GCV），而GridSearchCV则用的是一对一交叉验证（leave-one-out cross-validation）。

1.3 Lasso

Lasso是估计稀疏系数的线性模型。Lasso总是倾向于解决参数较少的问题，并可以有效的减少解决方案依赖的变量参数。为此，Lasso及其 变形

是压缩感知领域的基础，在特定的情况下，Lasso可以恢复非零权重的准确集合。

Lasso是由正则化参数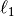组成的线性模型，目标函数为：

为常数，范数为参数向量的主题。

 Lasso使用梯度下降法拟合系数，另一种实现方法参考 Least Angle Regression 。

>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha = 0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,
   normalize=False, positive=False, precompute=False, random_state=None,
   selection='cyclic', tol=0.0001, warm_start=False)
>>> reg.predict([[1, 1]])
array([ 0.8])

例子:

• Lasso and Elastic Net for Sparse Signals
• Compressive sensing: tomography reconstruction with L1 prior (Lasso)

注意  使用Lasso进行特征选择

由于Lasso能够处理稀疏的线性模型，因此Lasso可以用做特征选择 ，详细请参见 L1-based feature selection。