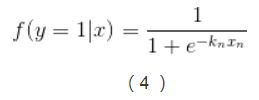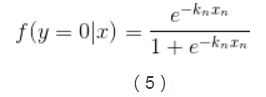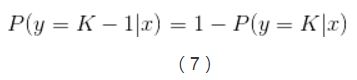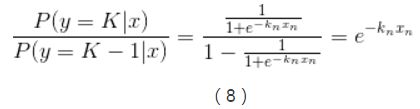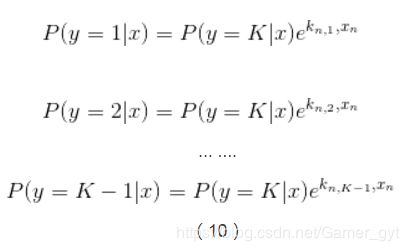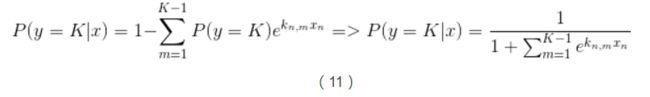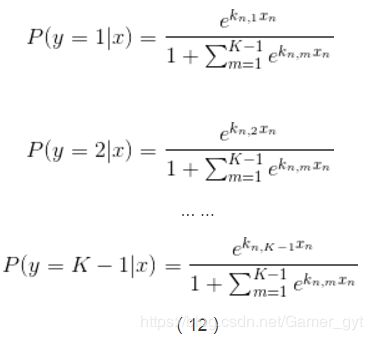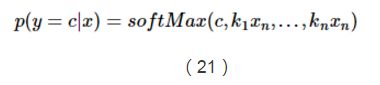多分类逻辑回归(Multinomial Logistic Regression)
打开微信扫一扫,关注微信公众号【搜索与推荐Wiki】
前言
分类从结果的数量上可以简单的划分为:
- 二分类(Binary Classification)
- 多分类(Multinomial Classification)。
其中二分类是最常见且使用最多的分类场景,解决二分类的算法有很多,比如:
- 基本的KNN、贝叶斯、SVM
- Online Ranking中用来做二分类的包括FM、FFM、GBDT、LR、XGBoost等
多分类中比如:
- 改进版的KNN、改进版的贝叶斯、改进版的SVM等
- 多类别的逻辑回归
啰嗦了这么多,其实就是为了说这个多分类的逻辑回归。
简介
在统计学里,多类别逻辑回归是一个将逻辑回归一般化成多类别问题得到的分类方法。用更加专业的话来说,它就是一个用来预测一个具有类别分布的因变量不同可能结果的概率的模型。
另外,多类别逻辑回归也有很多其它的名字,包括polytomous LR,multiclass LR,softmax regression,multinomial logit,maximum entropy classifier,conditional maximum entropy model。
在多类别逻辑回归中,因变量是根据一系列自变量(就是我们所说的特征、观测变量)来预测得到的。具体来说,就是通过将自变量和相应参数进行线性组合之后,使用某种概率模型来计算预测因变量中得到某个结果的概率,而自变量对应的参数是通过训练数据计算得到的,有时我们将这些参数成为回归系数。
模型分析
1、线性分类器
多分类逻辑回归使用的是跟线性回归一致的线性预测函数,其基本表达式如下:
其中i=[1,n]这里的k是一个回归系数,它表示的是第n个观测变量/特征对地n个结果的影响有多大。这里将1看做x0,我们可以得到上述公式的向量化形式:
这里kn是一个回归系数向量,表示的是观测向量xi表示的观测数据对结果k的影响度,或者叫重要性。
2、逻辑回归
多分类逻辑回归是基于逻辑回归(Logistic Regression)来做的,逻辑回归的基本表示如下:
其中y=1时,f(x)的表达式为:
则y=0时,f(x)的表达式为:
3、k-1个独立二元逻辑回归到多分类逻辑回归的扩展
实现多类别逻辑回归模型最简单的方法是,对于所有K个可能的分类结果,我们运行K−1个独立二元逻辑回归模型,在运行过程中把其中一个类别看成是主类别,然后将其它K−1个类别和我们所选择的主类别分别进行回归。通过这样的方式,如果选择结果K作为主类别的话,我们可以得到以下公式。
其推导过程如下:
这里有个假设的前提:y=K-1和y=K的概率和为1,即:
将逻辑回归的表达式带入可得:
公式两边同时求ln,可得:
在公式(6)中已经引入了所有可能的回归系数集合,对公式(6)两边进行指数化处理,能够得到以下公式:
因为所有概率的和为1,所以可以得到:
这样我们就能计算出所有给定未预测样本情况下某个结果的概率,如下:
回归参数的估计
上面篇幅所涉及到的每一个权重向量kn中的未知系数我们可以通过最大后验估计(MAP)来计算,同时也可以使用其它方法来计算,例如一些基于梯度的算法。
二元逻辑回归对数模型到多分类逻辑回归的扩展
在上文中提到了由K-1个独立二元回归到多分类逻辑回归的扩展,这里介绍另外一种多分类逻辑回归的扩展——使用线性预测器和额外的归一化因子(一个配分函数的对数形式)来对某个结果的概率的对数进行建模。
这里用一个额外项-ln(Z)来确保所有概率能够形成一个概率分布,从而使得这些概率的和等于1。
然后将等式两边的进行指数化,我们可以得到以下公式:
由于上面说到,所有概率之和等于1,因此我们可以得到Z的推导公式:
通过上边的公式进行计算,可得:
综合以上的公式,我们最后可以得到每一个结果对应的概率公式:
仔细观察的话,我们可以发现,所有的概率都具有以下形式:
我们可以把具有以下形式的函数成为softMax函数:
这个函数能够将x1,...,xn之间的差别放大,当存在一个xk比所有值中的最大值要小很多的话,那么它对应的softMax函数值就会区域0。相反,当xk是最大值的时候,除非第二大的值跟它很接近,否则的话softMax会趋于1。所以softmax函数可以构造出一个像是平滑函数一样的加权平均函数。
所以,我们可以把上面的概率公式写成如下softMax函数的形式:
至此,多分类的逻辑回归形式以及介绍完了,后续会进行最大似然函数的学习,敬请期待!