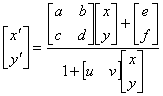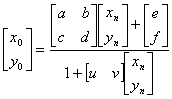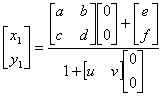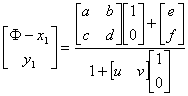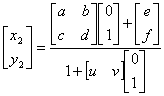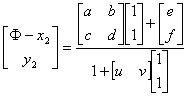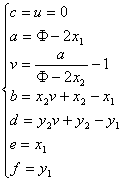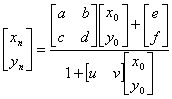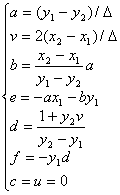数字图像处理:第六章 几何运算
第六章 几何运算
目录
- 引言
- 灰度级插值
- 空间变换
3.1 仿射变换
3.2 透视变换
- 几何校正
- 图象卷绕(Image Warping)
- 图象变形(Image Morphing)
作业
1.引言
几何运算与点运算不同,它可改变图象中物体(象素)之间的空间关系。这种运算可以看成将各象素在图象内移动的过程。其定义为:
g(x,y)=f(x',y')=f[a(x,y),b(x,y)] 其中,f(x,y)表示输入图象,g(x,y)表示输出图象,a(x,y)和b(x,y)表示空间变换,若它们是连续的,则将保持图象中的连通关系。
几何运算中灰度级插值是必不可少的组成部分,因为图象一般用整数位置处的象素来定义,而几何变换中,g(x,y)的灰度值一般由处在非整数坐标上的f(x,y)的值来确定,即g中的一个象素一般对应于f中的几个象素之间的位置。反过来看也是一样,即f中的一个象素往往被映射到g中的几个象素之间的位置。
实现几何运算有两种方法,其一为前向映射法,即:将输入象素的灰度一个个地转移到输出图象中,如果一个输入象素被映射到四个输出象素之间的位置,则其灰度值就按插值法在四个输出象素之间进行分配;其二为后向映射法(象素填充法),这时将输出象素逐个地映射回输入图象中,若输出象素被映射到四个输入象素之间的位置,则其灰度由它们的插值来确定。在实际中,通常采用后向映射法。
几何变换常用于摄象机的几何校正过程,这对于利用图象进行几何测量的工作是十分重要的。
仿射变换(Affine Transformation)和图象卷绕(Image Warping)是两类常见的几何运算。前者属于射影几何变换,多用于图象配准(ImageRegistration)作为比较或匹配的预处理过程;后者用控制点及插值过程来定义,将一幅图象逐渐变化到另一幅图象的图象变形(Morphing)过程是其典型的应用,多见于影视特技及广告的制作。
2.灰度级插值
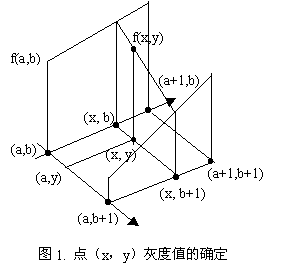
最简单的插值方法是最近邻插值,即选择离它所映射到的位置最近的输入象素的灰度值为插值结果。复杂一点的方法是双线性插值,如下图所示:
假设输出图象的宽度为W,高度为H,输入图象的宽度为w高度为h,要将输入图象的尺度拉伸或压缩变换至输出图象的尺度。按照线形插值的方法,将输入图象的宽度方向分为W等份,高度方向分为H等份,那么输出图象中任意一点(x,y)的灰度值就应该由输入图象中四点(a,b)、(a+1,b)、(a,b+1)和(a+1,b+1)的灰度值来确定(如图1.)。其中a和b的值分别为:
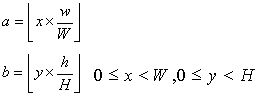 |
(x,y)点的灰度值f(x, y)应为:
其中
此外,还有多种其它插值方法,如三次样条等。图象处理软件一般都提供若干种插值方法供用户自己选择。
3.空间变换
空间变换包括可用数学函数表达的简单变换(如:平移、拉伸等仿射变换)和依赖实际图象而不易用函数形式描述的复杂变换(如对存在几何畸变的摄象机所拍摄的图象进行校正,需要实际拍摄栅格图象,根据栅格的实际扭曲数据建立空间变换;再如通过指定图象中一些控制点的位移及插值方法来描述的空间变换)。
3.1 仿射变换(affine transformation)
其中 A 是变形矩阵,b是平移矢量。在2维空间,A可以按如下的四个步骤分解:尺度、伸缩、扭曲、旋转
(1)尺度
(2)伸缩
(3)扭曲
(4)旋转
即:
图2 人脸图象和掩膜图象
3.2 透视变换(Perspective Transformation)
透视变换是中心投影的射影变换,在用非齐次射影坐标表达时是平面的分式线性变换,具有如下的形式:
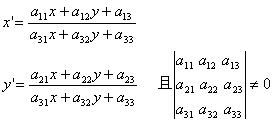 |
(参见:丘维生,解析几何,北京大学出版社,1996。)
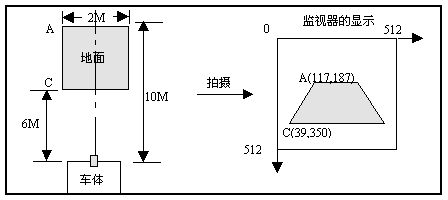
透视变换常用于图象的校正,例如在移动机器人视觉导航研究中,由于摄象机与地面之间有一倾斜角,而不是直接垂直朝下(正投影),有时希望将图象校正成正投影的形式,就需要利用透视变换。
![]() 重投影变换的应用实例(透视变形的校正)
重投影变换的应用实例(透视变形的校正)
(根据孙健同学的硕士论文摘录改编,祥见:孙健,面向室外移动机器人THMR-III导航的路标识别算法的研究,硕士学位论文,清华大学计算机系,1997.5)
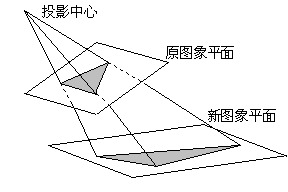
如果将摄取到的图象映射到平行于地面的平面上,其效果相当于摄影机把姿态改变为垂直于地面向下看,就会在这个新的平面上得到物体真实形状。由于这种映射相当于将原图象重新投影到另一个成象面上,故称之为重投影变换,并将映射后得到的图象称为重投影图象。
图3. 重投影示意图
在两个坐标平面之间的投影变换的数学形式如下:
设(x, y)是坐标平面XOY中的一点,(x’,y’)是(x,y)在坐标平面X’OY’中对应的象点,则有
其中a,b,c,d,e,f,u,v都是常量。
确定两个平面之间的投影变换只需要在两个平面上找到四对“物点和象点”,有这四对点的对应关系就可以确定a,b,c,d,e,f,u,v。具体而言,用一个规范化坐标系(平面)作为重投影平面,首先建立从规范化坐标(NormalCoordinate)到原始图象坐标(Oringinal Coordinate)的变换,其形式为
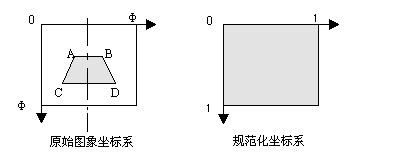
在地面上取定一个矩形(不一定是正方形),要求它的边平行或垂直于车体轴线,这样的矩形在原始图象中显示为一个等腰梯形,如图4.所示。
图4. 规范化坐标系和原始图象坐标系
设A点的坐标为(x1,y1),C点坐标为(x2,y2),则B、D的坐标分别是(φ-x1,y1)和(φ-x2,y2)。经过投影,ABCD四个点依此与规范化坐标系中的(0,0),(1,0),(0,1),(1,1)四个点相对应。把此对应关系代入上式,得
可以求得如下的各待定常数:
以上变换的逆变换OrgToNormal的形式是
把四对点的对应关系代入上式,得到待定系数的计算方法为:
公式中只需确定(x1,y1)和(x2,y2),确定这几个参数的方法如图5.所示:
图5. 几何关系参数示意图
(注:“重投影变换”源于:朱志刚,林学闫,“重投影变换在智能移动机器人视觉系统的应用”,模式识别与人工智能,1990,Vol.5,No.2)
4.几何校正
几何校正通过由已知的控制点(栅格)建立起来的几何变换(.\download_IPCVPR\GeometricsTransformation\GeometricTransformations.htm)进行。
左图:走廊的原图象;中图:透视变换将图象中的地砖校正成正方形;右图:透视变换将门的四角(原图最右侧的门,有把手的门)校正成矩形。(图片来源:Andrew Zisserman,Robotics Research Group, University ofOxford, http://www.dai.ed.ac.uk/CVonline/LOCAL_COPIES/EPSRC_SSAZ/node10.html)
5.图象卷绕(Image Warping)
图象卷绕是通过指定一系列控制点的位移来定义空间变换的图象变形处理。非控制点的位移根据控制点进行插值来确定。有时利用多项式函数来拟合控制点之间的对应关系,这时称为多项式卷绕(Polynomial Warping)。一般情况下,由控制点将图象分成许多多变形区域,对每个变形区域使用双线性插值函数来填充非控制点。
6.图象变形(Image Morphing)
变形是使图象中的一个物体逐渐变形为另外一个物体的过程。从一起始图象出发,利用渐隐(dissolve)技术,使起始图象逐渐“淡出(fadeout)”,而目标图象则逐渐“淡入(fade in)”,同时以对应物体为转换控制对象,通过选择控制点及控制线来建立插值过程,让物体上的点从它们的起始位置逐渐移向对应的终止位置。
演示播放(..\Demos\chapter06\morph\ahzmorph.avi)
作业
- 使用UleadMorph应用,选择控制点或控制线及网格,观察图象变形,说明原因。
- 编制实现透视及仿射变换的程序,通过交互输入参数观察效果。
- 有两幅人像摄影照片(例如,一幅是明星的剧照,另一幅是你自己的照片),试设计一个程序,通过少量的交互选择若干重要的控制点,通过图象卷绕将其中一幅照片中的人脸部分用另一个人的脸部替换
返回主目录 返回本章目录
清华大学计算机系 艾海舟
最近修改时间:2001年7月18日
出处:http://media.cs.tsinghua.edu.cn/~ahz/digitalimageprocess/CourseImageProcess.html