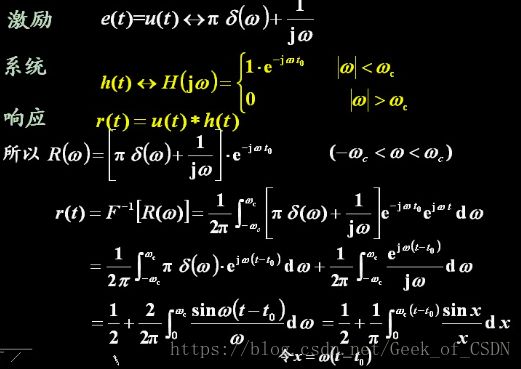信号与系统公式笔记（7）
主要关于第四章 连续时间系统频域分析（继续讲傅里叶变换的应用）
学习建议：教材看1~2遍，例题做1遍，注意积累
重点内容：
1. 傅里叶变换形式的系统函数
2. 调制和解调
主要内容：
1.傅里叶变换模与相位
2.LTI系统的幅频特性与相频特性，系统的失真
3.线性系统的信号失真
4.理想低通滤波器
5.调制与解调
在时域，系统特性由 h(t) h ( t ) 描述， h(t) h ( t ) 就是系统的冲激响应；
在频域，系统特性由 H(jω H ( j ω 描述（ H(jω H ( j ω 就是 h(t) h ( t ) 的傅里叶变换结果）
傅里叶变换的模和相位表示
无论CTFT还是DTFT，一般情况下都表现为一个复函数。
（就是模和相位的形式）
这表明一个信号携带的所有信息分别包含在其频谱的模和相位中。
LTI系统频率响应的模和相位表示
LTI系统对输入信号所起到的作用包括两个方面：
1.改变输入信号各频率分量的幅度
2.改变输入信号各频率分量的相对相位
记得在频域相乘就是在时域卷积的说。
上面这个可以结合模电知识理解。
傅里叶变换形式的系统函数
H(jω)=R(jω)E(jω) H ( j ω ) = R ( j ω ) E ( j ω ) 就是系统频响（这是系统函数里面的一种特殊情况，更深入的会在第五章学到）。重要的是PPT里面下半部分出现的公式，这个经常用来求特定输入下LTI系统的输出，就是频域的乘积相当于时域的卷积。
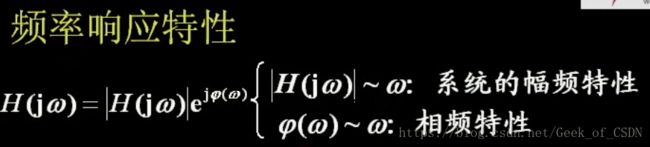
上面只是定义。通常就是用来画图的。
注意结果里面出现的 ejω0t e j ω 0 t ，这个刚好是输入信号。这是个性质：当输入刚好是 e(t) e ( t ) 的时候，输出就是输入与系统频响的乘积。（ e(t) e ( t ) 就是特征函数，第八章会更深入的讲）。
补充：为什么用冲激信号算出冲激响应就可以求出不同输入信号输入后对应的系统输出。
因为冲激信号 δ(t) δ ( t ) 对应的频谱是 1 1 ，所以可以算出这个系统对不同频率的信号的响应能力。
系统函数的物理意义
系统可以看作是一个信号处理器
激励： E(jω) E ( j ω )
响应（ R(jω) R ( j ω ) ）= H(jω)⋅E(jω) H ( j ω ) ⋅ E ( j ω ) （对信号各频率分量进行加权，联想卷积）
对于不同的频率 ω ω ，有不同的加权作用，这也是信号分解，求响应再叠加的过程。
例题
要注意记住正弦信号对应的频谱（就是被挡住的那部分，记住就是了）。
下面出现的频移特性是由 1→2πδ(ω) 1 → 2 π δ ( ω ) 和频移特性得出的（反变换）。
注意上面里面的 ejφ(ω) e j φ ( ω ) 里面的 jφ(ω) j φ ( ω ) 是奇函数（用的是 arctan a r c t a n 计算出来的， φ(ω)=−arctanω φ ( ω ) = − a r c t a n ω ），然后记得 δ(t0)⋅x(t)=x(t0) δ ( t 0 ) ⋅ x ( t ) = x ( t 0 ) ，所以可以得到上面用黄色点亮的式子。
最后得出
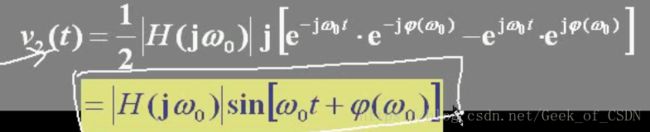
这个结论很重要，因为输入和输出是同频率的，只是幅度有加权和相位有平移（据说常考）。
不懂的话看这个例题
上面这类问题一定要会算。
线性系统对激励信号的响应
只是个例题，关键在思路里面的： R(jω) R ( j ω ) ）= H(jω)⋅E(jω) H ( j ω ) ⋅ E ( j ω )
注意：上面的门信号其实就是平移之后的矩形脉冲信号。
所以可以得到
EτSa(ωτ2) E τ S a ( ω τ 2 )
最后求反变换（难在这里）
说明
线性系统的信号失真
意思是：波形在幅度和时移上变化了不会让波形失真。这是不失真成立的条件。
傅里叶变换之后的频谱要符合上面这个特性（其实是直接把最上面的公式傅里叶变换了，这里频域对应着系统在时域的平移）
上面两张图片右边的公式都是离散情况下成立的公式。
注意公式里面的 － － ，群延时其实就是一组信号在通过系统时候产生的延时。
这里只需要了解（拓展内容）
群延时的概念，了解就可以。。。
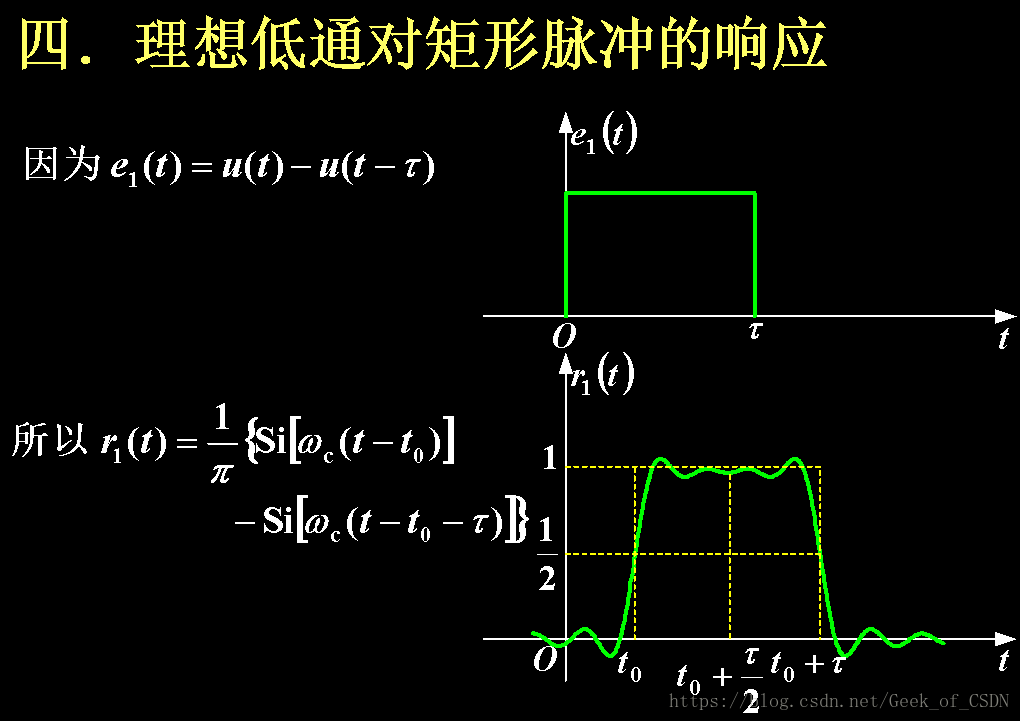
理想低通滤波器
一、理想低通滤波器的频率特性
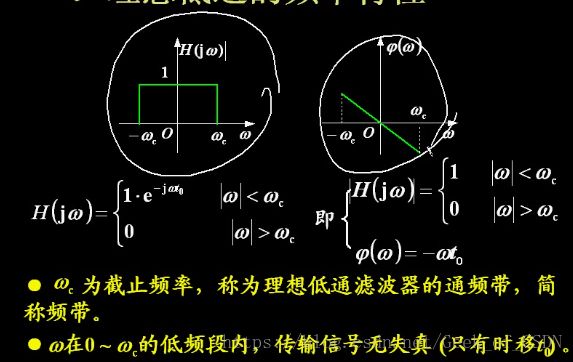
左边是幅频特性，右边是相频特性。右边的相频特性保证了通关过系统的信号不失真（所以过原点）。
下面大括号里面的那些只是对上面两个图的数学描述。
对应的冲激响应：
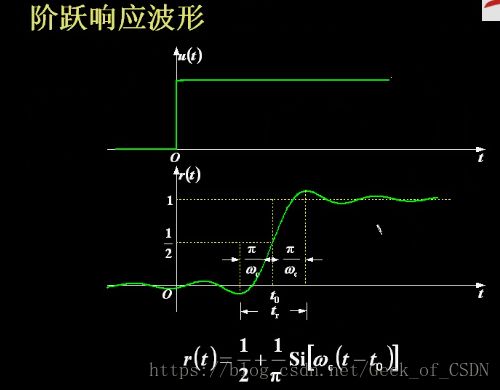
对应的波形
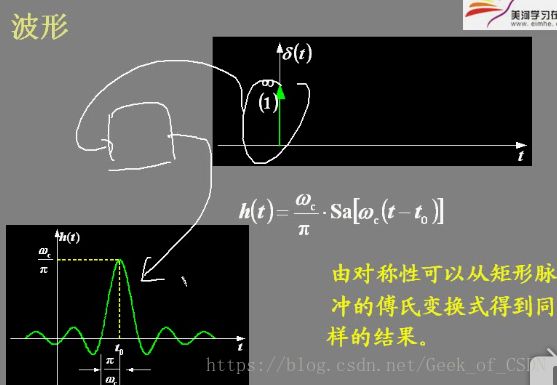
非因果系统原因：从 h(t) h ( t ) 看， t<0 t < 0 时已有值。（只要 t<0 t < 0 有值就是非因果系统，因为输出信号在 t=0 t = 0 输入信号出现前就已经出现，所以是非因果的）
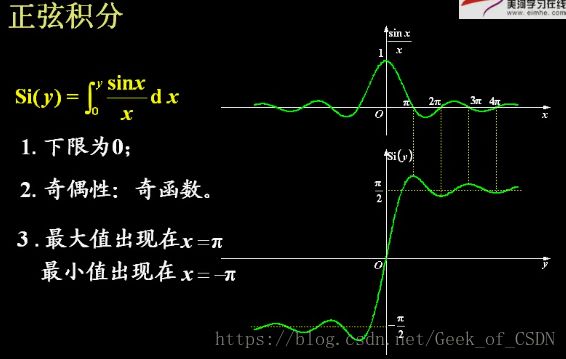
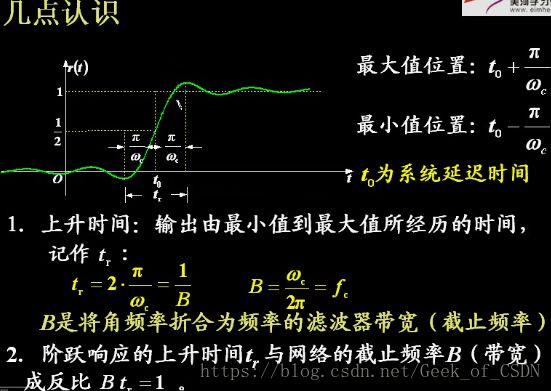
理想低通的阶跃响应（不是重点）
然后对应的图形
了解一下就可以了。。。不是重点。
理想低通对矩形脉冲的响应
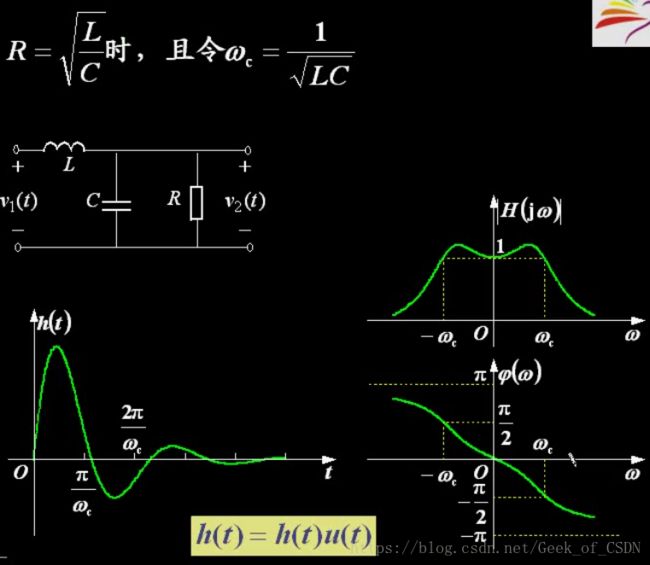
一种可实现的低通滤波器
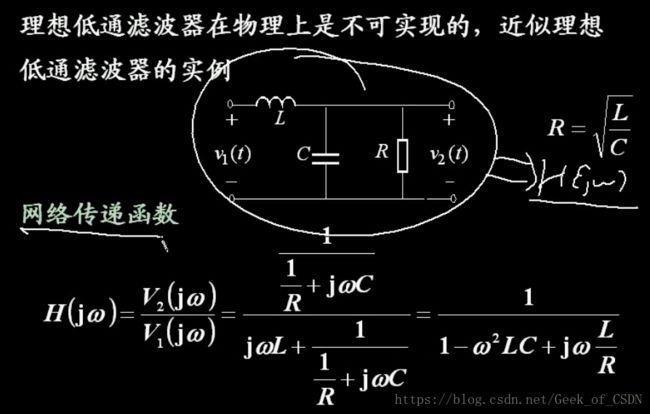
上面的公式里面用到了分压的定理（KVL）
只是个例子。。。
调制与解调
傅里叶变换的应用中最重要的一个（取样也很重要，都要掌握）。
调制定义：用一个信号去控制另一个信号的某一个参量的过程。
被控制的信号是载波。
控制信号被称为调制信号,也成为基带信号。
调制
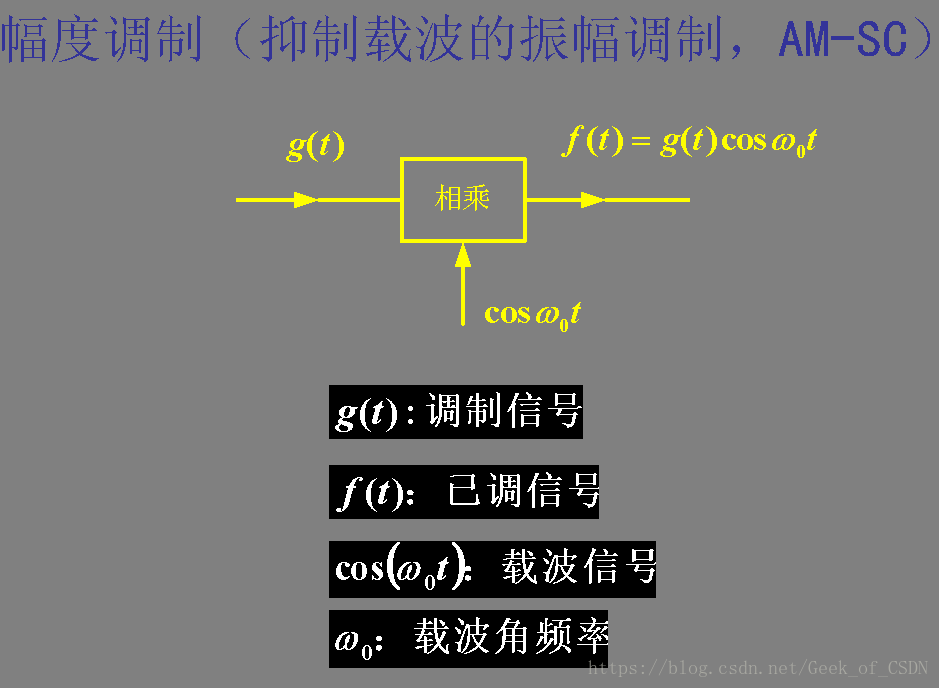
调制其实就是直接把调制信号和载波信号相乘（相当于在频域上做卷积）。
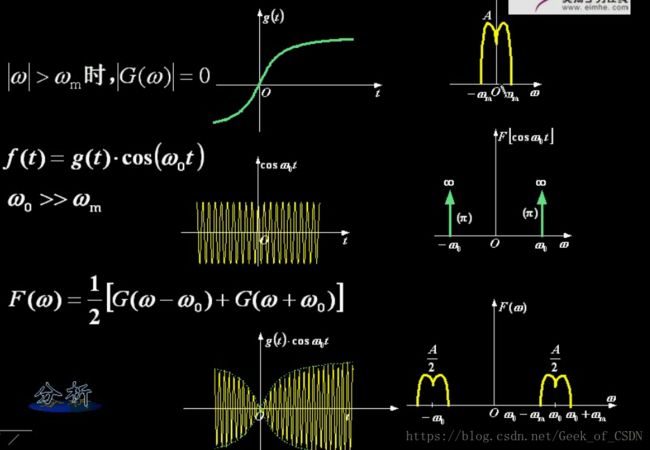
注意余弦信号对应的频谱（ π[σ(ω−ω0)+σ(ω+ω0)] π [ σ ( ω − ω 0 ) + σ ( ω + ω 0 ) ] ）。
这样也就实现了信号从低频到高频的搬运。
下面这个是直接用频移性质实现的：
上图里面最下面的公式是数学推导。
（实际情况中会让 ω0>>ωM ω 0 >> ω M ）
解调
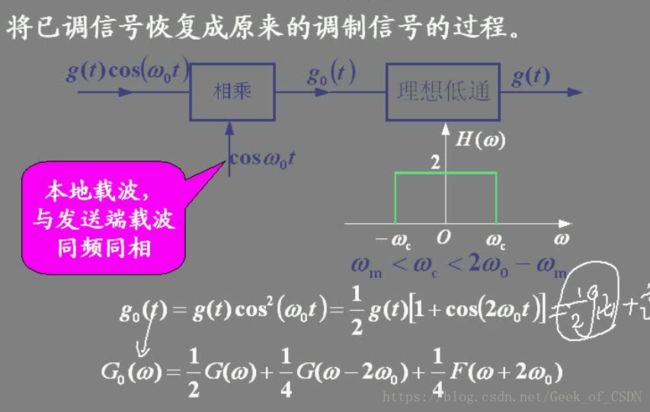
其实关键在下面这个图：
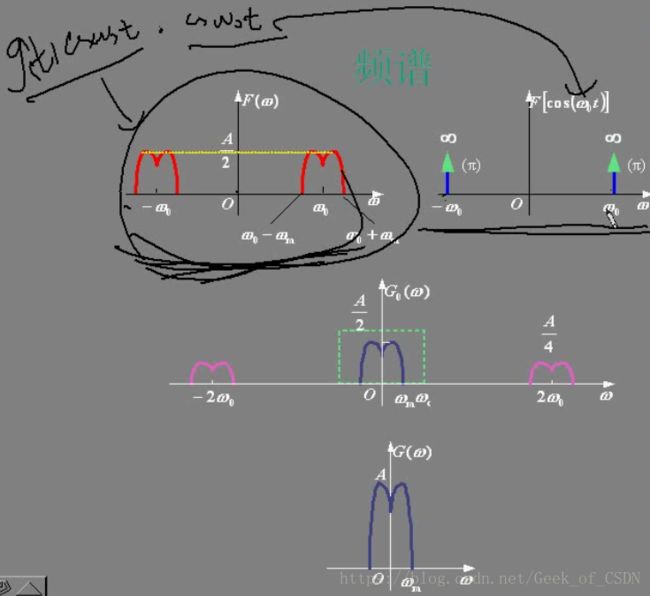
因为 −ω0 − ω 0 里面的和 ω0 ω 0 做卷积，所以向右移动，回到原点，右边那个差不多。
最后的出来的信号变成中间那个图（注意幅度是 A2 A 2 ），然后这时候用低通滤波器就可以把信号给取出来。
其实上面图里面中间的图对应的是最上面的图的公式：
载波相位的影响：
这种情况主要是对应实际应用时出现的调制和解调用的波形相位不一致的情况。。。
