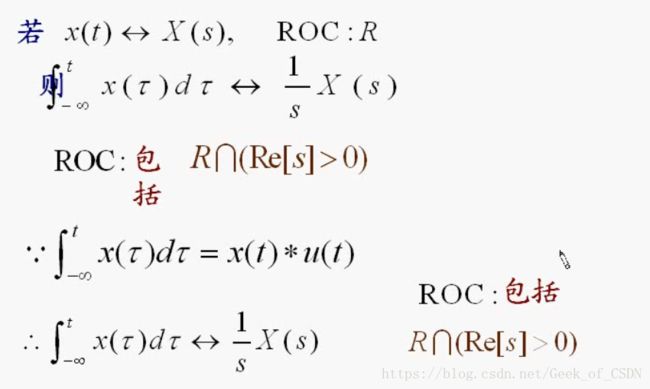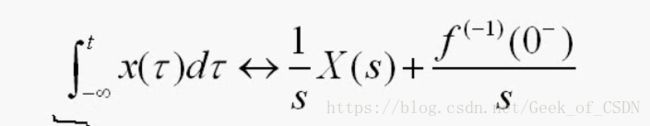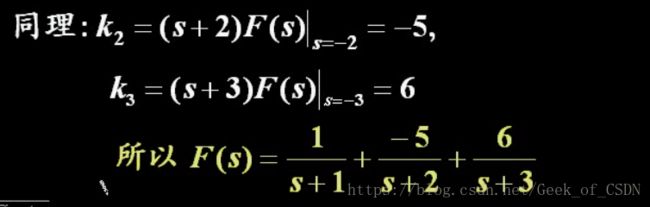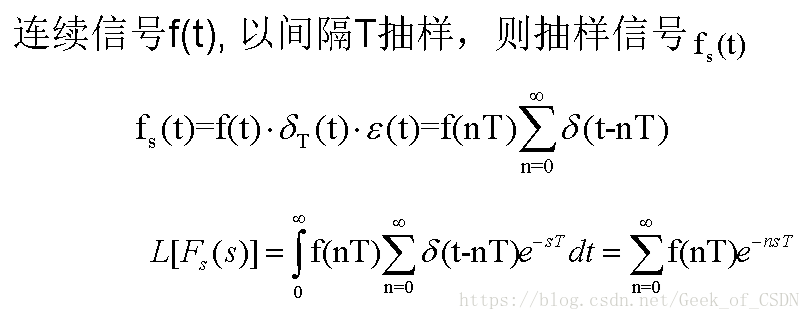信号与系统公式笔记（8）——拉普拉斯变换

这里是关于第5章的内容，拉普拉斯变换。。。其实基本上内容和傅里叶变换差不太多，基本上傅里叶变换学到的概念都可以在修改后用在拉普拉斯变换上。大部分截图来自齐开悦博士的课程录像的说。

傅里叶变换是拉普拉斯变换的特殊情况，拉普拉斯是傅里叶变换的推广，它们之间的最大不同就是拉普拉斯实在 s=σ+jω s = σ + j ω ，积分域不同。

基本内容：
1. 拉普拉斯变换定义，收敛域
2. 拉普拉斯变换的性质（和傅里叶变换类似）（重要，能简化计算）
3. 拉普拉斯反变换（主要是部分分式法）
4. 拉普拉斯变换与电路分析（一定要记住元件对应的拉氏变换模型）
5. 系统函数（挺重要的性质，求出了系统函数可以很方便地求输出）
6. 拉普拉斯变换与傅里叶变换关系（关键词：虚轴）

---

对不符合狄利克雷条件的函数无法做傅里叶变换，所以搞出来个拉普拉斯变换。

用 eSt e S t 的例子： S=δ+jωeSt=eδt⋅ejωt S = δ + j ω e S t = e δ t ⋅ e j ω t

拉氏变换和Z变换时傅里叶变换的推广，傅里叶变换是它们的特例。

拉氏变换

拉氏变换定义与收敛域

---

从傅里叶变换到拉氏变换

双边拉氏变换定义：

最下面那个公式里面的积分极限的下限的 0− 0 − 是为了表示包括冲激信号（单边拉氏变换才有用）。

例如原信号是 e2t e 2 t ，让 δ=−3 δ = − 3 ，最后的积分对象就变成了\mathrm[e}^{-t} \mathrm[e}^{-t} ，这样在总体上就是收敛的，就可以用到傅里叶变换。这样拉氏变换就可以比傅里叶变换用得更广泛。

补充：如果一个信号是因果信号，那么单边拉氏变换和双边是一样的。

记得 u(t)→πδ(ω)+1jω u ( t ) → π δ ( ω ) + 1 j ω ，最后结果是 1S 1 S ，因为刚好 S>0 S > 0 ，不包含 0 0 ，所以没有冲激函数那部分。

拉氏收敛域在解题的时候必须要写出来。

ROC及零极点图例子：

具体的零极点图在上面的例题里面最下面的图已经有了。

ROC性质

时限信号因为一定可以做傅里叶分析，所以ROC是整个S平面。
第4条性质的证明：

第6条其实就是4、5的结合，因为双边可以分成左边和右边。

如果两个域没有公共部分，那么拉氏变换不存在。

结合例题看比较容易理解地说：

---

常用拉氏变换

上面要补充定义域：
1. Re(s)>0 R e ( s ) > 0
2. Re(s)>−a R e ( s ) > − a
3. Re(s)>0 R e ( s ) > 0
后面两个可以不用写因为是整个复平面上成立的。
上面的东东要直接当公式用

补充：

−e−atu(−t)→1s+aRe(s)<−a − e − a t u ( − t ) → 1 s + a R e ( s ) < − a

要分清楚，注意定义域不同（虽然变换结果相同的说）
上面图里面最后一条公式和拉氏变换的时移性质有关。
话说贫僧在理解拉氏变换的时候会想象成用无穷多个 σ σ 去和原信号在时域卷积（卷积就相当于在整个时域进行遍历/信号强度相乘/取样）因为卷积在复频域对应的就是信号的拉氏变换后的结果的乘积，而 σ σ 本身就是的拉氏变换结果就是1。所以可以把拉氏变换理解成用 σ σ 信号遍历/采样（所以积分区间是无穷）原信号的过程。
这样理解的话就可以用上面图厘米那的最后一条公式来理解拉氏变换的时移性质了。

部分公式有对应的证明过程，ppt上面有，看看就行。

---

拉氏变换的性质

最重要的其实是时域卷积对应频域相乘，这条性质在各个变换里面通用而且贫僧觉得是信号与系统的重要工具。

线性

其实线性也体现了齐次性和可加性（齐次性体现在 a1x1(t)=a1(y1(t) a 1 x 1 ( t ) = a 1 ( y 1 ( t ) ，可加性。。。就是可加性）。
还是一样的要注意收敛域（新信号的收敛域可能会变大，因为信号合成的时候可能会把他们的极点抵消掉）。
证明的话直接用拉氏变换的积分定义去证明。

收敛域变大的例子：

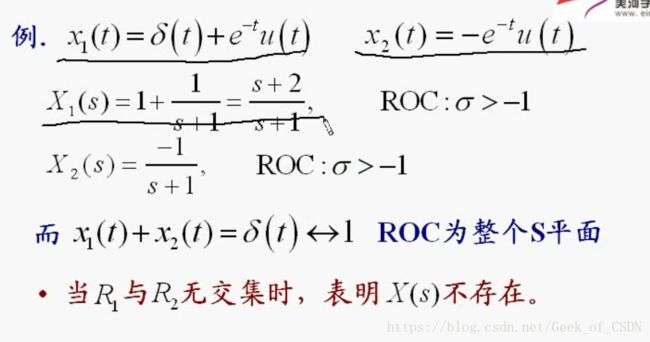
上面图里面的红色结论其实和例题无关。。。无视吧。。。

时移

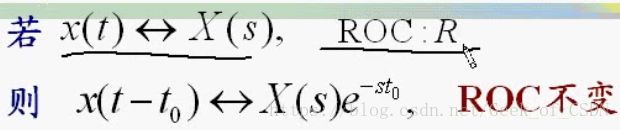
注意上面的收敛域不变。
用拉氏变换的积分定义也可以证明，不过贫僧更加喜欢把这个性质和 σ σ 的时移公式联系起来记忆。
话说傅里叶变换的时移性质是： x(t)→X(jω)x(t−t0)→X(jω)e−jωt0 x ( t ) → X ( j ω ) x ( t − t 0 ) → X ( j ω ) e − j ω t 0 ，傅里叶变换里面时移对应了频域的相位变换，拉氏变换里面除了相位变化之外还有镜像的幅度拉伸（ e−st=e−σte−jω e − s t = e − σ t e − j ω ）

s域平移

注意收敛域的变化。
时域有镜像的压缩/相位变换（旋转）对应了s域平移。
其实就是一个域里面产生了平移，那么在另一个域里面就会有对应的压缩/旋转。
一个例题：

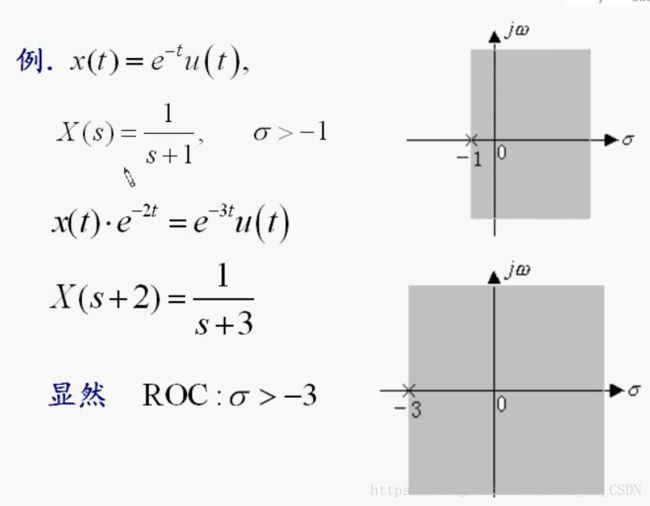
时域尺度变换

注意收敛域也缩放了。

信号变化在两个域上产生的影响和 Bfτ=1 B f τ = 1 的关系差不多，都是一个扩大一个减少（其实贫僧觉得也和测不准定理有关）。

这个是结论，要记住（结合下面的共轭对称性记）。

共轭对称性

证明也还是要用回拉氏变换的积分定义。

时域卷积性质（最重要的性质）

对解微分方程和避开卷积运算很有用。
还有对称的性质：
在频域卷积对应在时域乘积。

微分性质

则后面有两个公式，如果是双边信号那么上面的公式成立，如果是单边信号的话就是下面那个公式成立。（注意收敛域可能扩大，例如拉氏变换后的信号里面分母有s，刚好乘上s把分母的s抵消掉，那么就会扩大收敛域）
单边拉氏变换是从 0− 0 − 开始积分的， ∫+∞0− ∫ 0 − + ∞ ，所以公式是这个样子，双边是 −∞ − ∞ ~ +∞ + ∞ ，所以不用减东西。
高阶的看教材（注意二阶的单边的，要特别记住）。

S域微分

时域积分

上面那个是单边的信号。
单边的：

初值和终值定理

话说这个定理在傅里叶变换里面没有。

证明：


了解一下就可以了（不常用）。


贫僧觉得这个定理可以和积分定理联系起来记忆（记住结论就行了）。

上面这些通常用在简化计算上的说。

---

拉氏反变换

其实和傅里叶反变换差不多，只是换了个积分域所以公式有点变化。
下面是部分分式展开法（没有用留数定理的围线积分法、数值计算法）。

部分分式展开法

反变换过程（这里默认 F(s) F ( s ) 是真分式，如果不是就要先化成真分式和多项式的和）：
1. 找出 F(s) F ( s ) 的极点（分母因式分解）
2. 将 F(s) F ( s ) 展成部分分式
3. 查表求 f(t) f ( t ) （最后还是查表方便啊。。。）

k1…kn k 1 … k n 之类的是后面用公式确定的，怎么确定的话看下面例题就知道了。

还有另外一种情况，极点是共轭复数，但是步骤是一样的。

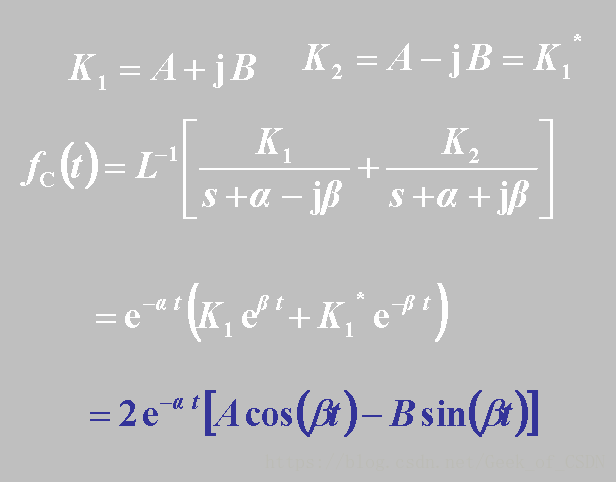
最后那个结果不用纠结，大概知道原理就行了（实在是纠结的话自己动笔算。。。还是欧拉和三角函数的特性）。

例题：

还有一种情况：有重根存在

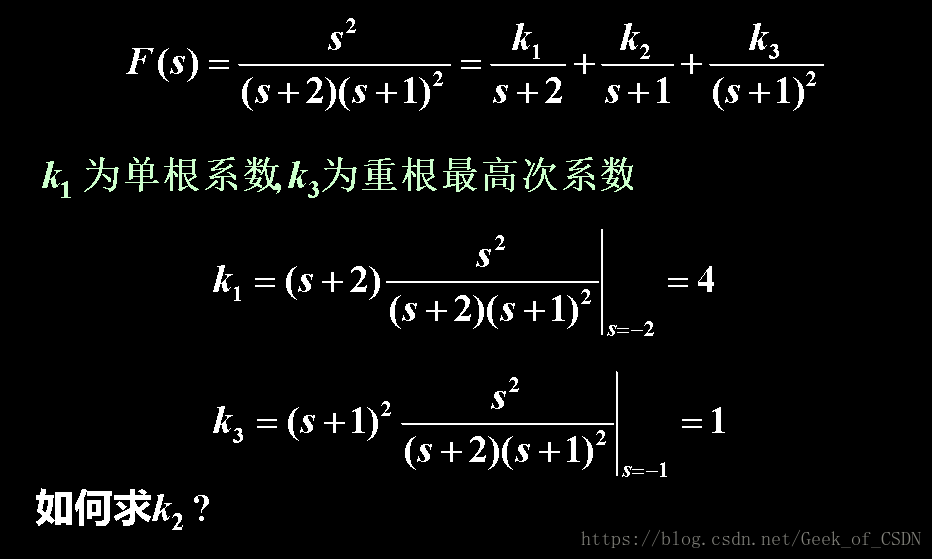
求重根的时候就多一个求导的步骤，其他的还是差不多。

结果：

其实还可以直接拆解，并保证左右两边相等，那么就可以避免求导求系数。

另外两种情况

1. 非真分式（假分式），这种情况直接化成分式和多项式再直接逆变换就可以了（用多项式除法）
2. 含 e−s e − s 的非有理式（另外再分两种情况，一种是非有理式在分子里面出现，另外一种以 (1+e−s) ( 1 + e − s ) 或 (1−e−s) ( 1 − e − s ) 形式出现在了分母里面）

下面主要是关于第二种情况：

e−s e − s 不参与部分分式运算

这时就直接用时移性质来解就可以了。

插播时移的例题：

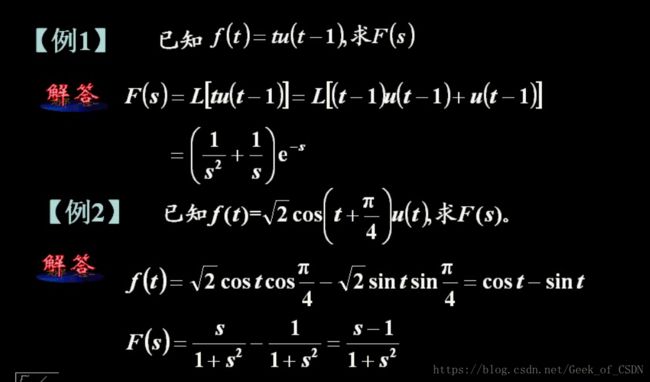
注意；例一要加上定义域（>0），例二最好能够根据记住了的公式直接写出答案。

用拉氏变换分析电路、s域原件模型

主要内容：
1. 用拉氏变换分析电路的步骤
2. 微分方程的拉氏变换
3. 利用元件的s域模型分析电路

分析电路的步骤

1. 列s域方程（从两方面入手）
   a. 列时域微分方程，用微积分性质求拉氏变换
   b. 直接按电路的s域模型建立代数方程
2. 求解s域方程
3. F(s)→f(t) F ( s ) → f ( t ) ，得到时域解答

电路元件的s域模型：

例题：

周期信号与抽样信号的拉氏变换

11−e−sT 1 1 − e − s T 是个无穷多项等比级数，所以写成这个形式。
具体的看教材，这里记住公式。
如果分母是 1+e−sT 1 + e − s T ，那么就要变成 F(s)=F1(s)11+e−sT=F1(s)1−e−sT1−e−2sT F ( s ) = F 1 ( s ) 1 1 + e − s T = F 1 ( s ) 1 − e − s T 1 − e − 2 s T ，周期变成2T了。

注意积分对象是t，和T无关。

系统函数

定义：用 h(t) h ( t ) 表示线性时不变离散系统的冲激响应，这时给一个输入 x(t) x ( t ) 系统输出就是 y(t)=x(t)∗h(t) y ( t ) = x ( t ) ∗ h ( t ) ，对应频域 Y(s)=X(s)H(s) Y ( s ) = X ( s ) H ( s ) 。 H(s)=Y(s)X(s) H ( s ) = Y ( s ) X ( s ) 定义为系统函数。
系统函数主要方便在直接用输入拉氏变换后的结果乘以系统函数，再拿乘之后的结果拉氏反变换就可以得到系统的输出。
还是很容易的概念，平时做一下题目就知道怎么用了。

拉氏变换和傅里叶变换的联系

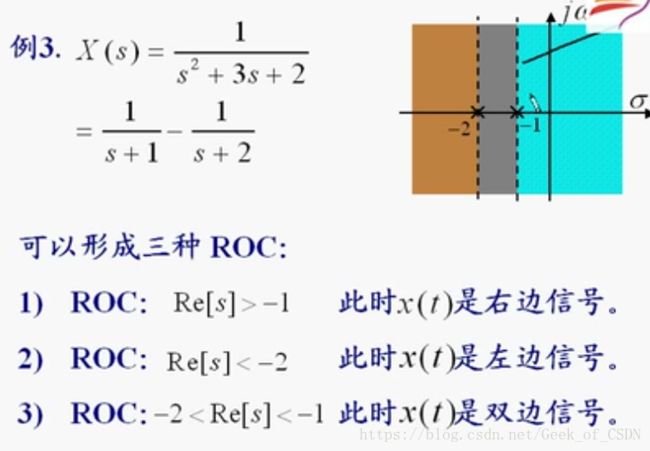
第一种情况因为不包含虚轴（ jω j ω ）所以傅里叶变换不存在，后面的情况类似，主要和虚轴有关。拉氏变换就是傅里叶变换的推广，傅里叶变换是在虚轴上的拉氏变换。
上面的情况对右边信号才成立，左边信号的话要另外考虑（其实还是看定义域有没有包含虚轴）。
第三种情况的例子： u(t) u ( t ) 在拉普拉斯变换里面对应 1s 1 s ，但是傅里叶变换里面对应 πσ(ω)+1jω π σ ( ω ) + 1 j ω 。