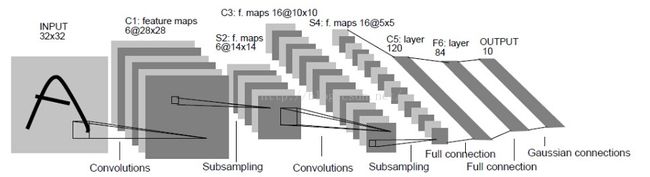
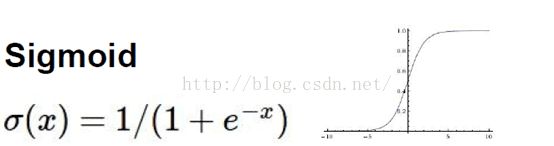神经网络之LeNet结构分析及参数详解
LeNet一共有7层(不包括输入层)
输入层:
输入图像的大小为32*32,这要比mnist数据库中的最大字母(28*28)还大。
作用: 图像较大,这样做的目的是希望潜在的明显特征,比如笔画断续,角点等能够出现在最高层特征监测子感受野的中心。
其他层:
C1,C3,C5为卷积层,S2,S4为降采样层,F6为全连接层,还有一个输出层。
每一个层都有多个Feature Map(每个Feature Map中含有多个神经元),
输入通过一种过滤器作用,提取输入的一种特征,得到一个不同的Feature Map。如下图所示:


各层详解:
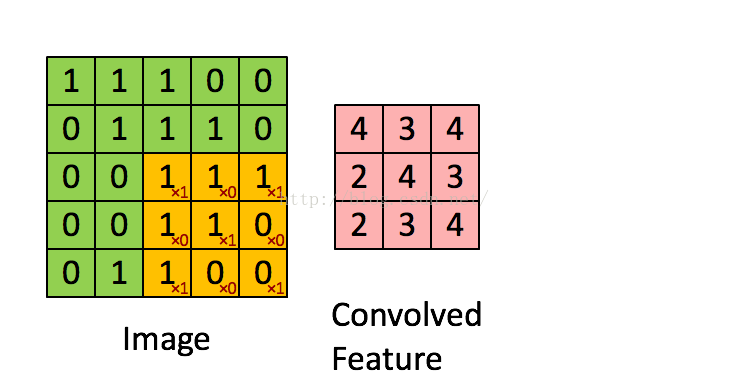
卷积运算的优点:通过卷积运算,可以使原信号特征增强,并且降低噪声。
卷积对于二维图像中的效果就是:对于图像中的每个像素邻域求加权和得到该像素点的输出值。
1. C1卷积层
C1 是一个卷积层,由6个Feature Map组成。 每一个Feature Map中的每个神经元与输入中5*5的区域相连(也就是Filter的大小),Feature Map的大小为28*28,
C1一共有156个参数,因为5*5个参数加上一个bias,一共又有6个Filter,所以为:(5*5+1)*6=156,一共有156*(28*28) = 122304个连接。
2. S2 下采样层(Pooling)
下采样的作用: 利用图像的局部相关性原理,对图像进行子抽样,可以减少数据处理量,同时又保留有用的信息。
同样的,有6*14*14, 6个Feature Map。
池化层一般有两种方式:
(1) Max_Pooling: 选择Pooling窗口中最大值最为采样值
(2) Mean_Pooling: 将Pooling窗口中的所有值相加取平均,然后以平均值最为采样值。

说明:
每个单元的2*2的感受野()并不重叠,因此S2中每一个Feature Map的大小为C1中Feature Map中大小的1/4。行列各位1/2。所以,S2有12个可训练的参数和5880个连接。个人感觉,5880是这么来的,Filter的大小为:2*2,一个偏差bias,6个Feature Map,则可训练参数个数为:(2*2+1)*6 = 30,连接数为:30*(14*14)= 5880
12 则为: 6个2*2的小方块,加上一个bias,为(1+1)*6=12
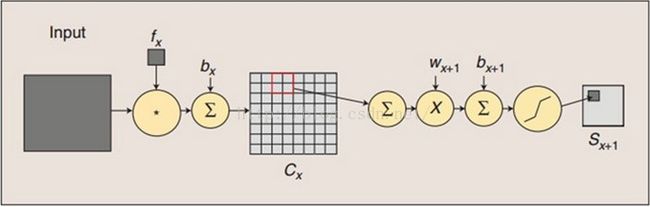
上图说明了卷积过程子采样过程。卷积过程中,用一个可训练的过滤器f
x
去卷积一个输入图像,然后添加一个偏置bx
,得到卷积层Cx 。子采样过程就是:每个邻域4个像素变为一个像素,然后加上标量Wx 加权,最后再增加偏置bx+1 ,接着通过一个sigmoid激活函数,产生一个大概缩小了4倍的特征映射图Sx+1。
3. C3层 卷积层
同样的,Filter大小认为5*5,去卷积S2,得到的Feature Map为10*10大小。每一个Feature Map中包含10*10个神经元。C3层有16个不同的Filter,所以会得到16个不同的Feature Map。
C3中的每一个Feature Map连接到S2的所有6个Feature Map或者是几个Feature Map。表示本层的Feature Map是上一层提取的Feature Map的不同组合。为什么不把S2的每一个Feature Map连接到S3的每一个Feature Map中?原因有2: 第一,不完全连接机制连接的数量保持在合理范围,第二,这样破坏了网络的对称性,由于不同的Feature Map有不同的输入,所以迫使他们抽取不同的特征(理想状态特征互补)。
如果:C3的前6个Feature Map以S2中的3个相邻的Feature Map子集为输入,接下来的6个Feature Map以S2中相邻的4个Feature Map作为输入,接下来的3个以不相邻的4个Feature Map子集作为输入,最后一个将S2中所有的Feature Map作为输入的话,C3将会有1516个可训练参数和151600个连接。
因为6*(3*25+1) + 6*(4*25+1) + 3*(4*25+1) + 1(6*25+1) = 1516。
连接数为:1516*10*10=151600。
4. S4层 Pooling层
由16个5*5的Feature Map组成,Feature Map中每个单元与C3中相应的Feature Map的2*2邻域相连。
S4有32个可训练的参数和2000个连接
同S2,(1+1)*16=32. 连接数为: (2*2+1) * 16 * 5*5 = 2000
5. C5 卷积层
这一层有120个Feature Map,每个单元与S4层的全部的16个5*5的邻域相连。 S4的Feature Map的大小也是5*5,这一层的Filter大小也是5*5,所以,C5的Feature Map的大小为1*1。
此时构成了S4与C5之间的全连接。但这里C5表示为卷积层而不是全连接层,是因为如果LeNet的输入变大,而其他保持不变,此时的Feature Map的大小就比1*1要大。
C5有48120个可训练的链接: (5*5*16 +1) *120 = 48120。
6. F6 全连接层
有84个单元(之所以是84是因为输入层的设计),F6计算输入向量和权重向量之间的点积,再加上一个偏置,最后将其传递给sigmoid函数产生一个单元i的一个状态。
一共有10164个可训练的连接,为:84*(120+1)=10164。
7. 输出层
输出层由欧式径向基函数(Euclidean Radial Basis Function)单元组成,每类一个单元,每个单元有84个输入。
也就是说: 每个输入RBF单元计算输入向量和参数向量之间的欧氏距离。输入离参数向量越远,RBF输出越大。一个RBF输出可以理解为衡量输入模式和RBF相关联的一个模型的匹配程度的惩罚项。给定一个输入模式,损失函数应该能使F6的配置和RBF参数向量(模式的期望分类)足够接近。
每一个单元的参数是人工选取并保持固定的。这些参数向量的成分被设计成-1或1。虽然这些参数可以以-1或1等概论方式任取,或者是构成一个纠错码,但是被设计成一个相应字符类的7*12的格式化图片。

RBF参数向量骑着F6层目标向量的角色。需要指出这些向量的成为为+1或者-1,正好在F6 Sigmoid函数的范围内,因此可以防止sigmoid函数饱和。+1和-1是sigmoid函数的最大弯曲点,这也使得F6单元运行在最大非线性范围内。
必须避免sigmoid函数饱和,否则会导致损失函数较慢收敛和病态问题。
卷积神经网络在本质上是一种输入到输出的映射,它能够学习大量的输入与输出之间的映射关系,而不需要任何输入与输出之间的精确的数学表达式,只要用已知的模式对卷积神经网络加以训练,网络就具有输入与输出之间的映射能力。卷积网络是有监督学习,所以它的样本集都形如:(输入向量,理想输出向量)之类的向量对构成。
在训练之前,所有权值都用一些不同的小随机数进行初始化,小的随机数可以保证网络不会因权值太大而进入饱和状态,从而导致训练失败。不同则保证网络可以正常学习。
如果要是用相同的数去初始化矩阵,网络会没有学习的能力。
网络的训练过程为:
分为四步:
(1) 在一批数据中取样(Sample a batch of data)
(2)前向过程计算得到损失(Forward prop it through the graph, get loss)
(3)反向传播计算梯度(Backprop to calculate the gradient)
(4)利用梯度进行梯度的更新(Updata the parameters using the gradient)
这里,网络的训练主要分为2个大的阶段:
第一阶段,向前传播阶段:
1)从样本集中取一个样本(X,Yp),将X输入网络;
2)计算相应的实际输出Op。
在此阶段,信息从输入层经过逐级的变换,传送到输出层。这个过程也是网络在完成训练后正常运行时执行的过程。在此过程中,网络执行的是计算(实际上就是输入与每层的权值矩阵相点乘,得到最后的输出结果):
Op=Fn(…(F2(F1(XpW(1))W(2))…)W(n))
第二阶段,向后传播阶段
1)算实际输出Op与相应的理想输出Yp的差;
2)按极小化误差的方法反向传播调整权矩阵。
参考转载:
来源: http://blog.csdn.net/qiaofangjie/article/details/16826849http://blog.csdn.net/cyh_24/article/details/51440344