树回归问题

1. 树回归

基于之前的线性回归，树回归归根结底也是回归，但不同的是，树回归可以更好的处理多特征的非线性回归问题，其基本思想就是切分数据集，切分至易拟合的数据集后进行线性回归建模。（复杂数据的局部建模）

回归树
节点为数值型/标称型
模型树
节点为线性模型

2.优缺点

优点: 可以对复杂的非线性数据建模
缺点: 结果不易理解，抽象化

3.伪代码

'''
部分核心代码伪代码

1.建树creatTree伪代码:
找到最佳切分特征(值)
if 节点不能继续切分
    返回节点值
else
    切分数据集
    左右子树递归调用creatTree

2.最佳切分特征值函数chooseBestSplit伪代码

预剪枝1判断数据集是否为一个元素
设立最大值标记(又是打擂台)
计算初始误差
for 每个特征：
    for 每个特征值：
        切分数据集
        预剪枝2 数据量限制
        计算拆分后误差
        打擂台记录最小误差
预剪枝3 误差变动限制
拆分数据集
预剪枝4 数据量限制
返回最佳切分数据特征(值)

3.后剪枝prune函数伪代码

if 数据集空 合并子树
if 左/右有子树
    拆分数据集
if 左子树不是叶子
    递归调用prune函数
if 右子树不是叶子
    递归调用prune函数
if 都是叶子节点
    拆分数据集
    比较拆分误差 与 原始误差
    记录最优
返回tree

'''

3.1 其它函数列表

'''
modelTree
modelErr modelLeaf linerSolve modelTreeEval (计算误差 节点生成2 模型预测)

regTree
regErr regLeaf regTreeEval (同上)

prune
isTree getMean (判断是否节点 返回平均值)

详情见代码注释
'''

4.代码

# coding:utf-8

from numpy import *

# 加载数据集
def loadData(fileName):
    dataMat = []
    with open(fileName) as txtFile:
        for line in txtFile.readlines():
            dataMat.append(map(float, line.split()))
    return dataMat  # 200*2

# 线性回归 最小二乘法 modelTree也会用到
def linerSolve(data):
    m, n = shape(data)
    X = mat(ones((m, n)))
    Y = mat(ones((n, 1)))
    X[:, 1:n] = data[:, 0:n - 1]  # x从1取数据的前n-1列 第0列是常数1
    Y = data[:, -1]
    xtx = X.T * X  # xTx.I * XTy
    if linalg.det(xtx) == 0:
        print "error 0!"
        return
    ws = xtx.I * X.T * Y
    return ws, X, Y

# modelTree 误差 是平方加和
def modelErr(errData):
    ws, X, Y = linerSolve(errData)
    yPre = X * ws
    return sum(power(yPre - Y, 2))

# modelTree 不用数据 用ws生成叶节点的模型
def modelLeaf(data):
    ws, X, Y = linerSolve(data)
    return ws

# regTree 计算误差 var均方差*数量=总方差
def regErr(errData):
    return var(errData[:, -1]) * shape(errData)[0]

# regTree 返回叶子节点的值,用了均值 所以说 叶子节点是一个值
def regLeaf(data):
    return mean(data[:, -1])

# 根据特征与阀值 分成两份数据
def binSplitTree(data, feat, value):
    mat0 = data[nonzero(data[:, feat] > value)[0]]
    mat1 = data[nonzero(data[:, feat] <= value)[0]]
    return mat0, mat1

# 判断是否是树 (上面说到 叶子节点是数值)
def isTree(obj):
    return type(obj).__name__ == 'dict'

# 利用getMean获取节点均值 剪枝
def getMean(tree):
    # print tree
    if isTree(tree['Right']): tree['Right'] = getMean(tree['Right'])
    if isTree(tree['Left']): tree['Left'] = getMean(tree['Left'])
    return (tree['Left'] + tree['Right']) / 2.0

# 后剪枝:递归
def prune(tree, data):
    if shape(data)[0] == 0:  # 数据集空 合并子树
        return getMean(tree)
    # 左右有子树 进行剪枝
    if isTree(tree['Left']) or isTree(tree['Right']):
        lSet, rSet = binSplitTree(data, tree['Feat'], tree['Value'])
    if isTree(tree['Left']):
        tree['Left'] = prune(tree['Left'], lSet)
    if isTree(tree['Right']):
        tree['Right'] = prune(tree['Right'], rSet)
    # 都不是子树 那么就是叶子节点 讨论(不)合并的误差看 是否合并
    if not isTree(tree['Left']) and not isTree(tree['Right']):
        # print "not tree", tree
        lSet, rSet = binSplitTree(data, tree['Feat'], tree['Value'])
        errorNoMerge = sum(power(lSet[:, -1] - tree['Left'], 2)) + sum(power(rSet[:, -1] - tree['Right'], 2))  # 不合并误差
        treeMean = (tree['Left'] + tree['Right']) / 2.0  # 利用平均值计算合并误差
        errorMerge = sum(power(data[:, -1] - treeMean, 2))  # 合并误差
        # print errorMerge,errorNoMerge
        if errorMerge < errorNoMerge:  # 判断
            print "merging"
            return treeMean  # 合并
        else:
            return tree  # 不合并
    else:
        return tree  # 完成 返回‘根’

# 选择最佳分配方案
def chooseBestSplit(data, leafType, errType, ops=(1, 4)):
    if len(set(data[:, -1].T.tolist()[0])) == 1:  # 预剪枝 1:只有一个元素 set 判断重复
        # print "len is:", len(set(data[:, -1].T.tolist()[0]))
        return None, leafType(data)
    bestFeat = 0  # 最佳特征
    bestValue = 0  # 最佳特征值
    numLim = ops[1]  # 节点数目限制
    errorLim = ops[0]  # 误差限制
    errorFirst = errType(data)  # 开始时的误差
    bestError = inf  # 最佳误差
    m, n = shape(data)
    for featLoop in range(n - 1):  # 每个特征
        for valLoop in set(data[:, featLoop].T.tolist()[0]):  # 每个特征值
            mat0, mat1 = binSplitTree(data, featLoop, valLoop)  # 分割
            if shape(mat0)[0] < numLim or shape(mat1)[0] < numLim:  # 预剪枝 2:节点个数少于限制 continue
                continue
            newError = errType(mat0) + errType(mat1)  # 拆分后误差
            if newError < bestError:  # 更新最小误差 并且记录特征(值)
                bestError = newError
                bestFeat = featLoop
                bestValue = valLoop
    if errorFirst - bestError < errorLim:  # 预剪枝 3:小于误差限制 返回节点均值
        return None, leafType(data)
    mat0, mat1 = binSplitTree(data, bestFeat, bestValue)
    if shape(mat0)[0] < numLim or shape(mat1)[0] < numLim:  # 预剪枝 4:小于点数目限制 返回节点均值
        return None, leafType(data)
    return bestFeat, bestValue

# 递归建树 (叶子生成方法 长度/误差限制
def creatTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1, 4)):
    feat, value = chooseBestSplit(dataSet, leafType, errType, ops)
    if feat is None:  #
        return value  # 此时 叶子节点是一个数值
    tree = {}
    lSet, rSet = binSplitTree(dataSet, feat, value)
    tree['Feat'] = feat
    tree['Value'] = value
    tree['Left'] = creatTree(lSet, leafType, errType, ops)  #
    tree['Right'] = creatTree(rSet, leafType, errType, ops)  # 左右子树递归建树
    return tree

# 回归树 估计方法
def regTreeEval(tree, data):
    return float(tree)

# 模型树 估计方法
def modelTreeEval(tree, data):
    m, n = shape(data)
    X = mat(ones((1, n + 1)))  # 增加了一列(第零列)1
    X[:, 1:n + 1] = data
    # print shape(X)
    # print shape(tree)
    return float(X * tree)

# 树预测 (树节点+数据+估计方法
def treeForecast(tree, data, Eval=regTreeEval):
    if not isTree(tree):
        return Eval(tree, data)
    # 数值 左大右小
    # 左子树
    if data[tree['Feat']] > tree['Value']:
        if isTree(tree['Left']):
            return treeForecast(tree['Left'], data, Eval)
        else:
            return Eval(tree['Left'], data)
    # 右子树
    else:
        if isTree(tree['Right']):
            return treeForecast(tree['Right'], data, Eval)
        else:
            return Eval(tree['Right'], data)

# 创建预测值 (树节点+测试集+预估方法
def creatForecast(tree, testData, Eval=regTreeEval):
    m = len(testData)
    yPre = mat(zeros((m, 1)))
    for i in range(m):
        yPre[i, 0] = treeForecast(tree, testData[i], Eval)  # 第i个点 进行预测
    return yPre

# 打印图片
def outPic(x, y, yPre, Type):
    import pylab as pl
    pl.scatter(x.tolist(), y.tolist(), s=10, c='green', marker='+')
    pl.scatter(x.tolist(), yPre.tolist(), s=15, c='red')
    pl.xlabel(Type)
    pl.show()

#
if __name__ == '__main__':
    # 加载数据
    trainMat = mat(loadData("bike_train.txt"))
    testMat = mat(loadData("bike_test.txt"))
    # 模型树
    tree = creatTree(trainMat, leafType=modelLeaf, errType=modelErr, ops=(1, 20))
    yPre = creatForecast(tree, testMat[:, 0], Eval=modelTreeEval)
    print "modelTree :", corrcoef(yPre, testMat[:, 1], rowvar=0)[0, 1]
    # outPic(testMat[:, 0], testMat[:, 1], yPre,"modelTree")
    # 回归树
    tree = creatTree(trainMat, leafType=regLeaf, errType=regErr, ops=(1, 20))
    yPre = creatForecast(tree, testMat[:, 0], Eval=regTreeEval)
    print "regTree :", corrcoef(yPre, testMat[:, 1], rowvar=0)[0, 1]
    # outPic(testMat[:, 0], testMat[:, 1], yPre,"regTree")
    # 线性回归
    ws, X, Y = linerSolve(trainMat)
    yPre = ws[1, 0].T * testMat[:, 0] + ws[0, 0]  # Y=aX+b
    print "lineReg :", corrcoef(yPre, testMat[:, 1], rowvar=0)[0, 1]
    # outPic(testMat[:, 0], testMat[:, 1], yPre,'lineReg')

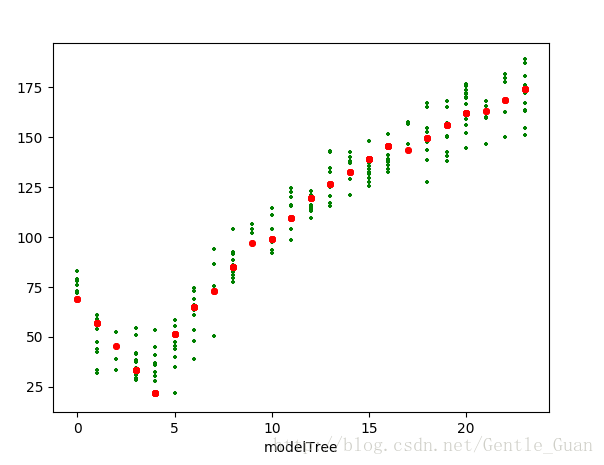
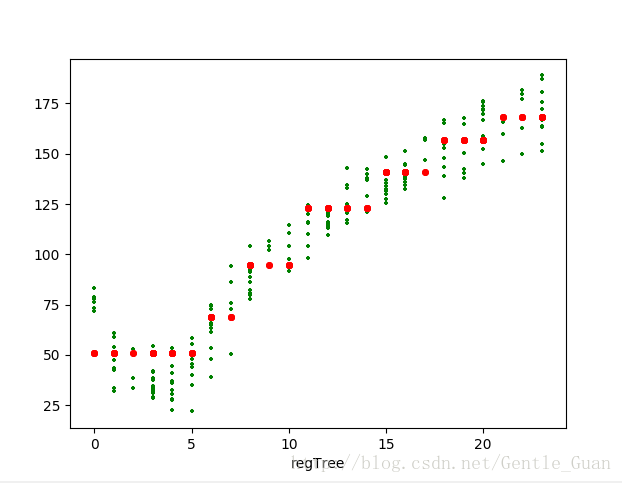
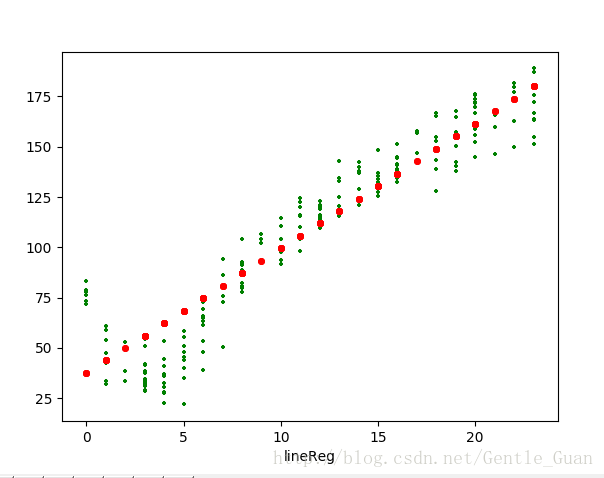
5. 图像 以及 结果分析

# modelTree : 0.976041219138
# regTree : 0.964085231822
# lineReg : 0.943468423567

观察一下 R2 很显然 模型树很强 线性回归最弱
我觉得是数据的问题
……

6. 附 数据集

额 等建网盘吧….