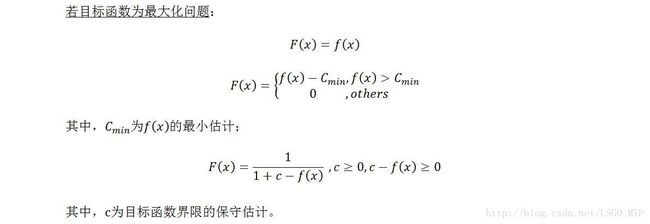遗传算法(GA)个人学习和总结(入门基础)
遗传算法解决的问题
通过模拟自然进化过程搜索最优解的方法。
也即是说,解决的问题是最优化问题,所以在解决实际问题中要看实际问题是否能转换为求解最优化问题的模型。
遗传算法的求解过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。
遗传算法的过程
过程其实很简单:是一个通过循环迭代获取最优解的过程。简易的过程如下图:

其间完整的过程解释:确定编码方式,对问题的解进行编码;初始化种群(种群中每一个个体均编码完成);评价种群中的个体(采用适应度函数进行评估,位串的解码值,目标函数值,目标函数值向适应值映射,适应值调整);判断是否满足要求(满足结束迭代,获取最优解,不满足继续进行迭代过程);进行遗传操作:选择、交叉、变异;产生新的一代种群;继续进行评价种群的个体……
1- 编码
二进制编码
定义:二进制编码方法是使用二值符号集{0,1},它所构成的个体基因型是一个二进制编码符号串。二进制编码符号串的长度与问题所要求的求解精度有关。
举例:0≤x≤1023,精度为1,m表示二进制编码的长度。则有建议性说法:使 2m-1≤1000(跟精度有关)≤2m-1。取m=10。例如:X:0010101111就可以表示一个个体,它所对应的问题空间的值是x=175。
优点:编码、解码操作简单易行;交叉、变异等遗传操作便于实现;合最小字符集编码原则;利用模式定理对算法进行理论分析。
缺点:对于一些连续函数的优化问题,由于其随机性使得其局部搜索能力较差,如对于一些高精度的问题,当解迫近于最优解后,由于其变异后表现型变化很大,不连续,所以会远离最优解,达不到稳定。
格雷码
定义:格雷码编码是其连续的两个整数所对应的编码之间只有一个码位是不同的,其余码位完全相同。它是二进制编码方法的一种变形。
十进制数0—15之间的二进制码和相应的格雷码分别编码如下。
二进制编码为:0000,0001,0010,001 1,0100。0101,0110,0111,
1000,1001,1010,1011,1100,1101,1110,1111;
格雷码编码为:0000,0001,0011,0010,0110,0111,0101,0100,
1100,1101,1111,1110,1010,1011,1001,1000。
举例:对于区间[0。1023]中两个邻近的整数X1=175和X2=176,若用长度为10位的二进制编码,可表示为X11:0010101111和X12 0010110000,而使用同样长度的格雷码,它们可分别表示为X21:0010101111和X22:0010101000。
优点:便于提高遗传算法的局部搜索能力;交叉、变异等遗传操作便于实现;符合最小字符集编码原则;便于利用模式定理对算法进行理论分析。
浮点数(实数)编码
定义:浮点数编码是指个体的每个基因值用某一范围内的一个浮点数来表示,而个体的编码长度等于其决策变量的个数。因为这种编码方法使用的决策变量的真实值,也称之为真值编码方法。
对于一些多维、高精度要求的连续函数优化问题,使用二进制编码来表示个体时将会有一些不利之处。
二进制编码存在着连续函数离散化时的映射误差。个体长度较知时,可能达不到精度要求,而个体编码长度较长时,虽然能提高精度,但却使遗传算法的搜索空间急剧扩大。
浮点法,是指个体的每个基因值用某一范围内的一个浮点数来表示。在浮点数编码方法中,必须保证基因值在给定的区间限制范围内,遗传算法中所使用的交叉、变异等遗传算子也必须保证其运算结果所产生的新个体的基因值也在这个区间限制范围内。
优点:适用于在遗传算法中表示范围较大的数;适用于精度要求较高的遗传算法;便于较大空间的遗传搜索;改善了遗传算法的计算复杂性,提高了运算交率;便于遗传算法与经典优化方法的混合使用;便于设计针对问题的专门知识的知识型遗传算子;便于处理复杂的决策变量约束条件。
符号编码法
定义:符号编码法是指个体染色体编码串中的基因值取自一个无数值含义、而只有代码含义的符号集如{A,B,C…}。
优点:符合有意义积术块编码原则;便于在遗传算法中利用所求解问题的专门知识;便于遗传算法与相关近似算法之间的混合使用。
缺点:但对于使用符号编码方法的遗传算法,一般需要认真设计交叉、变异等遗传运算的操作方法,以满足问题的各种约束村求,这样才能提高算法的搜索性能。
2- 适应度函数
定义:适应度函数(Fitness Function)的选取直接影响到遗传算法的收敛速度以及能否找到最优解,因为遗传算法在进化搜索中基本不利用外部信息,仅以适应度函数为依据,利用种群每个个体的适应度来进行搜索.因为适应度函数的复杂度是遗传算法复杂度的主要组成部分,所以适应度函数的设计应尽可能简单,使计算的时间复杂度最小。
有关适应度函数和适应度的分配,这里摘选了一篇比较好的内容来学习。
3- 选择算子
作用:对群体进行优胜劣汰造作,使适应度较高的个体被遗传到下一代群体中的概率较大,使适应度较小的个体被遗传到下一代群体中的概率较小。
常见的选择方法:
1.轮盘赌选择(Roulette Wheel Selection):是一种回放式随机采样方法。每个个体进入下一代的概率等于它的适应度值与整个种群中个体适应度值和的比例。选择误差较大。
2.随机竞争选择(Stochastic Tournament):每次按轮盘赌选择一对个体,然后让这两个个体进行竞争,适应度高的被选中,如此反复,直到选满为止。
3.最佳保留选择:首先按轮盘赌选择方法执行遗传算法的选择操作,然后将当前群体中适应度最高的个体结构完整地复制到下一代群体中。
4.无回放随机选择(也叫期望值选择Excepted Value Selection):根据每个个体在下一代群体中的生存期望来进行随机选择运算。方法如下:
(1) 计算群体中每个个体在下一代群体中的生存期望数目N。
(2) 若某一个体被选中参与交叉运算,则它在下一代中的生存期望数目减去0.5,若某一个体未 被选中参与交叉运算,则它在下一代中的生存期望数目减去1.0。
(3) 随着选择过程的进行,若某一个体的生存期望数目小于0时,则该个体就不再有机会被选中。
5.确定式选择:按照一种确定的方式来进行选择操作。具体操作过程如下:
(1) 计算群体中各个个体在下一代群体中的期望生存数目N。
(2) 用N的整数部分确定各个对应个体在下一代群体中的生存数目。
(3) 用N的小数部分对个体进行降序排列,顺序取前M个个体加入到下代群体中。至此可完全确定出下一代群体中M个个体。
6.无回放余数随机选择:可确保适应度比平均适应度大的一些个体能够被遗传到下一代群体中,因而选择误差比较小。7.均匀排序:对群体中的所有个体按期适应度大小进行排序,基于这个排序来分配各个个体被选中的概率。
8.最佳保存策略:当前群体中适应度最高的个体不参与交叉运算和变异运算,而是用它来代替掉本代群体中经过交叉、变异等操作后所产生的适应度最低的个体。
9.随机联赛选择:每次选取几个个体中适应度最高的一个个体遗传到下一代群体中。
10.排挤选择:新生成的子代将代替或排挤相似的旧父代个体,提高群体的多样性。
其中轮盘赌选择法 (roulette wheel selection)是最简单也是最常用的选择方法。在该方法中,各个个体的选择概率和其适应度值成比例。设群体大小为n,其中个体i的适应度为,则i 被选择的概率,为遗传算法 缺点:随机操作原因,误差比较大,有时连适应度较高的个体都选不上。
缺点:随机操作原因,误差比较大,有时连适应度较高的个体都选不上。
4- 交叉算子
作用:交叉算子根据交叉率将种群中的两个个体随机地交换某些基因,能够产生新的基因组合,期望将有益基因组合在一起。
根据编码表示方法的不同,可以有以下的交叉方法:
实值重组(real valued recombination)
1)离散重组(discrete recombination)
2)中间重组(intermediate recombination)
3)线性重组(linear recombination)
4)扩展线性重组(extended linear recombination)。
二进制交叉(binary valued crossover)
1)单点交叉(single-point crossover)
2)多点交叉(multiple-point crossover)
3)均匀交叉(uniform crossover)
4)洗牌交叉(shuffle crossover)
5)缩小代理交叉(crossover with reduced surrogate)
最常用的交叉算子为单点交叉(one-point crossover)。具体操作是:在个体串中随机设定一个交叉点,实行交叉时,该点前或后的两个个体的部分结构进行互换,并生成两个新个体。下面给出了单点交叉的一个例子:
个体A:1 0 0 1 ↑1 1 1 → 1 0 0 1 0 0 0 新个体
个体B:0 0 1 1 ↑0 0 0 → 0 0 1 1 1 1 1 新个体
5- 变异算子
定义:是指将个体染色体编码串中的某些基因座上的基因值用该基因座上的其它等位基因来替换,从而形成新的个体。
例如下面这串二进制编码:
101101001011001变异后:
001101011011001常用的变异方法(适用于二进制编码和浮点数编码的个体):
基本位变异(Simple Mutation):对个体编码串中以变异概率、随机指定的某一位或某几位仅因座上的值做变异运算。
均匀变异(Uniform Mutation):分别用符合某一范围内均匀分布的随机数,以某一较小的概率来替换个体编码串中各个基因座上的原有基因值。(特别适用于在算法的初级运行阶段)
边界变异(Boundary Mutation):随机的取基因座上的两个对应边界基因值之一去替代原有基因值。特别适用于最优点位于或接近于可行解的边界时的一类问题。
非均匀变异:对原有的基因值做一随机扰动,以扰动后的结果作为变异后的新基因值。对每个基因座都以相同的概率进行变异运算之后,相当于整个解向量在解空间中作了一次轻微的变动。
高斯近似变异:进行变异操作时用符号均值为P的平均值,方差为P**2的正态分布的一个随机数来替换原有的基因值。
6- 终止规则
当最优个体的适应度达到给定的阈值,或者最优个体的适应度和群体适应度不再上升时,或者迭代次数达到预设的代数时,算法终止。预设的代数一般设置为100-500代。
总结
文章是遗传算法的整个流程图和6个关键点的个人理解和结合其他资料的总结。不足之处请指出,博主正在学习GA的内容,目的是完成一个具有约束条件的优化问题,如果能顺利完成,后续会在博客中贴出实际问题、实际问题的转换模型以及实现的方案。