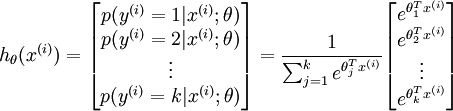机器学习入门-logistic回归和softmax回归
刚学完吴恩达-
logistic回归和softmax回归放在一起总结一下，其实softmax就是logistic的推广，logistic一般用于二分类，而softmax是多分类。
逻辑回归Logistic Regression
logistic回归要解决什么样的问题呢？假设有一训练样本集合X ＝ {x1, x2, x3, ……}，其中样本 xi 由一系列的属性表示即，xi = (a1, a2, a3,……），并且对于样本集合X中的样本要么属于类别0， 要么属于类别1,即二分类问题。举例：给你一张图片，辨别这张图片是猫（1）或者不是猫（0）。
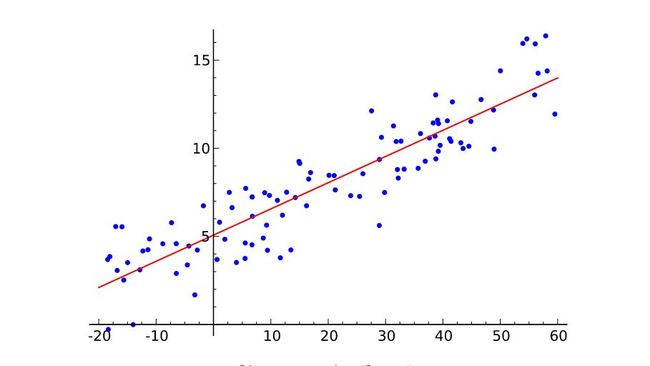
logistic函数一步步引出：现在给出X，我们希望得出Y ，很自然联想到以前学过的线性回归：（通过已知的x，y关系去推出相关函数，从而预测y的值）
不难推出：
，其中
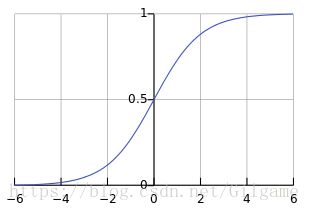
为参数，b为拦截器。但是，这就有个问题了，函数y的取值在负无穷在正无穷之间，而我们希望得到的是一个概率，图片是猫的概率（比如：0.8），不是猫的概率（0.2），即我们希望y的取值在（0,1）。于是我们引入了logistic函数：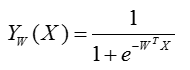
，函数图像如下：
我们发现呢，它总是介于0－1之间呢，刚好能满足我们的要求，我们可以让 Y 函数作为一种概率估计哦，而是对于一个Xi，如果它的yi=1，那么我们就用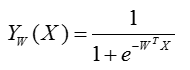这个公式映射所对应的概率，如果对于一个Xi，如果它的yi=0，那么我们就用
这个公式映射所对应的概率。都是根据yi的值映射出来一个概率。
又因为我们的Y是概率，我们不能利用最小误差等，我们这里用的是极大化所有样本的对数似然函数：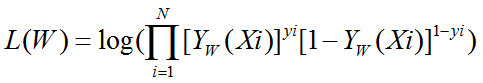
这里贴一个链接，大家可以非常通俗易懂的理解似然函数：（如侵删）：https://blog.csdn.net/linyanqing21/article/details/50939009
（对似然函数不了解的看上文）现在要求w，只需要使w的似然函数L(w)极大化，然后极大值对应的θ就是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值？当然是求导，然后让导数为0，那么解这个方程得到的w就是了（当然，前提是函数L(w)连续可微）。那如果w是包含多个参数的向量那怎么处理啊？当然是求L(w)对所有参数的偏导数，也就是梯度了，那么n个未知的参数，就有n个方程，方程组的解就是似然函数的极值点了，当然就得到这n个参数了。
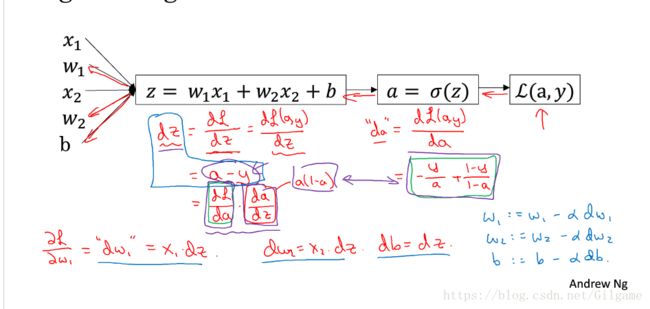
以下贴出吴恩达老师的求导并更新w的笔记：
以上即将吴恩达老师第一课第二讲知识全部串联。
归一指数函数Softmax Regression
我们上面讨论的logistic逻辑回归是针对二分类的，但如果有多种分类结果呢？假设有一训练样本集合X ＝ {x1, x2, x3, ……}，其中样本 xi 由一系列的属性表示即，xi = (a1, a2, a3,……），并且对于样本集合X中的样本属于类别C ＝ {c1, c2, c3, ……}中的一种。现在呢，我们有一个测试样本x, 我们根椐上面的知识来推断： 样本x 属于哪种类别呢？举例，给你一张图片，我让你识别是“猫”，还是“狗”，还是“牛”，还是“羊”，等等。。。
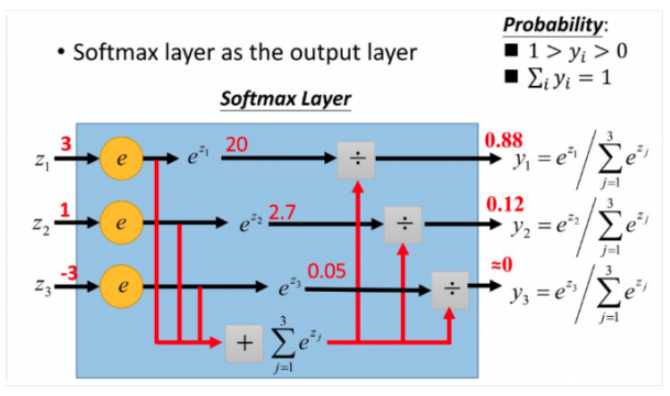
同logistic回归函数：我们需要将结果映射在（0,1）之中，即用概率表示。首先我们给出logistic函数的表示形式：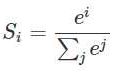
，对此公式更形象的表示如下：
原本我们的y输出为z1 = 3，z2 = 1 ，z3 = -3；通过softmax函数作用后，他就成为映射到（0,1）的值了，成为了我们想要的概率，并且保证，总和为1；
于是我们的假设函数 
形式如下：
softmax函数只推理到这里，便于理解和记忆，有想继续学习的同学请自行百度，笔者机器学习小白，日常笔记，希望各路大神多多指导。
———————————————————————————————————————————
参考资料：
【1】https://www.cnblogs.com/happylion/p/4169945.html
【2】https://blog.csdn.net/xbinworld/article/details/45291009
【3】https://blog.csdn.net/linyanqing21/article/details/50939009
【4】https://www.cnblogs.com/alexanderkun/p/8098781.html