机器学习（三）——Linear Discriminant Analysis

二分类情况：

1． 加载实验数据
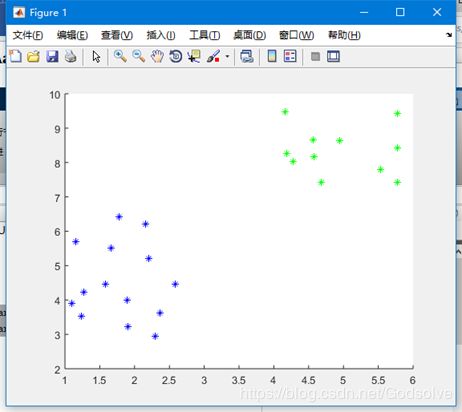
2. 绘制出数据散点图

3. 求类内散度矩阵

4. 求类间散度矩阵

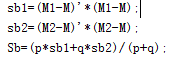
5. 求最大特征值和特征向量

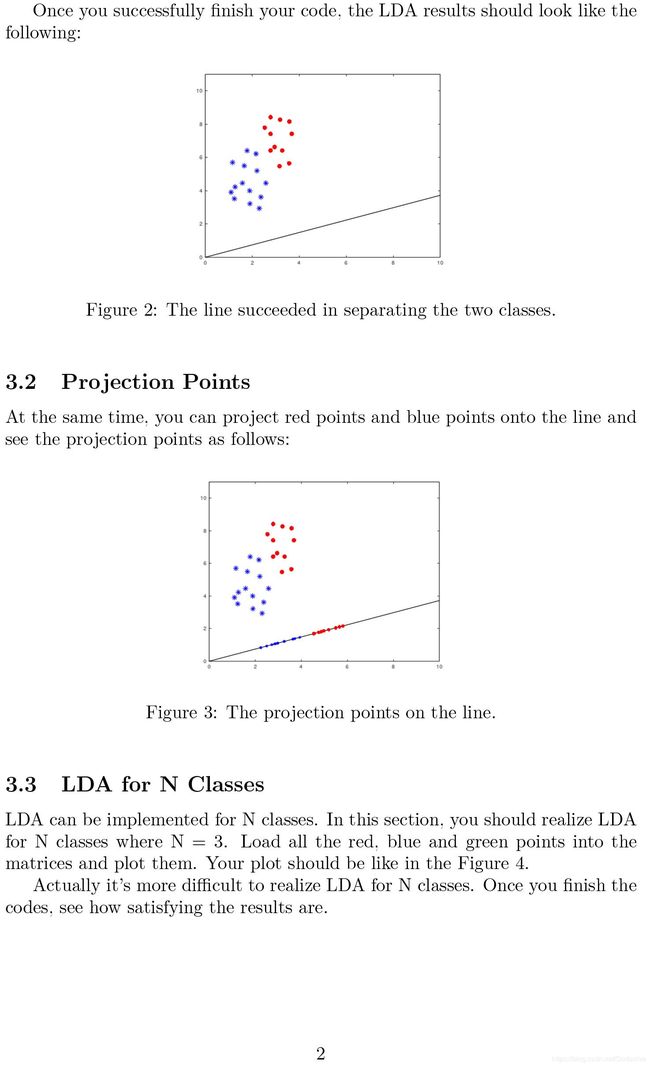
6. 计算投影点

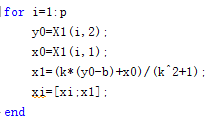
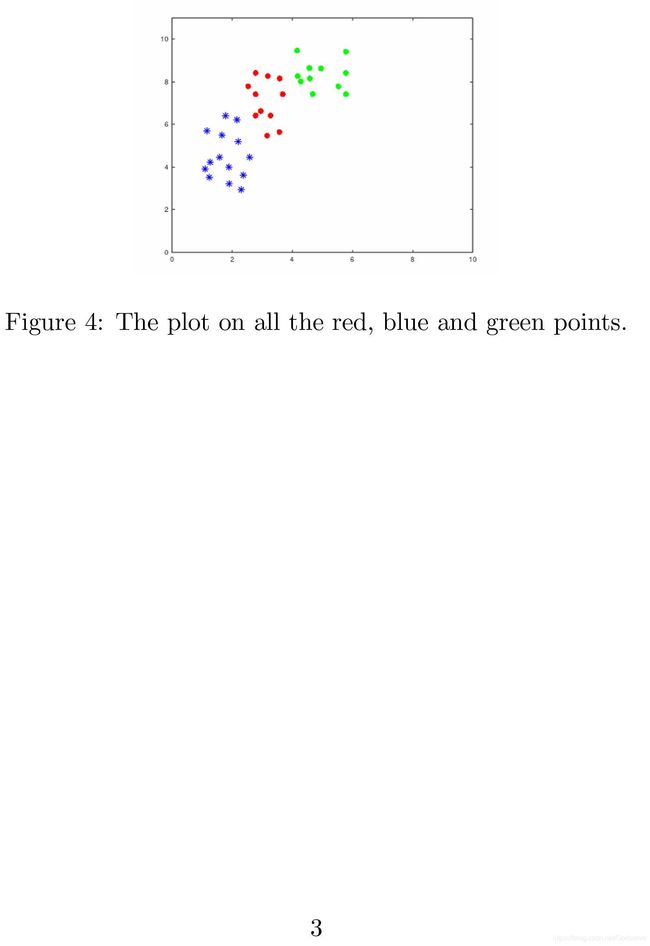
7. 绘制完整图像

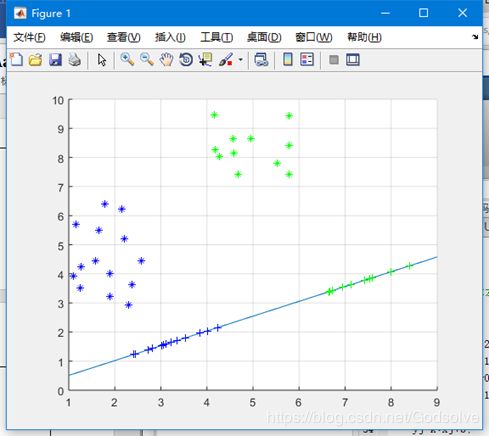
多分类情况：

多分类线性判别分析（LDA）中，除了参数有所变化之外，只对求最大特征值及特征向量的部分做了些许改动，类间散度矩阵和类内散度矩阵都由(psb1+qsb2)/(p+q)变成了(psb1+qsb2+r*sb3)/(p+q+r)，其他部分基本相同。
最终结果：

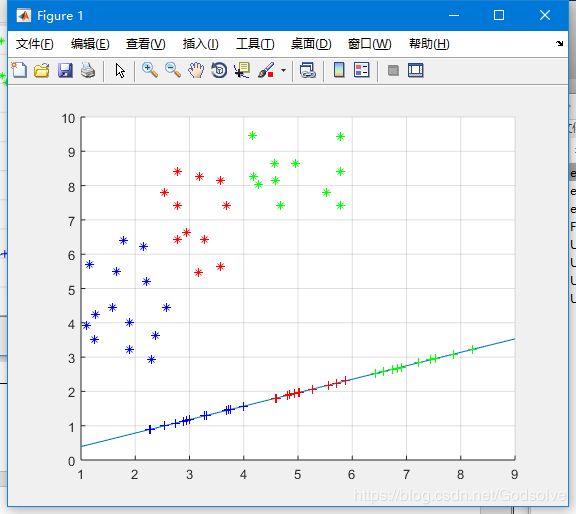
LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。

多分类LDA算法流程：

输入：数据集D={x(1),x(1),…,x(m)}D={x(1),x(1),…,x(m)}；

输出：降维后的样本集D’D′；

计算类内散度矩阵SwSw和类间散度矩阵SBSB；
计算矩阵S−1wSBSw−1SB的特征值；
找出矩阵S−1wSBSw−1SB最大的kk个特征值和其对应的kk个特征向量(w1,w2,…,wk)(w1,w2,…,wk)；
将原始样本集投影到以(w1,w2,…,wk)(w1,w2,…,wk)为基向量生成的低维空间中(k维)，投影后的样本集就是我们需要的样本集D’D′。

在本次实验中，实验要求是完成三分类LDA，而我将二分类和三分类LDA的图像做了对比，发现在三分类LDA中，投影线的斜率要更小一些。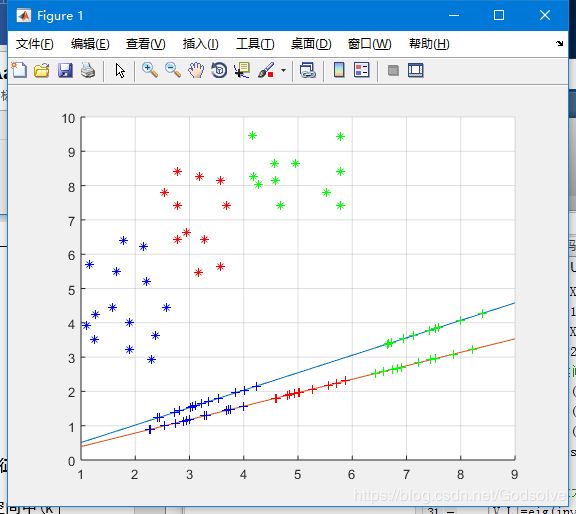

---

同时也欢迎各位关注我的公众号 南木的下午茶

---

附录：程序源代码
X1=load('ex3blue.dat');
X2=load('ex3green.dat');
X3=load('ex3red.dat');
hold on
plot(X1(:,1),X1(:,2),'b*','markerfacecolor', [ 1, 0, 0 ]);
plot(X2(:,1),X2(:,2),'g*','markerfacecolor', [ 0, 0, 1 ]);
plot(X3(:,1),X3(:,2),'r*','markerfacecolor', [ 0, 1, 0 ]);
grid on
M1 = mean(X1);
M2 = mean(X2);
M3 = mean(X3);
M = mean([X1;X2;X3]);
%µÚ¶þ²½£ºÇóÀàÄÚÉ¢¶È¾ØÕó
p = size(X1,1);
q = size(X2,1);
r = size(X3,1);
a=repmat(M1,14,1);
S1=(X1-a)'*(X1-a);
b=repmat(M2,14,1);
S2=(X2-b)'*(X2-b);
c=repmat(M3,14,1);
S3=(X3-c)'*(X3-c);
Sw=(p*S1+q*S2+r*S3)/(p+q+r);
%µÚÈý²½£ºÇóÀà¼äÉ¢¶È¾ØÕó
sb1=(M1-M)'*(M1-M);
sb2=(M2-M)'*(M2-M);
sb3=(M3-M)'*(M3-M);
Sb=(p*sb1+q*sb2+r*sb3)/(p+q+r);
bb=det(Sw);
%µÚËIJ½£ºÇó×î´óÌØÕ÷ÖµºÍÌØÕ÷ÏòÁ¿
[V,L]=eig(inv(Sw)*Sb);
[a,b]=max(max(L));
W = V(:,b);%×î´óÌØÕ÷ÖµËù¶ÔÓ¦µÄÌØÕ÷ÏòÁ¿
%µÚÎå²½£º»­³öͶӰÏß
k=W(2)/W(1);
b=0;
x=1:9;
yy=k*x+b;
plot(x,yy);%»­³öͶӰÏß
%¼ÆËãµÚÒ»ÀàÑù±¾ÔÚÖ±ÏßÉϵÄͶӰµã
xi=[];
for i=1:p    
    y0=X1(i,2);    
    x0=X1(i,1);    
    x1=(k*(y0-b)+x0)/(k^2+1);    
    xi=[xi;x1];
end
yi=k*xi+b;
XX1=[xi yi];
%¼ÆËãµÚ¶þÀàÑù±¾ÔÚÖ±ÏßÉϵÄͶӰµã
xj=[];
for i=1:q    
    y0=X2(i,2);    
    x0=X2(i,1);    
    x1=(k*(y0-b)+x0)/(k^2+1);    
    xj=[xj;x1];
end
yj=k*xj+b;
XX2=[xj yj];
%¼ÆËãµÚÈýÀàÑù±¾ÔÚÖ±ÏßÉϵÄͶӰµã
xk=[];
for i=1:q    
    y0=X3(i,2);    
    x0=X3(i,1);    
    x1=(k*(y0-b)+x0)/(k^2+1);    
    xk=[xk;x1];
end
yk=k*xk+b;
XX3=[xk yk];
% y=W'*[X1;X2]';
plot(XX1(:,1),XX1(:,2),'b+','markerfacecolor', [ 1, 0, 0 ]);
plot(XX2(:,1),XX2(:,2),'g+','markerfacecolor', [ 0, 0, 1 ]);
plot(XX3(:,1),XX3(:,2),'r+','markerfacecolor', [ 0, 1, 0 ]);