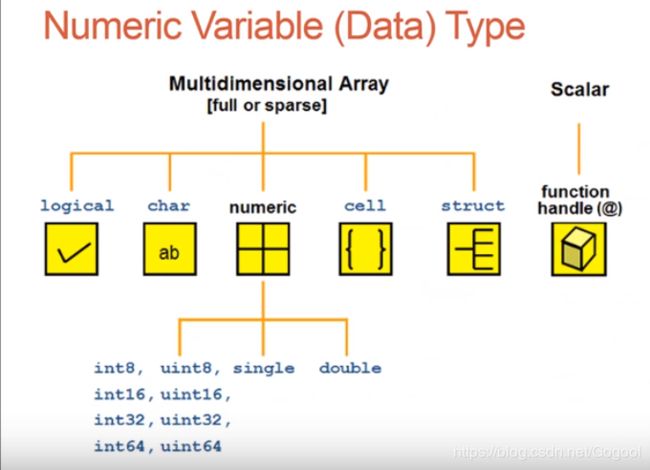
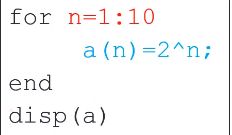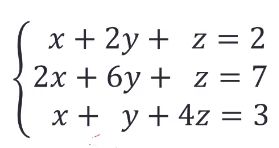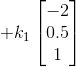台大matlab教程知识点——小整

目录

一、基础

二、矩阵

 三、逻辑语句                             

四、structure&cell

五、FILE ACCESS

六、基础绘图

七、三维绘图

八、GUI制作

九、影像处理

十、微积分

十一、方程式求根

十二、线性回归方程式

十三、线性系统

十四、统计

         十五、回归与内插

---

 

        这套视频里面讲解了matlab基本操作、应用函数以及学习方法，蛮适合新手入门的，在后期视频中，数学原理讲解偏多，主要是为了对比不同解法函数的区别，以便在后期应用中选择合适的函数应用，像numeric和symbolic两种方式求方程根的对比等。总体看完能建立一个基本框架，懂得如何操作和后期学习方法，后期学习主要还是靠自己多查阅文档，matlab官网提供了很好的自学平台，有详细的函数使用说明文档和社区答疑等等。用熟练了也是个很强的工具。

一、基础

1、matlab变量

可以去这个网站查找matlab里的函数

https://ww2.mathworks.cn/help/matlab/referencelist.html?type=function&category=index&s_tid=CRUX_function_index

                                   

2、matlab变量定义

①定义变量注意事项：atlab里的关键字：定义变量时不能用，如下图

>>iskeyword    %查询关键字

     

( eps:很小很小的数，对应inf无穷)

>>clear    %消除定义变量：  eg：clear a，危险慎用

 >>clc       %  清屏，但变量不清除

>>who      % 显示已经定义了哪些变量

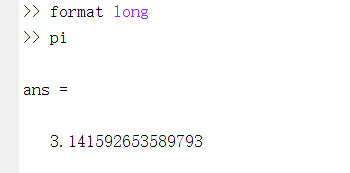
 3、变量显示格式——format

format有不同的显示格式。应用时键入format再输入变量即可自动转换。如：

rat是以分数显示

   

二、矩阵

1、定义 横向矩阵a=[1 2 3 4]

              纵向矩阵b=[1;2;3;4]

a*b 1*1，b*a 4*4

a= 1  2   3   4   

     5  6   7   8 

     9  10  11  12

选取矩阵对象

某个数

>>a(2,3)   

>>a(8)    %  a(8)是因为它是按列数的，第8个数字

某行某列

>>a(2,:)     %第2行

>>a(:,2)     %第2列

自定义

注：没有逗号的a括号里面的数字按列数第i个，括号里啥形式，输出的矩阵啥形式，列12

       有逗号的逗号前代表行，逗号后代表列，输出两者的交集对应点。矩阵形式同样道理。列3

①>>a([1 3 5])         输出：[1  9  6]

②>>a([1  3];[2  3])  输出：[1  9;5  9]  分号前代表第1、3个数字，分号后代表第2、3个数字

③>>a([1  3],[2  3])  输出：[1  2;9  10]  逗号前代表第1、3行，逗号后代表第2、3列，它们的交集就是输出

替换矩阵数字

>>a(1,2)=72    %如替换第一行第二列数字成72

colon operator

生成等比数列： 可以加括号，也可以不加，操作还可以用于str

>>a=1:100                  %1,2,3,4...100

>>b=1:2:100               %1,3,5,...,99

挡掉/增添矩阵某一行 /列

>>A(3,:)=[]                    %去掉A矩阵第三行

>>A(3,:)=[9 10 11 12]    %增添A矩阵

增添行增列去掉第三行

增广矩阵

>>F=[A B]/[A,B]

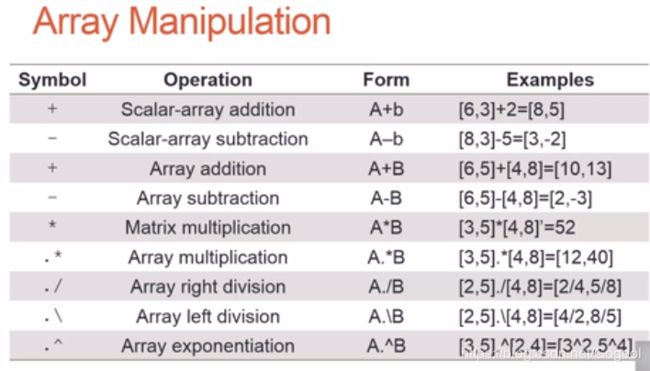
矩阵加减乘除

                                                

转置矩阵

>>C=A’

其他函数

>>max(A)  = 14     5     3         %矩阵中行总和最大的行

>> max(max(A))  ans =14       %所有值中max

>>sum(A)       %列sum

>>sort(A)          %列排序               

>>sortrows(A)   %行排序

>>size(A)          %矩阵行列

>>find(A==?)     %返回A中目标值的行列，常用

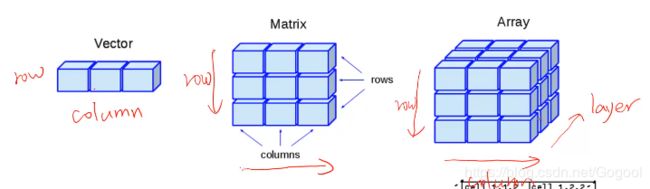
[X Y]=find(A==5)

三维矩阵

                      

>>

A{row  columns  layer}前两个跟二维矩阵顺序一样

cat()函数

连接矩阵，cat(1\2\3,A,B) 1\2\3分别代表 row columns layer连接，A和B是矩阵

reshape()函数

A 2*2矩阵

>>C=reshape(A,1,4)

C 1*4矩阵  （将A矩阵改为。。矩阵）

 三、逻辑语句                             

>>if elseif else语句

>>switch

>>while

>>for

逻辑判断

                                                    

string

>>联立单词成句子用上面string，下面组合必须长度相同

str=“ancadf”

 >> str（2）

ans=n

>>'a'==str  

ans=1 0 0 1 0 0  (扫描一遍str，是a的字符为true，反之false)

>>str(str=='a')='z'  

str= "znczdf"  (将所有a替换成z)

如何比较字符串？

将一个字符串逆置?

四、structure&cell

structure创建

直接赋值方法创建结构体

circle.radius=3.0;
circle.center=[0 0];
circle.color='red';
circle.linestyle='--'

struct()函数创建结构体

data1={3.0,5.0,'sqrt(7)'};
data2={'--''...''-.-'};
data3={'red''blue''yellow'};
data4={'yes''no''no'};
circle=struct('radius',data1,'linestyle',data2,'color',data3,'filled',data4)

cell

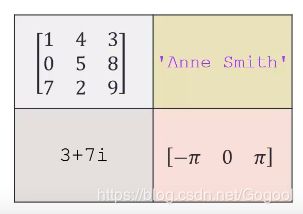
建立承受不同types的矩阵，相当于指针，指向不同的type。用{ }表示

>>建立这样的矩阵    

>>A(1,1)

ans=[3*3 double]  无意义

>>A{1,1}

ans=1 4 3

        0 5 8

        7 2 9

>>A{1,1}(1,1)

ans=1   将A{1,1}看作整体

五、FILE ACCESS

save()函数

存储工程里的变量数据>>

clear;a=magic(4);

save mydata.dat     %存储且不能用记事本阅读内容

(or)save mydata.dat -ascii    %存储且能阅读

load()函数   （和save相反）

调用储存的变量数据>>

load('mydata.mat')     %带变量名称

(or)load('mydata.mat','-ascii')     %不带变量名称

xlsread()函数

score=xlsread('**.xls');    %只读到数字部分

  score=xlsread('**.xls','A1:A6')；

xlswrite()函数

fopen()函数 /fprintf

matlab中生成.txt格式文件

效果：

fscanf()函数

调入文件中的值

六、基础绘图

二维	三维	功能
scatter	scatter3	离散图
plot	plot3、mesh...	函数、打点离散
ezplot		显函数、隐函数、参数方程

plot()函数

eg1:

>>plot(cos(0:pi/20:2*pi))   %绘制一个余弦函数    0：pi/20：2*pi分别代表 起点、步长、终点

eg2:  (搜索line，画法很多，这个好，利用向量画)

x = linspace(0,10);
y = [sin(x) cos(x)];
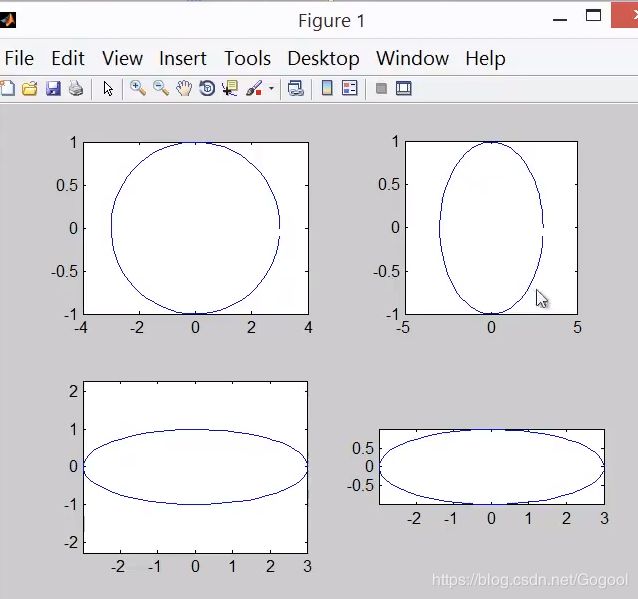
line(x,y)

ezplot()函数  （画显函数、隐函数和参数方程）

>>ezplot('sin(x)')
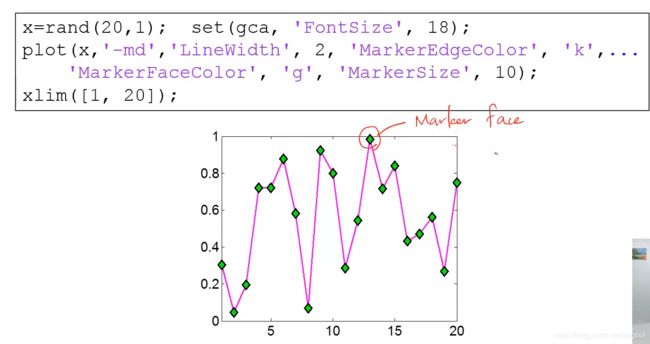
调整线条外观(打点形状、线形、颜色)

plot(x,y,'str')   %'str'顺序分别是打点形状、线条颜色、线形

eg:

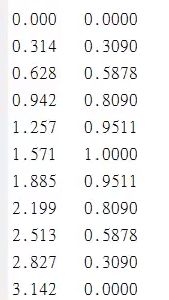
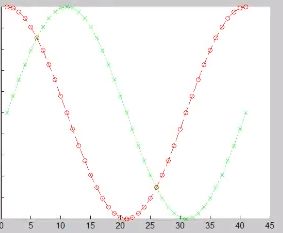
>>x=0:pi/20:2*pi

    y=cos(x);z=sin(x);

    plot(x，y，'or--'，x，z，'xg:')  ；

效果如下：

scatterplot()

绘制散点图，圈圈形式，很好看。官网上一个例程，x、y参数后面其他参数改变显示效果：

x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
c = linspace(1,10,length(x));
scatter(x,y,[],c)  %x、y 和 c 中的相应元素确定每个圆形的位置和颜色。

效果：

加图名、xy轴名称、线条名称

lengend('cos(x)','sin(x)');

    table('三角函数')；

    xlabel('x');

    ylabel('y');

y=exp(-x)的ylabel标注

ylabel('value of e^{-x}')

效果

y=sin(x)的xlabel标注

xlabel('t=0 to 2\pi')  %不是除号

效果

加注释

>>text(x，y，str，'Interpreter','latex');  %只改前三个，xy注释坐标，str内容

>>annotation('arrow','X',[x1 x2],'Y',[y1 y2]);   %第一个画箭头，3 箭头x范围 5 箭头y范围

figure adjustment

h=plot(x,y,'g-');
get(h)  %获取图像信息
get(gca)  %获取坐标信息
set(gca,xlim,[0,2*pi])   %查看完了get，从get里挑要改变的东西，信息扔第一个，要改的第二个，改成啥第三个

修饰线条颜色等可直接在plot里改

多图绘制

1、在一个坐标轴里绘制多个图，绘制hold里所有曲线，如果不加hold，只绘出最后一条

>>hold on

    plot(cos(0:pi/20:2*pi));

    plot(sin(0:pi/20:2*pi));

    hold off

 

2、在一个figure里画多个图

subplot(m,n,x)  %m几行，n几列，x第几个图（1—m*n）

subplot(2,2,1) plot(x,y1);
subplot(2,2,2) plot(x,y2);
subplot(2,2,3) plot(x,y3);
subplot(2,2,4) plot(x,y4);

3、在不同的figure里画图

figure(1)
plot(x,y1)
figure(2)
plot(x,y2)

grid axis box

以下操作只能操作最后一个图

grid on/off  打开/关闭格线

box on/off 

grid on/off  关闭后只剩下函数图

保存图片

saveas(gcf,'lala','jpeg')  %第三个查看文档，可以保存为很多种格式

七、三维绘图

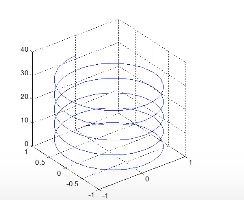
plot3()函数

适合线条型函数，eg

t=0:pi/50:10*pi;
plot3(sin(t),cos(t),t);
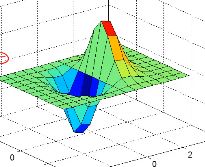
grid on;axis square;

mesh()函数&surf()函数

X、Y的维度必须和Z的列、行相同！！或者三者维度全部相同，用meshgrid()将XY处理。

适合面型，eg：

I=-2:1:2;
J=-2:1:2;
[X,Y]=meshgrid(I,J);    
Z=X.*exp(-X.^2-Y.^2);
mesh(X,Y,Z);/surf(X,Y,Z);

contour()函数—等高线

contour(X,Y,Z);

调整间距

contour（X,Y,Z,[-0.45,0.05,0.45]）;

显示等高线高度

[c,h]=contour(Z);

clabel(c,h);

上色

contourf(Z);

meshc()函数&surfc()函数

在一张图中显示等高线和立体图

view()函数

调整显示角度

>>view(45,30)；

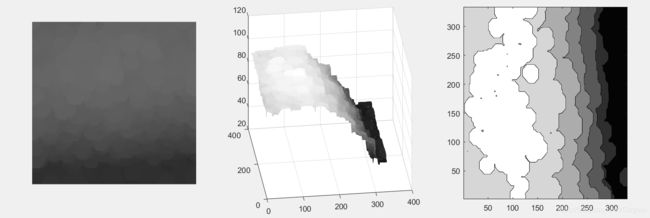
                                       灰度图   灰度图灰度值三维图(xy为像素点坐标，z为灰度值)   灰度值等高线(上色了)

https://www.cnblogs.com/hyb221512/p/9336059.html三维图形着色，很不错

八、GUI制作

共有.m和.fig两个文件

>>guide    %出现制作界面

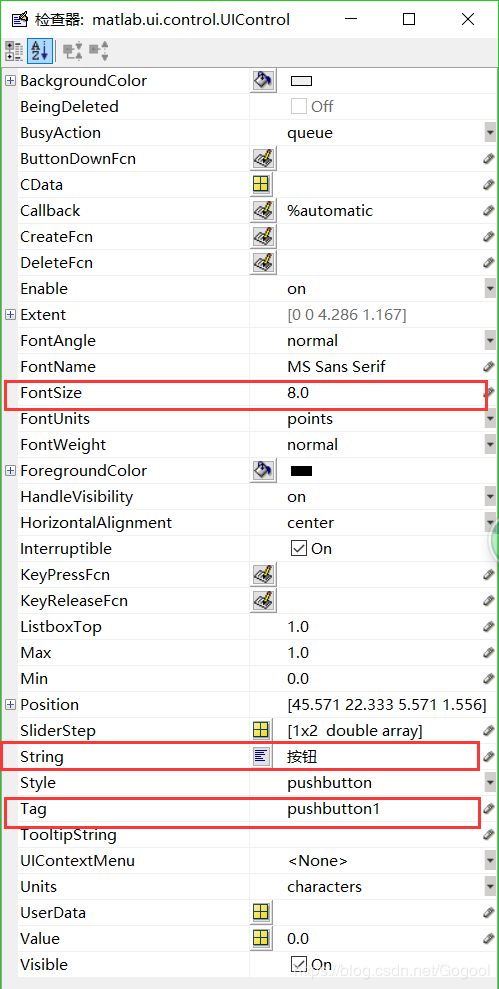
1、双击修改选择的模块

fontsize：改字体字号

string：显示名字

tag：在.m文件里自定义对象的名字

2、设置对齐

可设置各种对齐和间距

3、修改好后点击，保存后会生成.fig和.m两个文件，在.m里进行自定义设置功能，点击运行即可更改

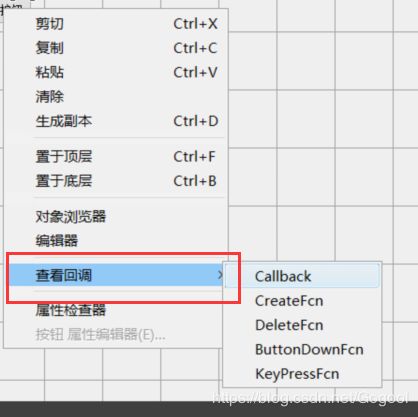
4、快速定位要设置功能的模块函数

右键模块，查看回调前往，前往之前看一眼模块的tag，修改时用。

5、全部功能实现后想在外界运行，命令行窗口键入deploytool

>>点第一个

>>点

>>点

>>保存等待，生成文件夹后点for_testing

>>OK

九、影像处理

写入图片

>>imread(' ....jpg')

展示图片

>>imshow(' ...jpg')

修改图片

I=imread('大米.jpg');
for i=1:size(I,1)
    for j=1:size(I,2)   %size( ,1)行，size( ,2)列
        if rem(i,2)==0 && rem(j,2)==0   %rem求余函数，i被除数，2除数
         I(i,j)=0;   %偶数像素设黑色
        end
    end
end
imshow(I);

灰度图看像素灰度分布（获取的图片矩阵必须是二维的，RGB等是三维）

>>imhist(I);

旋转图片

>>imrotate(I,90,'bilinear');

储存图片

>>imwrite(I,'lala.jpg');

影像处理—识别米粒

1、二值化

S=imread('3.jpg');
%RGB转灰度
I=rgb2gray(S);
%剔除背景暗亮影响
bg=imopen(I,strel('disk',15));  %选出背景，
I2=imsubtract(I,bg);           %减掉背景，去掉背景的亮暗，影响二值化
%二值化
level=graythresh(I2);          %自己找出二值化的阈值
bw=im2bw(I2,level);
imshow(bg);

剔除背景前和剔除后二值化效果，很明显

2、数米粒

归一化：扫描每个像素点，当有一个像素点符合时，判断其右边和下边像素是否也符合，如果符合，归为一个米粒

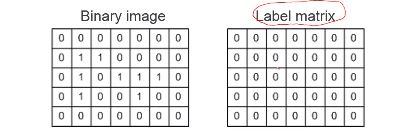
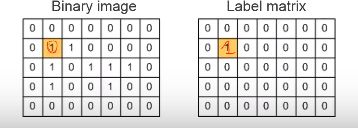
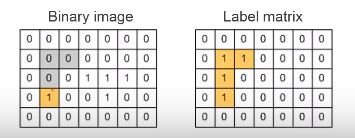
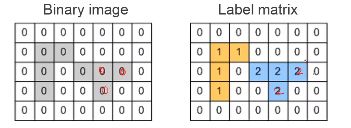
[labeled,numObjects]=bwlabel(bw,8);

只需要一句函数，原理如下：

① 扫描像素点

②找到一个，在该点立个flag（方便找完后在这个点继续寻找下一颗米粒）将原图中该像素清0，label matrix相同位置置n(第n个米粒)

标记好后，扫描右边和下边像素是否也符合，如符合，重复23两步

④右边下边都没了，回到flag点，继续扫描，寻找下一个米粒，直至全部扫描完。

3、依据区间估计挑出叠加的米粒

有些米粒因为像素点连在一起，误认为是一颗米粒，由于米粒大小基本呈正态分布，采用区间估计，挑出叠加的米粒并分开。

①每个米粒的大小

regionprops函数

graindata=regionprops(labeled,'basic');
area=graindata.Area;

循环法

num=zeros(numObjects,2);
for i=1:size(labeled,1)
    for j=1:size(labeled,2)
        if labeled(i,j)>0
            num(labeled(i,j),1)=num(labeled(i,j),1)+1;
        end 
    end
end

②米粒大小置信区间

     

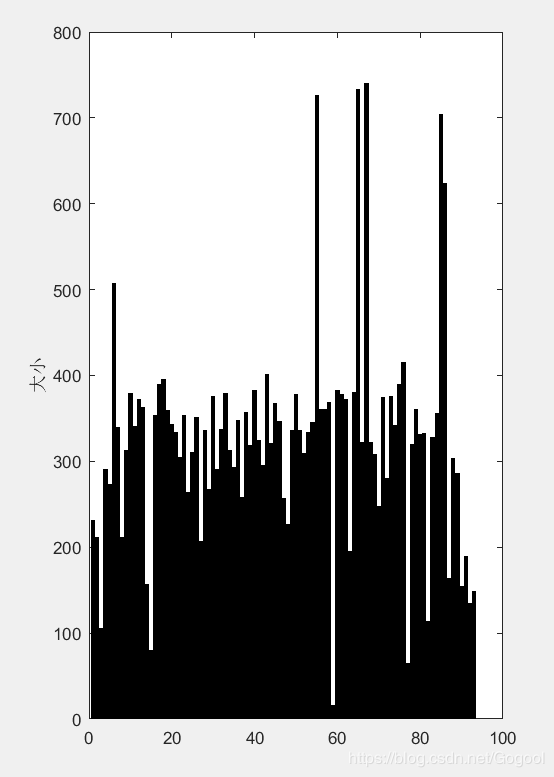
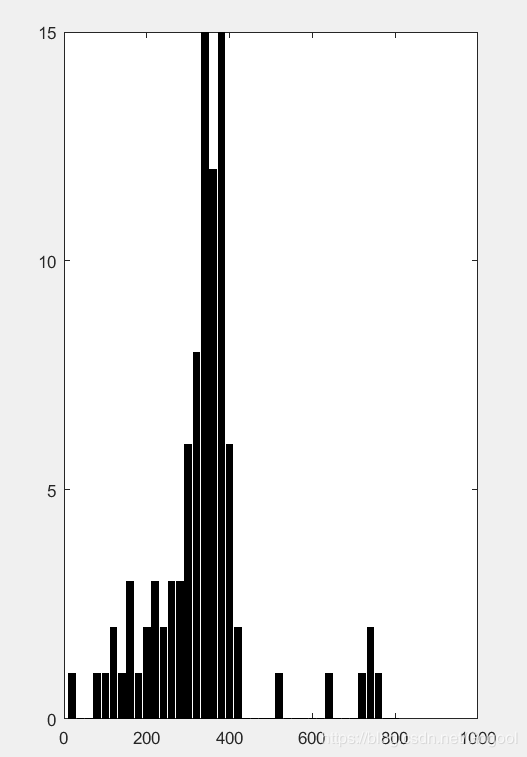
每颗米粒大小                              米粒大小分布

ps：观察米粒呈正太分布方法：划分米粒大小的区间，统计各区间米粒数，在这里观察米粒大小分布后，以20为单位划分并统计数量。

利用正态分布区间估计米粒大小的置信区间，确定米粒大小的点估计值

alpha=0.05;
[mu,sig,muci,sigci]=normfit(num,alpha);

mu为米粒的点估计值。

④ 扫描所有米粒，挑出叠加在一起的，在原有统计数量上加。

des=zeros(40,1);
di=20:20:800;
for i=1:numObjects
   des(floor(num(i,1)/20)+1,1)= des(floor(num(i,1)/20)+1,1)+1;
   if num(i,1)/mu(1,1)>1.5
       numrice=numrice+round(num(i,1)/mu(1,1))-1;
   end
end

numrice即最终米粒数

拓：bwselect()函数可以选米粒

总：

S=imread('3.jpg');
%RGB转灰度
I=rgb2gray(S);
% imhist(H);
%剔除背景暗亮影响
bg=imopen(I,strel('disk',15));  %选出背景y = feval(fittedmodel,x)
I2=imsubtract(I,bg);           %减掉背景
%二值化
level=graythresh(I2);
bw=im2bw(I2,level);
%numObjects是米粒数量（初始）
[labeled,numObjects]=bwlabel(bw,8);
num=zeros(numObjects,1);
%graindata(i).Area是第i个米粒的大小
graindata=regionprops(labeled,'basic');
for i=1:numObjects
    num(i,1)=graindata(i).Area;
end
%区间估计米粒大小置信区间
alpha=0.05;
[mu,sig,muci,sigci]=normfit(num,alpha);
numrice=numObjects;
des=zeros(40,1);
di=20:20:800;
%挑出叠加的米粒
for i=1:numObjects
   des(floor(graindata(i).Area/20)+1,1)= des(floor(graindata(i).Area/20)+1,1)+1;  %统计米粒大小的正态分布
   if graindata(i).Area/mu(1,1)>1.5
       numrice=numrice+round(graindata(i).Area/mu(1,1))-1;
   end
end
w=1:93;
subplot(1,2,1);
bar(di,des);
subplot(1,2,2);
%鼠标点，enter
obj=bwselect(bw);
imshow(obj);

十、微积分

微分

poly系列—利用系数单纯求导系数

1、ployder()函数—一次求导

p=[5 0 -2 0 1];
polyder(p);


ans=[20 0 -4 0];

2、polyint()函数—一次积分

3、polyval—高阶微分、积分

polyval(polyder(p),3);   %三阶求导
polyval(polyint(p),3);   %三阶求积

diff()函数

>>diff(f(x))—x的一阶导数

>>diff(f(x),n)—x的n阶导数

>>diff(f(x,y),x)—x的偏导

>>diff(f(x,y),x,n)—x的n阶偏导

syms x;
f(x)=sin(x)+x^2;
f=diff(f(x));

积分

初等函数积分

定积分

>>int(f,a,b)  %x范围[a,b];

不定积分

>>int(f)

syms x
y=sin(x);
f1=int(y);
f2=int(y,0,pi);

数值积分（非初等/离散型）

1、梯形型积分

>>trapz(x,y)

x=0:pi/100:pi;
y=sin(x);
s=trapz(x,y);

2、intergral()函数

①一重积分

>>integral(f,a,b)    %y用指针  自变量x要定义

syms x
f=@(x)sin(x);
s=integral(f,0,pi);

②二重积分

>>intergral2(f,a1,b1,a2,b2)  %1是外面积分，2里面

syms x y;
f=@(x,y)sin(x).*y;
integral2(f,pi,2*pi,0,pi);

>> I=dblquad(f,a,b,c,d,tol,trace)

③三重积分

>>intergral3(f,a1,b1,a2,b2,a3,b3)

3、其他

 自适应Gauss-Kronrod数值积分

>> z = quadgk(Fun,a,b)

 积分法矢量化自适应simpson数值积分

>>z = quadv(Fun,a,b)
      一次可以计算多个积分

 高精度Lobatto积分法

 >>z = quadl(Fun,a,b)

基于变步长辛普森法计算积分

>>[I,n]=quad(‘fname’,a,b,Tol,trace)

ac=@(x)sin(x)./x
s=quad(ac,pi/4,pi/2)

十一、方程式求根

Symbolic&Numeric优缺点

symbolic：不一定会有解，但有解就是准确结果。标识：定义syms x

numeric：无限逼近原则，一定会有解，但不一定是准确值。标识：y=@(x) ...

Symbolic Root Finding

solve()

%一元
syms x
y=x*sin(x)-x;
solve(y,x);

%二元，要是线性方程组，用矩阵方法方便些
syms x y
eq1=x+y;
eq2=x-2*y+2l
solve(eq1,eq2,x,y);

%带参数表示
syms a b x
solve('ax^2+b',x);   %表示x
solve('ax^2+b',b);   %表示b

Numeric Root Finding

fsolve()&fzero()

求函数零点，都是数值解，重复计算，无限逼近法。两者都只能返回一个零点！！取决于预测值靠近哪个零点

区别：fzero只能求过零点的，切于零点的不算。fsolve可以。

f=@(x)x.^2-1;
options=optimset('MaxIter',1e3,'TolFun',1e-10);   %1e3:递归次数 1e-10:误差
fsolve(f,0.1,options);
fzero(f,0.1,options);

roots()——多项式根的求解

 roots([1 -3.5 2.75 2.125 -3.875 1.25])

十二、线性回归方程式

性质法：

Ax=B  x=A’B

A=[1 2 1;2 6 1;1 1 4];
B=[2;7;3];
x=A\B;        %左除！ 
或x=inv(A)*B    

演算较复杂。

linsolve()

A=[1 2 1;2 6 1;1 1 4];
B=[2;7;3];
x=linsolve(A,B) 

rref()

A=[1 2 1;2 6 1];
B=[2;7];
x=rref([A B]) 

rref将AB增广后，得到的是行阶梯矩阵，如图：

则通解就是

B区是特解，A区非单位矩阵的列取反，未知量取0\1（取决于是否在对角线处）

十三、线性系统

线性系统和线性回归方程不一样。

线性回归方程：Ax=B，求x。

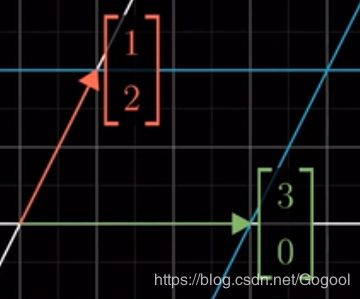
线性系统：A=，求特征值和特征向量。

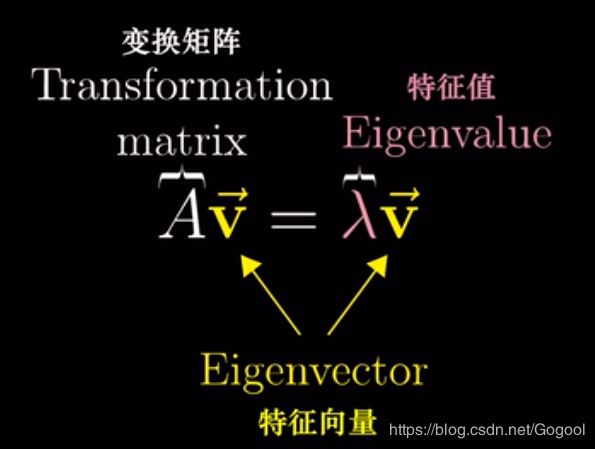
特征值和特征向量

特征向量，可以将A的每列理解成基向量，如，如图所示：

                                                                          

是特征根，其意义是在正交轴的特征向量经过在A变换矩阵中长度的变换倍数。详细理解可见https://www.bilibili.com/video/av6540378/

                                                                       

求特征值和特征向量如下：

A=[2 -12;1 5];
[v,d]=eig(A);   %v特征向量 d特征值

十四、统计

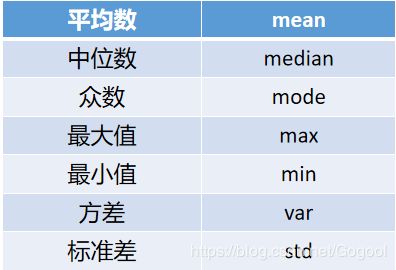
叙述统计

                                                                      

load stockreturns;
x=stocks(:,4);
a=max(x);
b=min(x);
c=std(x);
...

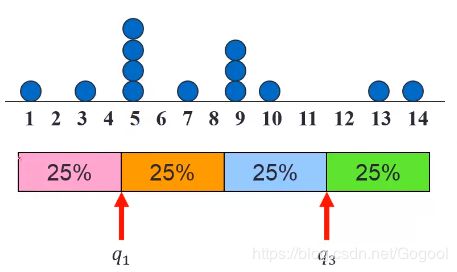
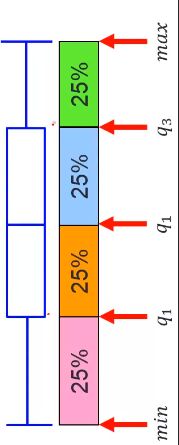
quartile—四分点

一般☞q1和q3，按位置25%和75%地方的数字，50%就是中位数。

统计绘图

直方图类

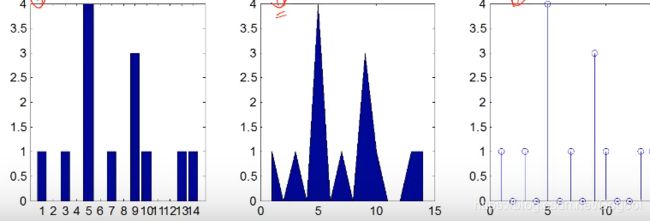
x=1:14；
freqy=[1 3 5 5 5 5 7 9 9 9 10 13 14];
s=tabulate(freqy(:));
bar(s(:,1),s(:,2));xlim([0 15]);
area(s(:,1),s(:,2));xlim([0 15]);
stem(s(:,1),s(:,2));xlim([0 15]);

绘出图形分别如下所示，中间的会有两个三角形挤在一起的情况（10处）。

这里转载的各种元素统计很不错：https://blog.csdn.net/ljyljyok/article/details/81461859

boxplot

boxplot图含义如下所示：可以显示中位数等的图，适合不同列数据的对比。

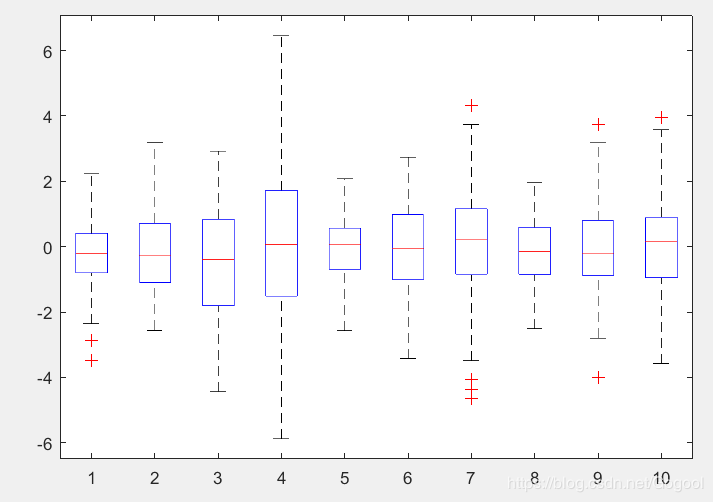
画了一个股票的boxplot。

load stockreturns;
boxplot(stocks);

 

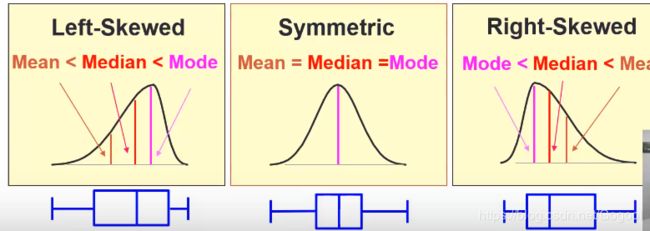
boxplot的形状含义如下，它的偏态（Skewness）

偏态（Skewness）

偏态量度对称性，skewness=0对称。众数是峰值，中位数位置不变，平均值<中位数左偏，反之右偏。

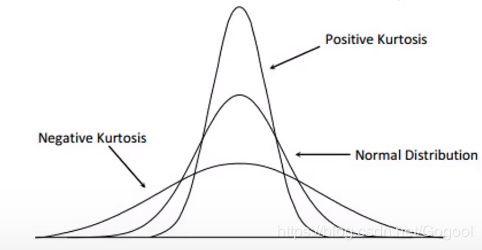
skewness(x);

峰值（kurtosis）

描述分布平整度。

这里有对偏态和峰值的详细介绍http://blog.sciencenet.cn/blog-1148346-786610.html。

推论统计

推论统计牵扯的是假设检验像t检验、z检验等，和各种参数估计如最大似然估计、区间估计等，这方面我应用还不够多，等再多理解后补充。

https://blog.csdn.net/matlab_matlab/article/details/55802815这里面总结了参数估计于假设的类型，还蛮详细的。

http://blog.sciencenet.cn/blog-292361-1017309.html这里详写了matlab的假设检验函数。

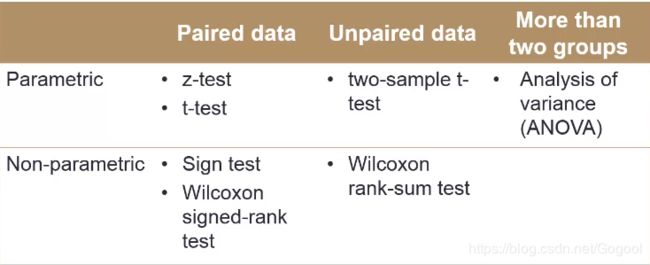
下图是教授整理的常用检验

 

十五、回归与内插

回归

polyfit()—一个变量

基于最小二乘法曲线拟合原理，构造解析函数。只能用于polyfit输出的是多项式系数，配合ployval求出f(x)值。

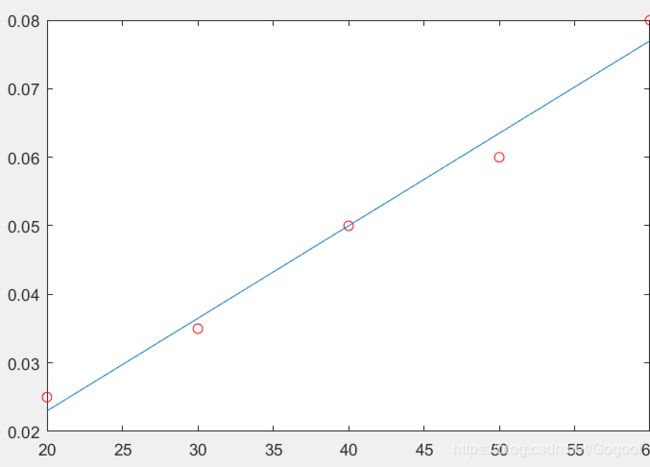
t=[20 30 40 50 60];
c=[0.025 0.035 0.05 0.06 0.08];
fit=polyfit(t,c,1);  %一次函数
y0=polyval(fit,t);   %拟合后直线y值
plot(t,c,'.',t,y0);

ployval(a,x,m) 前者放多项式系数行矩阵，后者放x自变量取值行矩阵 ，m拟合最高次幂。

拟合后的效果：

corrcoef()

相关系数，研究变量之间线性相关程度的量，可在线性拟合前验证线性合适不。

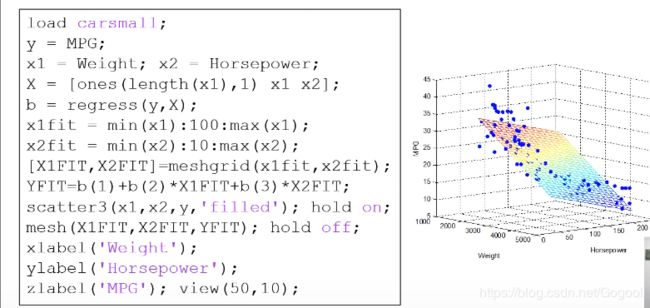
corrcoef(x,y)

regress()—多个变量

当有多个自变量，如三维函数拟合时，不能用polyfit了，用regress具体不多阐述，例子如图所示：

cftool

cftool绝对是好用的办法，可视化界面拟合，提供多种拟合方法。拟合后可生成函数。

如下是个拟合人口增长曲线例子，输入完数据后cftool点击运行即可进入拟合界面。

t=0:11;
people=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0];
cftool

拟合好后，点击generate code生成拟合过程函数，可在函数上修改要求和在其他函数内调用拟合函数，如：

fittedmodel=createFit(t, people);       %调用拟合函数，fittedmodel是个结构体
y = feval(fittedmodel,t)    %计算拟合后的y值

fittedmodel内存有拟合系数，拟合结构和置信度。获取到后可随心处理。如图下所示：

在用的时候只需要点它，如获取系数a：A=fittedmodel.a；

feval计算拟合函数中y的值，类似polyval。

内插

内插与回归教授做了个对比如图，两者有本质上的区别。

回归是利用一个函数拟合整个图形，会有点不在函数上的可能，拟合的是趋势。

内插是两点之间用线连接起来，所有的点都在拟合曲线上，没有一个明确的函数。

 

二维插值

interp1()

yi=interp1(x，y，xi，'method')  

 （x,y）插值节点   eg:x=1:12 y=[5 2 3 ...]  两者的行列必须相同,x必须单调。

xi：被插值点 h=0:0.1:12  分割每隔0.1插一个值

method：‘nearest’  最邻近插值；‘linear’   线性插值； ‘spline’ 三次样条插值； ‘cubic’  立方插值；

Nearest	方法速度最快，占用内存最小，但一般来说误差最大，插值结果最不光滑。
linear	线性插值结果连续，会出现尖顶。
Spline	三次样条插值是所有插值方法中运行耗时最长的，插值函数及其一二阶导函数都连续，是最光滑的插值方法。占用内存比cubic方法小，但是已知数据分布不均匀的时候可能出现异常结果。
Cubic	三次多项式插值法中，插值函数及其一阶导数都是连续的，所以插值结果比较光滑，速度比Spline快，但是占用内存最多。

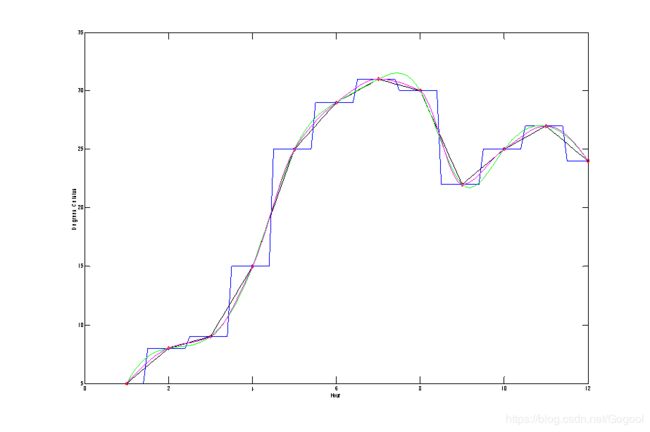
EG:

hours=1:12;
temps=[5 8 9 15 25 29 31 30 22 25 27 24];
h=1:0.1:12;
t1=interp1(hours,temps,h,'nearest');  
t2=interp1(hours,temps,h,'linear');  
t3=interp1(hours,temps,h,'spline');  
t4=interp1(hours,temps,h,'cubic');
plot(hours,temps,'rh',h,t1,'b',h,t2,'k',h,t3,'g', h,t4,'m' )    
xlabel('Hour'),ylabel('Degrees Celsius')

        

三维网格节点数据的插值

interp2()

z=interp2(x0,y0,z0,xii,yii,’method’)  

eg:

x=1:0.5:5;y=1:0.5:3;
z=..;
xi=1:0.2:5;                            xi=linspace(0,5,50);  %加密横坐标数据到50个         
yi=1:0.2:3;                            yi=linspace(0,6,60);  %加密纵坐标数据到60个zi=interp2(x,y,z,xi,yi’,'cubic');      [xii,yii]=meshgrid(xi,yi);  %生成网格数据
%yi逆置！！！                           zii=interp2(x,y,z,xii,yii,'cubic');                   

三维散点数据的插值

griddata()

cz =griddata（x，y，z，cx，cy，‘method’）

小结：整理了片面，还需要后期补充，一些地方理解还不够到位，继续。