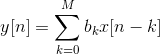FIR的Verilog实现
FIR的Verilog实现
- matlab分析及结果处理:https://github.com/Grootzz/MATLAB-FIR
- Verilog实现:https://github.com/Grootzz/Verilog-FIR
设计总结
- FIR简介
- 用Verilog实现FIR需要注意的问题?
2.1 浮点数和定点数之间的转换
2.2 利用FilterDesigner设计FIR
2.3 Matlab仿真分析
2.4 补码问题 - Verilog实现
- 代码
FIR简介
FIR全称为:Finite Impluse Response,称之为:有限长单位冲击响应滤波器。也叫非递归线性滤波器,也就是抽头没有反馈。显然,这是一种数字域的滤波器。目前实现数字滤波器的方案可分为三种:
- 单片数字滤波器集成电路;
- DSP;
- PLD(可编程逻辑器件)。
一个数字滤波器在离散域常用常系数线性差分方程表示:
其z域的系统函数形式为:
对于FIR来讲,也就是y[n-k]的权值为零(无反馈)。所以FIR的离散域常用常系数线性差分方程为:
系统框图为:
因此,对于一个FIR滤波器,若知道每个抽头的权值和权值个数,则滤波器就可确定下来。
用Verilog实现FIR需要注意的问题?
使用Verilog设计FIR,个人理解最终重要的问题在于输入信号位宽、权值位宽、以及输出信号位宽的确定。它们的确定决定了系统能够处理的信号的范围,而其中涉及到的一个问题就是浮点数转定点数。
至于滤波器阶数以及滤波器抽头权值的确定,可以借用Matlab中的FilterDesigner工具来分析。
2.1 浮点数和定点数之间的转换
浮点数和定点数之间的转换可以理解为两个域之间的转换,浮点域适合域计算机做分析,而定点域适合于具体的硬件实现。那么,计算机开发的算法如何转换成具体的电路实现?这就涉及到一个域的变换的问题。
为了把浮点域中的数据转换成定点域中的数据,可以使用以下步骤:
假设浮点数据为变量a;
-
***step1:**计算b=a 2^(F) ,其中,F的确定至关重要,直接影响了定点域数据的分辨率。注意,b使用十进制表示。
-
***step2:***round;求出b最近的整数值,例如:
round(4.45) = 4;
round(-1.9) = -2;
-
***step3:***将十进制的round(b)用二进制表示,记为c。
-
***step4:***假设c需要n bits可以表示,这n bits包括了定点域的小数部分和整数部分。
上述步骤1中,F的值为如何确定呢?F是十进制a转成二进制时,二进制的小数位数。举例说明:
假设十进制形式的a = 3.625;
那么可以将其二进制形式了可以表示为(1):11.1010;
当然,也可以将其表示为(2):0011.1010;
还可以将其表示为(3):11.10100000;
甚至,还可以将其表示为(4):000011.10100000;
可以看出,这几种二进制的表示方法殊途同归,其值都为十进制3.625;
对于(1),F = 4;
对于(2),F = 4;
对于(3),F = 8;
对于(4),F = 8;
可以看出,F的确定似乎是很随意的,F值越大,能表示的数据越准确;但是,有的浮点数并不能精确地用二进制表示,如:
a = 3.613
这个十进制数用无论多少位二进制都是无法表示的;
加入确定其二进制形式的整数位数为3,小数位数为6,则:
转成二进制数可以为011.100111;
而011.100111实际值为3.609375;
两数之间有0.003625的误差;
可以看出,二进制小数位越多,能表示的浮点数越精确;但实际的硬件电路资源是有限的,不可能针对这种数据不限制地增加小数的位数。
以上就是F的确定,越大越好,但是资源消耗很大;但是太小,影响数据的精度。所以,选取F时,需要在硬件资源和数据精度做一个权衡。
针对浮点转定点,这里给出一个具体的示例:
假设定点数用8位表示,F=3 , a = 3.013;
step1:b = a * 2^(F) = a * 2^(+3) = 24.1040
step2:round(b) = round(24.1040) = 24
step3:c = dec2bin(24) = 11000
step4 : c = 00011.000
step4中的c即为硬件中的定点数形式。
数据操作时用step3中的数据,(因为是定点数据,所以输入11000时,硬件自动划分3位为小数部分,其他的为整数部分)
error = 3.013 - 3 = 0.013
所以,数据位宽的选择很重。当然,这里还有一个问题,也就是数据***溢出***,假设上面的实例中,a = 3.013变为63.013,那整数部分就是111111,显然,5位的整数位宽无法表示这个数据,这就会导致数据溢出。数据溢出存在数据上溢出和数据下溢。
2.2 利用FilterDesigner设计FIR
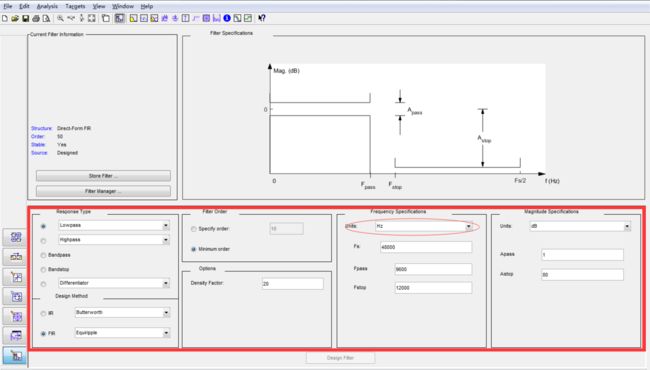
在命令窗口输入filterDesigner;即可打开工具filterDesigner。红色区域设置滤波器具体指标。
值得一提的就是这个采样频率Fs,它是采样信号的频率,就是每秒钟采集多少个点(数据)。
确定设计指标:
- 归一化Fpass = 0.1;通带衰减1dB
- 归一化Fstop = 0.4;阻带衰减80dB
- 采样率Fs = 48000;等纹波
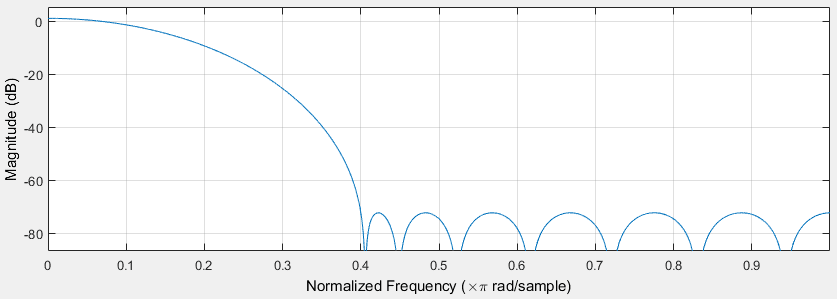
因为归一化频率1对应的频率为Fs/2 , 所以Fpass = 0.1 * Fs/2 ,Fstop = 0.4 * Fs/2 。仿真结果如图为:
设计结果为:
- 结构形式:直接型
- Order:16
- 稳定性:稳定
得出滤波器系数为:
2.3 Matlab仿真分析
Matlab数据分析采用的是浮点型数据分析,而Verilog实现却需要定点数据,所以首先谈一下数据域的转换。
首先确定输入数据的位宽和滤波器抽头系数为16位,输出位宽为32位。确定位宽需要满足两个原则:
- 为定点数据后为8,而位宽却为3,这是不允许的。
- 滤波器内部会涉及到加和乘运算,那么,总的运算要求结果不能溢出。
1) 滤波器系数和输入数据的定点转换
针对抽头系数的定点转换;16位中,除去符号位,若将剩下的15位数全都做位分数位数F , 则数据应该满足以下表达式:
![]()
显然,设计结果中抽头系数满足这个式子。
针对输入数据的定点转换;16位中,除去符号位,还剩下的15位,在本文的设计中,输入数据为:
![]()
其最大值为2,要求数据定点转换后不能溢出。所以定点转换时,定点数据二进制形式的分数位数F选取为14;整数部分用2bits就可表示。则输入数据满足下式:
![]()
2) 滤波器定点装换讨论
因为最后滤波器的输出设置为32位,输入数据和系数均为16位,那么,两个16位数据相乘,最后的结果最多为32位。另外,滤波器中还存在加法运算,那最后的输出数据很可能超出32位。如果不对此作出处理,最后的结果可能溢出,处理的原则为:
![]()
将上面的设计数据带入此式中,有:
![]()
最后的定点数据二进制形式的分数位数F,由1)和2)中较小的值确定。在此例中,仍旧采用15bit的量化数,采用16bit表示滤波器字长(也就是输入数据和系数的位宽)。
3) Round和Truncate
浮点数据乘以2^(F)相当于对浮点数据缩放scaling,scaling后的数据要做round处理,处理后的数据自然地被截断truncate。
4)定点仿真
定点仿真后的一个重要指标,就是数据不能溢出。系统输出为32位,最终的结果要满足:
![]()
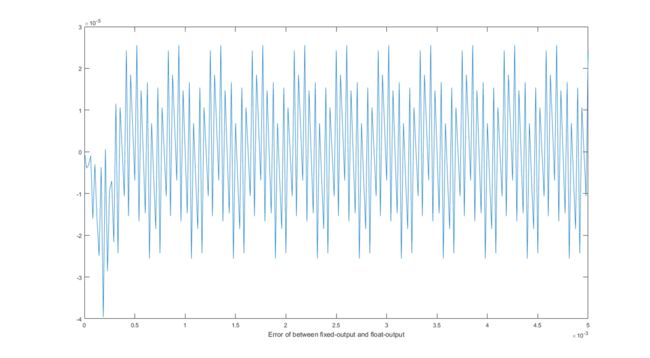
通过Matlab全精度仿真和定点仿真作比较,其结果为:
2.4 补码问题
在用Verilog读取定点抽头系数时,需要将signed数据用补码形式表示,所以,signed整数在做二进制补码的转换时,满足以下公式:
- ###Verilog实现
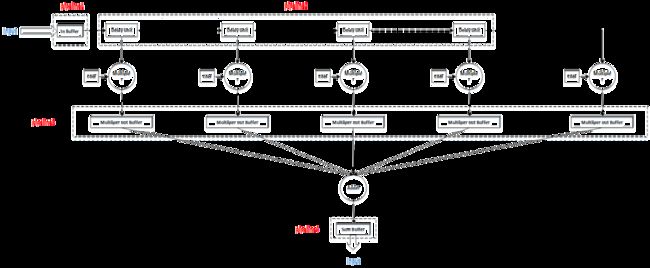
本例设计中,数据输入速率等于FPGA工作频率。整个系统只有一个主时钟。本文采用全并行结构,即多个乘法器同时工作。
模块构成
测试信号由matlab产生,以补码的形式存入databin.mem文件,在testbench中通过$readmemb系统函数读入。
经过FIR后的信号由testbench写入data.txt文件。
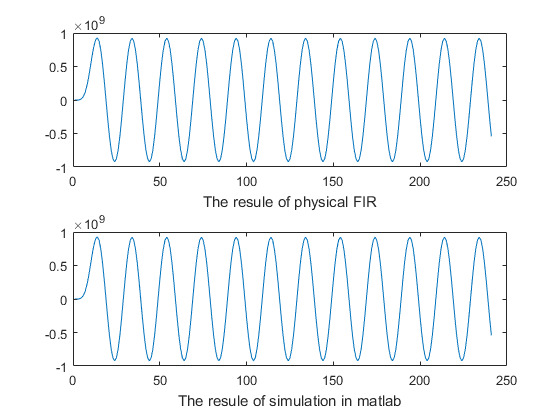
最后利用matlab读取dataout.txt文件,作图比较得出如下结果,误差为0:
- ###代码
1.滤波器分析:浮点域与定点域的分析以及比较
% analysis of floating-point domain and fixed-point for FIR
% FIR coef stem from FilterDesigner tool
% floating-point conversion to fixed-point
clc ,clear, close all;
fs = 48000; % simpling frequency
fpass = 2400;
fstop = 9600;
t = 0:1/fs:0.005; % 0.005 s signal
signal = sin(2*pi*fpass*t) + sin(2*pi*2*fstop*t);
figure(1),subplot(2,1,1);
plot(t , signal);xlabel('signal with noise');
re_signal = filter(LPF , signal);
subplot(2,1,2);
plot(t,re_signal);xlabel('filtered signal without noise');
% floating-point conversion to fixed-point
% filter coefficients
coefStruct = load('coef');
coef = coefStruct.Num;
% define input word length and determined the scaling length
WL = 16;% input word length
IN_SCALE = 14;% input scaling length
COEF_SCALE = 16;% coefficients scaling length
% quantize
signal_scale = round(signal * 2^IN_SCALE);
coef_scale = round(coef * 2^COEF_SCALE);
result_scale = filter(coef_scale , 1 , signal_scale);% filtering signal
err_signal = signal_scale * 2^(-IN_SCALE) - signal;
err_coef = coef_scale * 2^(-COEF_SCALE) - coef;
% de-scale result_scale
result_approximate = result_scale * 2^(-(IN_SCALE + COEF_SCALE));
fprintf('error of scaleing signal and the law singal : %d\n' , sumsqr(result_approximate-re_signal));
figure(2);
subplot(211);plot(t , err_signal); xlabel(['quantized err of signal,','sumsqr:',num2str(sumsqr(err_signal))]);
subplot(212);plot(0:length(coef)-1 , err_coef);xlabel(['quantized err of coef,','sumsqr:',num2str(sumsqr(err_coef))]);
figure(3);
subplot(211);plot(t,signal_scale);xlabel('scaled signal input');
subplot(212);plot(t,result_scale);xlabel('scaled filter output');
figure(4);
plot(t , result_approximate-re_signal);xlabel('Error of between fixed-output and float-output');
f = fopen('databin.txt' , 'w');
fprintf(f ,'%g\n' , signal_scale');
fclose(f);
- 补码运算
% transforminteger number (including positive and negaitive) to Two complement
WIDTH = 16;
signal_trans2c = dec2bin(signal_scale + 2^WIDTH * (signal_scale<0) , WIDTH);
signal_trans2c = signal_trans2c';
fdata = fopen('databin.mem' , 'wb');
for index = 1:length(signal_scale)
for i = 1:WIDTH
fprintf( fdata ,'%s' , signal_trans2c((index-1) * WIDTH + i));
end
fprintf(fdata , '\r\n'); % entering a enter and new a line
end
fclose(fdata);
- 定点域内,物理实现的滤波器和matlab分析的滤波器输出的比较。
% read data solved by physical FIR
% dataout.txt is the read object
fid = fopen('E:\ISEProjece\FirDesign\dataout.txt');
fpga_data = textscan(fid, '%d');
fclose(fid);
subplot(211);
% begin output is 0 ,because use 5-level pipeline in physical FIR
plot(fpga_data{1}(6:end));xlabel('The resule of physical FIR');
subplot(212);
plot(result_scale);xlabel('The resule of simulation in matlab');
fprintf('eror (sum of squared) between simulation and physical fir is : %d \n' , sumsqr(double(fpga_data{1}(6:end)) - result_scale'));
- FIR的Verilog实现
`timescale 1ns / 1ps
//////////////////////////////////////////////////////////////////////////////////
// Company:
// Engineer: anxu chan
//
// Create Date: 16:17:14 08/02/2017
// Design Name: FIR filter
// Module Name: fir
// Project Name: FirDesign
// Target Devices: Xilinix V5
// Description: fir res file
// Revision: 1.0
// Revision 0.01 - File Created
// Additional Comments:
//
//////////////////////////////////////////////////////////////////////////////////
module fir(
input clk,
input rst,
input wire signed [15:0] filter_in,
output reg signed [31:0] filter_out
);
parameter word_width = 16;
parameter order = 16;
// define delay unit , input width is 16 , filter order is 16
reg signed [word_width-1:0] delay_pipeline[order:0];
// define coef
wire signed [word_width-1:0] coef[order:0];
assign coef[0] = -17;
assign coef[1] = 62;
assign coef[2] = 456;
assign coef[3] = 1482;
assign coef[4] = 3367;
assign coef[5] = 6013;
assign coef[6] = 8880;
assign coef[7] = 11129;
assign coef[8] = 11983;
assign coef[9] = 11129;
assign coef[10] = 8880;
assign coef[11] = 6013;
assign coef[12] = 3367;
assign coef[13] = 1482;
assign coef[14] = 456;
assign coef[15] = 62;
assign coef[16] = -17;
// define multipler
reg signed [31:0] product[16:0];
// define sum buffer
reg signed [31:0] sum_buf;
// define input data buffer
reg signed [15:0] data_in_buf;
// data buffer
always @(posedge clk or negedge rst) begin
if (!rst) begin
data_in_buf <= 0;
end
else begin
data_in_buf <= filter_in;
end
end
// delay units pipeline
always @(posedge clk or negedge rst) begin
if (!rst) begin
delay_pipeline[0] <= 0 ;
delay_pipeline[1] <= 0 ;
delay_pipeline[2] <= 0 ;
delay_pipeline[3] <= 0 ;
delay_pipeline[4] <= 0 ;
delay_pipeline[5] <= 0 ;
delay_pipeline[6] <= 0 ;
delay_pipeline[7] <= 0 ;
delay_pipeline[8] <= 0 ;
delay_pipeline[9] <= 0 ;
delay_pipeline[10] <= 0 ;
delay_pipeline[11] <= 0 ;
delay_pipeline[12] <= 0 ;
delay_pipeline[13] <= 0 ;
delay_pipeline[14] <= 0 ;
delay_pipeline[15] <= 0 ;
delay_pipeline[16] <= 0 ;
end
else begin
delay_pipeline[0] <= data_in_buf ;
delay_pipeline[1] <= delay_pipeline[0] ;
delay_pipeline[2] <= delay_pipeline[1] ;
delay_pipeline[3] <= delay_pipeline[2] ;
delay_pipeline[4] <= delay_pipeline[3] ;
delay_pipeline[5] <= delay_pipeline[4] ;
delay_pipeline[6] <= delay_pipeline[5] ;
delay_pipeline[7] <= delay_pipeline[6] ;
delay_pipeline[8] <= delay_pipeline[7] ;
delay_pipeline[9] <= delay_pipeline[8] ;
delay_pipeline[10] <= delay_pipeline[9] ;
delay_pipeline[11] <= delay_pipeline[10] ;
delay_pipeline[12] <= delay_pipeline[11] ;
delay_pipeline[13] <= delay_pipeline[12] ;
delay_pipeline[14] <= delay_pipeline[13] ;
delay_pipeline[15] <= delay_pipeline[14] ;
delay_pipeline[16] <= delay_pipeline[15] ;
end
end
// implement product with coef
always @(posedge clk or negedge rst) begin
if (!rst) begin
product[0] <= 0;
product[1] <= 0;
product[2] <= 0;
product[3] <= 0;
product[4] <= 0;
product[5] <= 0;
product[6] <= 0;
product[7] <= 0;
product[8] <= 0;
product[9] <= 0;
product[10] <= 0;
product[11] <= 0;
product[12] <= 0;
product[13] <= 0;
product[14] <= 0;
product[15] <= 0;
product[16] <= 0;
end
else begin
product[0] <= coef[0] * delay_pipeline[0];
product[1] <= coef[1] * delay_pipeline[1];
product[2] <= coef[2] * delay_pipeline[2];
product[3] <= coef[3] * delay_pipeline[3];
product[4] <= coef[4] * delay_pipeline[4];
product[5] <= coef[5] * delay_pipeline[5];
product[6] <= coef[6] * delay_pipeline[6];
product[7] <= coef[7] * delay_pipeline[7];
product[8] <= coef[8] * delay_pipeline[8];
product[9] <= coef[9] * delay_pipeline[9];
product[10] <= coef[10] * delay_pipeline[10];
product[11] <= coef[11] * delay_pipeline[11];
product[12] <= coef[12] * delay_pipeline[12];
product[13] <= coef[13] * delay_pipeline[13];
product[14] <= coef[14] * delay_pipeline[14];
product[15] <= coef[15] * delay_pipeline[15];
product[16] <= coef[16] * delay_pipeline[16];
end
end
// accumulation
always @(posedge clk or negedge rst) begin
if (!rst) begin
sum_buf <= 0;
end
else begin
sum_buf <= product[0] + product[1]+ product[2]+ product[3]+ product[4]
+ product[5]+ product[6]+ product[7]+ product[8]+ product[9]+ product[10]
+ product[11]+ product[12]+ product[13]+ product[14]+ product[15]+ product[16];
end
end
always @(sum_buf) begin
if (!rst) begin
filter_out = 0;
end
else begin
filter_out = sum_buf;
end
end
endmodule
- testbench文件
`timescale 1ns / 1ps
////////////////////////////////////////////////////////////////////////////////
// Company:
// Engineer: anxu chan
//
// Create Date: 16:17:14 08/02/2017
// Design Name: FIR filter
// Module Name: fir
// Project Name: FirDesign
// Target Devices: Xilinix V5
// Description: test bench
// Revision: 1.0
// Revision 0.01 - File Created
// Additional Comments:
//
////////////////////////////////////////////////////////////////////////////////
module fir_tb;
// Inputs
reg clk;
reg rst;
reg signed [15:0] filter_in;
// Outputs
wire signed [31:0] filter_out;
// Instantiate the Unit Under Test (UUT)
fir uut (
.clk(clk),
.rst(rst),
.filter_in(filter_in),
.filter_out(filter_out)
);
// define reset time
initial begin
rst = 0;
#15;
rst = 1;
end
// define clock
initial begin
clk = 0;
forever #10 clk = ~clk;
end
// define a ram store input signal
reg signed[15:0] mem[241:0];
// read data from disk
initial begin
$readmemb("E:/MatlabProject/databin.mem" , mem);
end
// send data to filter
integer i=0;
initial begin
#15;
for(i = 0 ; i < 242 ; i = i+1) begin
filter_in = mem[i];
#20;
end
end
// write data to txt File
integer file;
integer cnt=0;
initial begin
file = $fopen("dataout1.txt" , "w");
end
// write data was filtered by fir to txt file
always @(posedge clk) begin
$fdisplay(file , filter_out);
end
always @(posedge clk) begin
$display("data out (%d)------> : %d ," , cnt, filter_out);
cnt = cnt + 1;
if (cnt == 250) begin
#20 $fclose(file);
rst = 0;
#20 $stop;
end
end
endmodule
#####实现思路巩固
代码托管Github:
- matlab分析及结果处理:https://github.com/Grootzz/MATLAB-FIR
- Verilog实现:https://github.com/Grootzz/Verilog-FIR