GAN的优化（一）：生成模型与GAN

本文首发于微信公众号：有三AI
今天是第一期，在正式进入GAN之前，我们有必要先介绍一些GAN的背景知识，理一理各种生成模型的那些千丝万缕的联系，然后深入到GAN中去。

1.生成模型

在机器学习或者深度学习领域，生成模型具有非常广泛的应用，它可以用于测试模型的高维概率分布的表达能力，可以用于强化学习、半监督学习，可以用于处理多模输出问题，以及最常见的产生“真实”数据问题。

我们有必要先说明一个问题，本专栏所讲述的GAN包括VAE、玻尔兹曼机等其他生成模型均属于无监督学习的范畴，这与李航老师的《统计学习方法（第一版）》里的有监督学习生成方法有所区别。简单而言，有监督学习与无监督学习的区别之处在于是否存在标签信息。在有监督学习生成方法中，我们学得联合概率分布P(X,Y)，然后求出生成模型P(Y|X)，其重点在于学习联合分布。例如，在朴素贝叶斯方法中，我们通过数据集学习到先验概率分布P(Y)和条件概率分布P(X|Y)，即可得到联合概率分布P(X,Y)；在隐马尔可夫模型中，我们通过数据集学习到初始概率分布、状态转移概率矩阵和观测概率矩阵，即得到了一个可以表示状态序列和观测序列的联合分布的马尔可夫模型。而在GAN、VAE等无监督生成模型中，只存在关于X的数据集，我们的目标或者近似得到P(X)的概率密度函数，或者直接产生符合X本质分布的样本。

2.极大似然估计

我们从最简单的生成模型开始说起。考虑这样一个问题，依概率P(X)在X中独立采样n次构建一个包含n样本的数据集，如何根据这个数据集来求得X的概率密度函数P(X)。其实这个问题并不容易解决，可是如果再额外提供一些关于X的先验知识，比如X服从正态分布，那这个问题便可以使用极大似然法轻松搞定。

如若X服从正态分布，则概率密度函数P(X)的表达式形式已知，只需要再确定均值、方差两个参数值便可以得到P(X)。接下来便是计算数据集的似然函数，对似然函数取负对数，然后最小化即可，即$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmin}}-\sum _{i=1}^{m}logp(x_i;\theta )$$其实，对随机变量X的概率密度函数的建模源于先验知识，极大似然估计只是一个参数估计的方法。容易证明，极大似然法本质上是在最小化数据集的经验性分布和模型分布之间的KL散度，而且当具备某些条件时，参数的极大似然估计值会趋近于真实值。

3.显式的概率密度函数

当不知道X的概率密度函数P(X)的表达形式，或者该表达式极其复杂的时候，我们如何对P(X)建模？这时，借用神经网络强大的函数拟合能力、表达能力，我们可以用来拟合相关函数来显式地构造P(X)。
例如在自回归网络中，我们将d维随机变量X的联合概率分布通过链式法则进行分解，$$p(x)=\prod _{i=1}^{n}p(x_i\mid x_1,x_2,...,x_{i-1})$$其中的条件概率分布由神经网络进行表示。

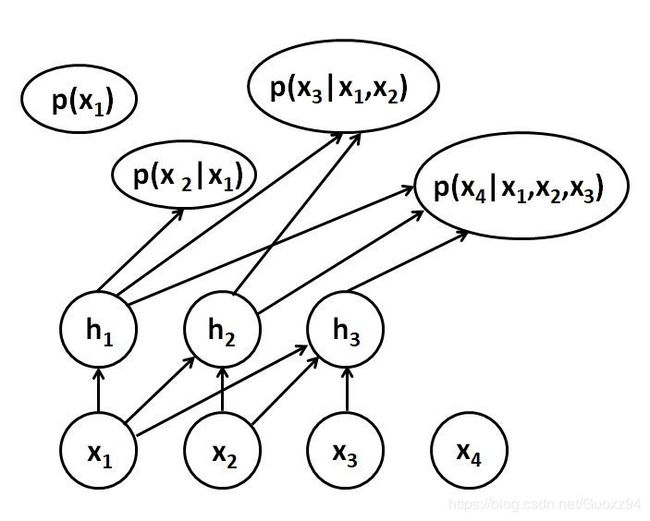
另一类是以深度信念网络、深度玻尔兹曼机以及各种变体为代表的通过加入隐变量来建模P(X)的方法。它们的结构分为可见层和隐层，可见层用于接受输入，隐层单元用于特征表示。隐变量类似于多层感知器中的隐藏单元，用来模拟可见层的高阶交互，可提高网络的表达、拟合能力。训练目标均是使可见层节点的分布最大可能接近样本的真实分布。其区别之处在于深度玻尔兹曼机是一个完全无向模型，而深度信念网络的是有向图和无向图的混合模型，是受限玻尔兹曼机的堆叠。


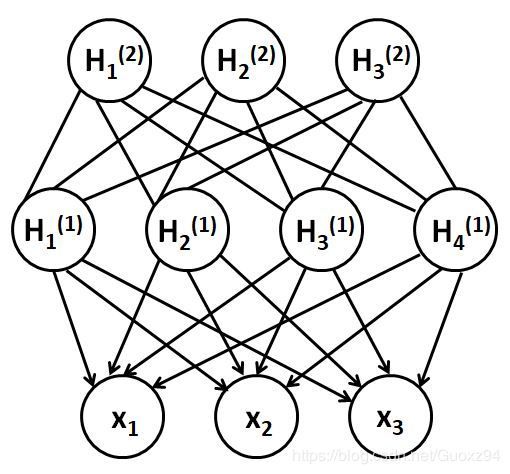
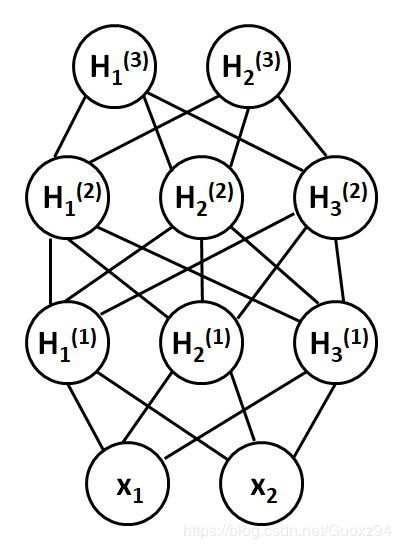
以深度玻尔兹曼机为例，使用能量函数定义联合概率分布，其中Z为朴素的归一化配分函数。
我们仍然可以使用极大似然法进行训练，但是需要解决两个困难的计算问题，一个是边缘化隐变量时的推断问题，一个是配分函数的梯度求解问题。
再一种是基于可微生成器网络，使用可微函数g(z)将隐变量z的样本变换为样本x上的分布。其典型代表便是VAE，其将x显式建模为$$p(x\mid z)$$VAE中也需要使用变分法近似最大似然函数。
无论如何显式地定义概率密度函数P(X)，其基本思路都是极大化样本集的似然函数，最终求解出P(X)中的参数，某些模型需要加一个边缘化隐变量的操作。在自回归网络中，计算难度不算太大，但是在深度玻耳兹曼机、深度信念网络中涉及到图模型和隐变量时，不可避免要使用马尔可夫链近似、变分推断等技术。

4.GAN

再思考一个问题，依概率P(X)在X中独立采样n次构建一个包含n样本的数据集，如何根据这个数据集来训练一个模型，使得模型能源源不断产生符合X概率分布的样本？
如若只是产生样本，生成模型不必非要去显式定义概率密度函数，然后近似求解P(X)，就比如在深度玻尔兹曼机中，不仅训练时运算复杂，采样产生样本时还需要Gibbs采样技术。
还是在可微生成器网络中，不同于VAE，我们使用可微函数g(z)将潜变量z变化为样本x，全程没有任何显式地出现过概率密度函数，直接做一个end-to-end的模型。g(z)的本质是一个参数化计算过程，它能很好地学习到z排布情况以及从z到x的映射。我们所做的就是根据训练数据来推断参数，然后选择合适的g，其代表便是GAN。
GAN（对抗生成网络）是一种深度生成模型，由Gooldfellow于2014年首次提出，现已发展成时下最火热的模型之一。其设计灵感来自于博弈论，一般由生成器和判别器两个神经网络构成，通过对抗方式进行训练，最后得到一个性能优异的生成器。

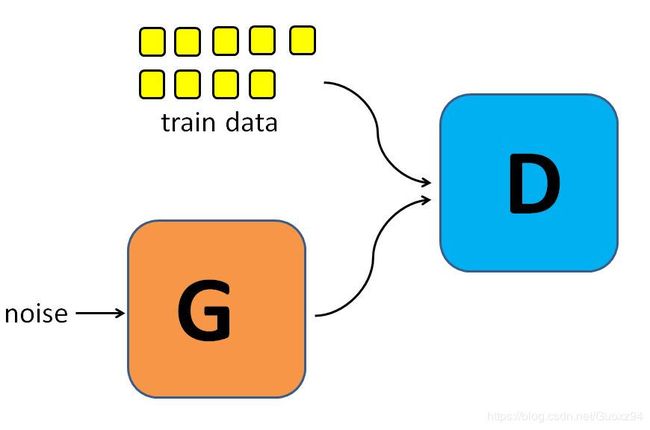
GAN的核心任务是：使生成器G产生的样本的概率分布尽量接近训练集的概率分布。判别器D的功能类似于逻辑回归，对于一个样本x,判别器D(x)将给出该样本来源于训练集的概率，所以一个“完美”的判别器应该对来自于训练集的样本输出概率1，对来自于生成器的生成样本输出概率0；对于生成器G，它试图捕捉到训练集的本质模式，生成样本并将样本送至判别器D，最好能使该样本“欺骗”判别器，使判别器误认为该样本来源于训练集而输出概率1。通过这个对抗生成过程，GAN没有显式地建模P(x)，也可以得到满足P(x)分布的样本。

4.1 判别器

训练判别器，就是在做类似于有监督学习中的逻辑回归的问题。用于训练的样本包括两部分，原始训练集（其标签为1）、生成样本集（其标签为0），还是使用极大似然方法便可以得到其目标函数。
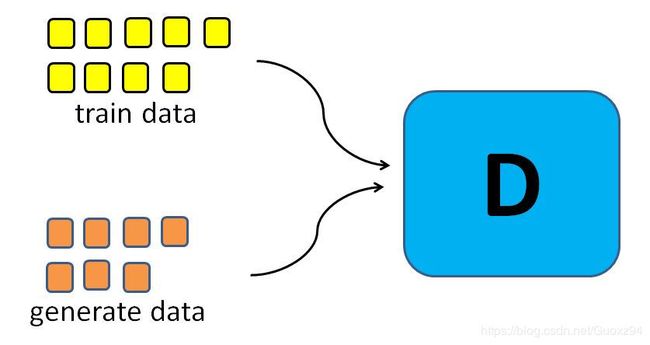现在我们将从极大似然出发，构建判别器的目标函数。
对于任意样本$x$，其似然函数为
$$[D_w(x){]}^y[1-D_w(x){]}^{(1-y)}$$则总似然函数为
$$\prod _{i=1}^{n_1}[D_w(x_{data}^i)]\prod _{j=1}^{n_2}[1-D_w(x_g^j)]$$取对数为
$$\begin{array}{rl}& log\{\prod _{i=1}^{n_1}[D_w(x_{data}^i)]\prod _{j=1}^{n_2}[1-D_w(x_g^j)]\}\\ =& \sum _{i=1}^{n_1}log[D_w(x_{data}^i)]+\sum _{j=1}^{n_2}log[1-D_w(x_g^j)]\end{array}$$将总似然函数最大化即可得到目标函数
$$\begin{array}{rl}& \underset{w}{\max }\{\sum _{i=1}^{n_1}log[D_w(x_{data}^i)]+\sum _{j=1}^{n_2}log[1-D_w(x_g^j)]\}\\ \iff & \underset{w}{\max }{\mathbb{E}}_{x\sim p_{data}}log[D_w(x)]+{\mathbb{E}}_{x\sim p_g}log[1-D_w(x)]\end{array}$$现在，得到了目标函数，我们来看看最佳判别器的数学形式。对目标函数求梯度并使其为0，有
$$\begin{array}{rl}& \frac{\partial \{{\mathbb{E}}_{x\sim p_{data}}log[D_w(x)]+{\mathbb{E}}_{x\sim p_g}log[1-D_w(x)]\}}{\partial w}=0\\ \iff & \frac{\partial \{{\int }_x{p}_{data}(x)log[D_w(x)]dx+{\int }_x{p}_g(x)log[1-D_w(x)]dx\}}{\partial w}=0\\ \iff & \frac{\partial \{{\int }_x{p}_{data}(x)log[D_w(x)]+p_g(x)log[1-D_w(x)]dx\}}{\partial w}=0\\ \iff & {\int }_x\frac{\partial \{p_{data}(x)log[D_w(x)]+p_g(x)log[1-D_w(x)]\}}{\partial w}dx=0\\ \iff & {\int }_x\frac{\partial \{p_{data}(x)log[D_w(x)]+p_g(x)log[1-D_w(x)]\}}{\partial D_w(x)}\frac{\partial D_w(x)}{\partial w}dx=0\\ \iff & \frac{\partial \{p_{data}(x)log[D_w(x)]+p_g(x)log[1-D_w(x)]\}}{\partial D_w(x)}=0\\ \iff & D^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\end{array}$$认真琢磨一下这个式子，理想状态下的最优判别器还是非常“简单而务实”的。当$p_g(x)=p_{data}(x)$时，判别器将无法做出任何有效判断，对任何样本$x$，均有$D(x)=0.5$。

4.2 生成器

论文最开始提出的生成器也是全连接网络，它不断优化，使产生的样本尽量欺骗判别器（即判别器输出尽量大）。

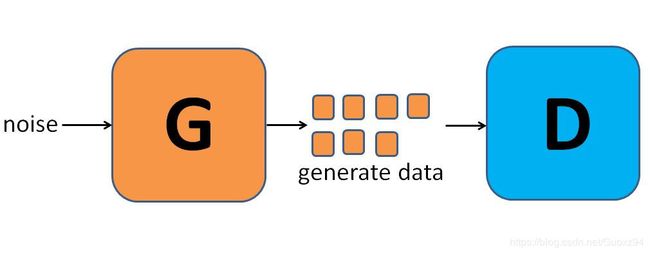
我们来看一下，生成器的目标函数到底是什么。将最优判别器代入，可有
$$\begin{array}{rl}& \underset{w}{\min }{\mathbb{E}}_{x\sim p_{data}}log[D^{\ast }(x)]+{\mathbb{E}}_{z\sim p_z}log[1-D^{\ast }(G_w(z))]\\ =& \min {\mathbb{E}}_{x\sim p_{data}}log[D^{\ast }(x)]+{\mathbb{E}}_{x\sim p_g}log[1-D^{\ast }(x)]\\ =& \min {\mathbb{E}}_{x\sim p_{data}}\left[log\frac{p_{data}(x)}{\frac{p_{data}(x)+p_g(x)}{2}}\right]-log4\\ & +{\mathbb{E}}_{x\sim p_g}\left[log\frac{p_g(x)}{\frac{p_{data}(x)+p_g(x)}{2}}\right]\\ =& \min D_{KL}(p_{data}(x)\parallel \frac{p_{data}(x)+p_g(x)}{2})-log4\\ & +D_{KL}(p_g(x)\parallel \frac{p_{data}(x)+p_g(x)}{2})\\ =& \min 2D_{JS}\left(p_{data}(x)\parallel p_g(x)\right)-log4\end{array}$$其实发现，$G_w(x)$是在JS散度作为目标函数的指示下不断增强自己的生成能力，理论上最好的结果是$JS\left(p_{data}(x)\parallel p_g(x)\right)=0$，此时$G_w(x)$最优。
其实真正在指导生成器进行训练的是隐式定义的分布和数据集真实分布的JS散度。当两个分布完全重合时，生成器的目标函数值达到最小-lg4，且此时的判别器也为最优，对任意输入，均给出D(x)=0.5。理论上可证明，只要有足够的精度，模型一定能收敛到最优解。
另外，在训练生成器时，可使用另一个目标函数trick，我们来看看这个目标函数的本质。
$$\underset{w}{\min }-{\mathbb{E}}_{z\sim p_z}logD(G_w(z))$$我们现在看看这个目标函数本质是什么？如果把最优判别器代入，有
$$\begin{array}{rl}& \underset{w}{\min }-{\mathbb{E}}_{z\sim p_z}logD(G_w(z))\\ =& \min -{\mathbb{E}}_{x\sim p_g}log{D}^{\ast }(x)\\ =& \min -{\mathbb{E}}_{x\sim p_g}log\left[\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\right]\\ =& \min -{\mathbb{E}}_{x\sim p_g}log\left[\frac{p_g(x)}{p_{data}(x)+p_g(x)}\right]+{\mathbb{E}}_{x\sim p_g}log\left[\frac{p_g(x)}{p_{data}(x)}\right]\\ =& \min {\mathbb{E}}_{x\sim p_{data}}\left[log\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\right]+D_{KL}(p_g\parallel p_{data})\\ & -2D_{JS}\left(p_{data}(x)\parallel p_g(x)\right)+log4\\ =& \min {\mathbb{E}}_{x\sim p_{data}}\left[log{D}^{\ast }(x)\right]+D_{KL}(p_g\parallel p_{data})\\ & -2D_{JS}\left(p_{data}(x)\parallel p_g(x)\right)+log4\\ \iff & \min D_{KL}(p_g\parallel p_{data})-2D_{JS}\left(p_{data}(x)\parallel p_g(x)\right)\end{array}$$单纯从数学的角度来看，这个目标函数是自相矛盾的，最大JS散度的同时减少KL散度，这样的训练可以认为是没有什么意义的。

4.总结

现在我们已经有两个来看待GAN的角度了，从博弈论的角度，先学得一个好的判别器，它能准确分辨出样本的来源，然后让生成器尽量取“欺骗”判别器，达到“安能辨我是雌雄”的境界。但是从纯数学的角度来看这套框架，则是先最优化判别器，此时便学习到了$p_g$和$p_{data}$的差异度量—JS散度，然后以JS散度为目标函数指导生成器进行学习，当最后JS散度为0时，$p_g$和$p_{data}$重合。
同时，作者也证明了只要生成器和判别器拥有足够的精度，$p_g$最终将收敛到$p_{data}$。这套框架在理论上看起来无懈可击，但是实际中也存在诸多问题，比如JS散度的梯度消失，样本多样性差的问题，这些问题之后将会解释。