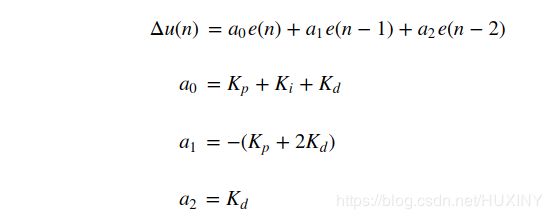模糊pid算法实现(Java)
参考文章:
https://blog.csdn.net/shuoyueqishilove/article/details/78236541
https://blog.csdn.net/qq_41913616/article/details/82020685
https://www.cnblogs.com/foxclever/p/9940253.html
1 简介
模糊pid属于智能算法的一种,智能算法也可以叫非模型算法,也就是说,当我们无法确定系统模型时智能算法常常能够起到不小的作用。在现实世界中,大多数系统系统都是非线性的,不可预测的。
智能算法包括专家系统,模糊算法,遗传算法,神经网络算法等。其中任何一种算法都可以跟PID去做结合,而选择的关键在于,处理的实时性能不能得到满足。
模糊算法其实并不模糊,模糊算法其实也是逐次求精的过程。模糊算法的原理实际上是模仿人对系统进行调节的过程,以温度控制系统来说明,预设温度与现温度的偏差即温度误差较大时,控制器会加大火力;温度误差较小时,控制器会减小火力。模糊算法的关键就在于如何描述当前误差是大还是小,如何根据误差的大小决定系统的控制策略。
我们的目的是结合模糊算法在控制过程中动态改变PID过程的三个重要参数,从而使控制更精确和稳定。
2 模糊pid算法流程
3 模糊PID的实现
模糊pid其实就是在普通pid的基础上,通过输入的两个变量:误差和误差的变化率的情况来动态调整pid控制器的三个重要参数kp,ki,kd。从而使控制器的性能达到最优。这里的pid参数整定,使用的是增量的方式,这样可以避免过大的误差,提高整定的精度。
所使用的模糊控制器的设计方法与普通的模糊控制器设计是一样的,具体为:首先确定模糊控制器的输入为二维输入(可以设计成多维的),即误差和误差的变化率作为模糊控制器的输入;模糊控制器的输出为PID参数的增量值,分别为△kp,△ki,△kd;
则PID的参数为:
Kp(n) = Kp(n-1) + △kp
Ki(n) = Ki(n-1) + △ki
Kd(n) = Kd(n-1) + △kd
3.1 模糊化
输入值量化
输入值的模糊化就是将用于计算的输入映射到标准化的数值区间,并根据量化结果和模糊化子集得到该输入对子集的隶属度。我们使用偏差e和偏差增量△e作为输入实现控制参数调整,则需要对e和△e进行模糊化。
首先,我们确定e和△e的模糊子集,对于PID控制我们选择:负大[NB]、负中[NM]、负小[NS]、零[ZO]、正小[PS]、正中[PM]、正大[PB] 7 个语言变量就能够有足够的精度表达其模糊子集。所以,我们定义e和△e的模糊子集均为{NB、NM、NS、ZO、PS、PM、PB}。
确定了模糊子集,我们怎么将e和△e的具体值和模糊集对应上呢?我们需要引入量化函数。要确定量化函数,我们需要先引入e和△e模糊集对应的论域,定义为{-3, -2, -1, 0, 1, 2, 3}。这里我们采用线性的方式量化,量化公式如下:
f(e) = 3e / e_max f(de) = 3de / de_max
解释:
- 1.为什么要乘上3 ?
因为e和de映射到的区间是[3, -3] - 2.e_max和de_max是什么?
e_max是e的最大偏差, 人为设定的值,认为e的范围是[-e_max, e_max],且将[-e_max, e_max]映射到[-3, 3]上;
de_max同理
确定隶属度
利用上述的量化函数就可以将e和△e量化,量化后还要计算e和△在模糊子集上的隶属度。隶属度是一个介于0和1之间的值,用以描述对应一个输入属于某一个模糊子集的程度。一般我们描述成隶属函数,可采用的隶属函数与很多,我们这里采用线性隶属函数,或称为三角隶属函数,其函数关系如下:

如果我们量化后的结果是0.5,那么属于ZO的隶属度为0.5,属于PS的隶属度也是0.5,属于其他的隶属度为0。
至此模糊化全部完成。
3.2 建立模糊规则表
前面我们简述了输入的模糊化,但模糊推理才是模糊控制的根本。为了实现模糊推理首先我们需要建立模糊推理规则库或称为知识库,然后建立推理机进行推理。
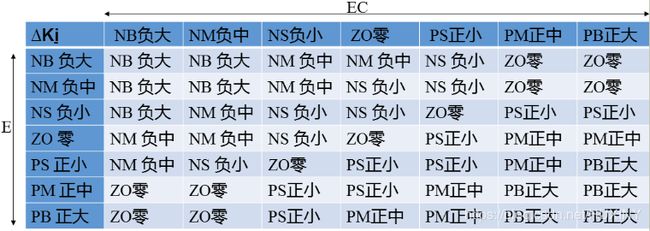
首先,我们来建立模糊规则库,模糊算法最是要对Kp、Ki、Kd三个参数进行调整,所以要建立这3个变量的模糊规则库。
(下面的PID模糊规则表是根据前人的大量研究而设计的,我们直接使用即可)
(1) . Kp模糊规则设计
在pid控制器中,Kp值的选取决定于系统的响应速度,增大Kp能提高响应速度,减小稳态误差,但是Kp值过大会产生较大的超调,甚至使系统不稳定;减小Kp可以减小超调,提高稳定性,但Kp过小会减缓系统的响应速度,延长调节时间。因此,调节初期应适当取较大的Kp值以提高响应速度,而在调节中期,Kp则取较小值,以使系统具有较小的超调并保证一定的响应速度;而在调节的后期将Kp到较大的值来减小静态误差,提高控制精度。
基于上述描述设计出来的Kp模糊规则表如下:
(2) . Ki模糊规则设计
在系统控制中,积分控制主要是用来消除系统的稳态误差的。由于某些原因,积分过程有可能在调节过程的初期产生积分饱和,从而引起调节过程中的较大超调。因此,在调节过程的初期,防止积分饱和,其积分作用应该弱一些,甚至可以取0零;而在调节的中期,为了避免影响稳定性,其积分作用应该比较适中;最后在调节后期,则应该加强积分作用,较小静态误差。
(3) . Kd模糊规则设计
微分环节的调整是针对大惯性过程引入的,微分环节系数的作用在于改变系统的动态特性。系统的微分环节系数能反映型号变化的趋势,并能在偏差信号变化太大之前,在系统中引入一个有效的早期修正信号,从而加快响应速度,减少调整时间,消除震荡,最终改变系统的动态性能。因此,Kd值的选取对调节动态特性的影响很大。Kd值过大,调节过程的制动就会超前,致使调节时间过长;Kd值过小,调节制动就会落后,从而导致超调增加。根据实际过程经验,在调节初期,应增大微分作用,这样可以得到减小甚至避免超调;而在中期,由于调节特性对Kd值的变化比较敏感,因此,Kd值应适当小一些并保证固定不变;然后在调节后期,Kd值应减小,以减小被控制过程的制动作用,进而补偿在调节过程初期由于Kd过大所造成的调节过程时间延长。
基于上述描述设计出来的Ki模糊规则表如下:
接下来,根据偏差E和偏差增量△E模糊化的结果以及规则库推理出△Kp、△Ki、△Kd对应的模糊子集。由于前面我们设计的上采用隶属函数来定义输入输出量在模糊子集的隶属度,所以推理出来的△Kp、△Ki、△Kd的模糊子集通常是由一个模糊变量组成的矩阵。而输入量E和△E则是一个由模糊变量组成的向量。
3.3 解模糊处理
对于求得的目标对象,我们还需要将其解模糊处理以使其与具体的物理量相对应。在模糊PID调解中,我们需要的是Kp,Ki和Kd,所以我们需要根据模糊推理的结果得到我们想要的Kp,Ki和Kd值。
我们前面设计了三角隶属函数,并采用相同的量化目标(即论域)[-3, 3], 所以在某一时刻,输入输出所处的模糊变量的隶属度是相同的,基于这一基础,我们采用重心法计算各输出量的量化值。
公式如下:

得到增量后,我们也可以引入系数来放大和缩小△Kp,△Ki和△Kd,具体实现公式如下:
![]()
注意:
其中,△K为我们所计算得到的值,而α为系数,设定增量对最终结果的影响;
一般的我们会设置一个deltaKp_max, 希望得到的结果在[-deltaKp_max, deltaKp_max]上,然而解模糊后的△K在[-3, 3]上,所以这里的α = deltaKp_max / 3 。
代码实现
该代码是参照网上C代码移植到Java的,并对其进行了修正:
结合文章和代码注释,很容易理解
public class FuzzyPID {
public static int N = 7;
private float target; // 控制目标
private float actual; // 采样获得的真实值
private float e; // 误差
private float e_pre_1;
private float e_pre_2;
private float de;
private float emax; // 误差基本论域上限 ///
private float demax; // 误差变化基本率论域上限 ///
private float delta_Kp_max; // delta_kp输出上限
private float delta_Ki_max;
private float delta_Kd_max;
private float Ke; // 用于将e映射到论域[-3,3]上
private float Kde; // 用于将de映射到论域[-3,3]上
private float Ku_p; // 用于将△Kp结果映射到[-delta_Kp_max, delta_Kp_max]上
private float Ku_i; // 同理
private float Ku_d;
private int[][] Kp_rule_matrix = new int[N][N]; // Kp模糊规则矩阵
private int[][] Ki_rule_matrix = new int[N][N]; // Ki模糊规则矩阵
private int[][] Kd_rule_matrix = new int[N][N]; // Kd模糊规则矩阵
private String mf_t_e; // e的隶属函数类型
private String mf_t_de; // de的隶属函数类型
private String mf_t_Kp; // kp的隶属函数类型
private String mf_t_Ki; // ki的隶属函数类型
private String mf_t_Kd; // kd的隶属函数类型
private float[] e_mf_paras; // 误差的隶属函数的参数
private float[] de_mf_paras;
private float[] Kp_mf_paras;
private float[] Ki_mf_paras;
private float[] Kd_mf_paras;
private float Kp;
private float Ki;
private float Kd;
private float A;
private float B;
private float C;
FuzzyPID(float e_max, float de_max, float kp_max, float ki_max, float kd_max, float Kp0, float Ki0, float Kd0){
target = 0;
actual = 0;
emax = e_max;
demax = de_max;
delta_Kp_max = kp_max;
delta_Ki_max = ki_max;
delta_Kd_max = kd_max;
e_mf_paras = null;
de_mf_paras = null;
Kp_mf_paras = null;
Ki_mf_paras = null;
Kd_mf_paras = null;
e = target - actual;
e_pre_1 = 0;
e_pre_2 = 0;
de = e - e_pre_1;
Ke = (N/2)/emax; ///
Kde = (N/2)/demax;
Ku_p = delta_Kp_max/(N/2); ///
Ku_i = delta_Ki_max/(N/2);
Ku_d = delta_Kd_max/(N/2);
mf_t_e = "No type";
mf_t_de = "No type";
mf_t_Kp = "No type";
mf_t_Ki = "No type";
mf_t_Kd = "No type";
Kp = Kp0;
Ki = Ki0;
Kd = Kd0;
A = Kp+Ki+Kd;
B = -2*Kd - Kp;
C = Kd;
}
FuzzyPID(float[] fuzzyLimit, float[] pidInitVal){
target = 0;
actual = 0;
e = 0;
e_pre_1 = 0;
e_pre_2 = 0;
de = e-e_pre_1;
emax = fuzzyLimit[0];
demax = fuzzyLimit[1];
delta_Kp_max = fuzzyLimit[2];
delta_Ki_max = fuzzyLimit[3];
delta_Kd_max = fuzzyLimit[4];
Ke = (N/2)/emax;
Kde = (N/2)/demax;
Ku_p = delta_Kp_max/(N/2);
Ku_i = delta_Ki_max/(N/2);
Ku_d = delta_Kd_max/(N/2);
mf_t_e = "No type";
mf_t_de = "No type";
mf_t_Kp = "No type";
mf_t_Ki = "No type";
mf_t_Kd = "No type";
e_mf_paras = null;
de_mf_paras = null;
Kp_mf_paras = null;
Ki_mf_paras = null;
Kd_mf_paras = null;
Kp = pidInitVal[0];
Ki = pidInitVal[1];
Kd = pidInitVal[2];
A = Kp+Ki+Kd;
B = -2*Kd-Kp;
C = Kd;
}
public float getKp(){
return this.Kp;
}
public float getKi(){
return this.Ki;
}
public float getKd(){
return this.Kd;
}
public float getA(){
return this.A;
}
public float getB(){
return this.B;
}
public float getC(){
return this.C;
}
/**
* 三角隶属函数
* 用于模糊化
* **/
public float trimf(float x, float a, float b, float c){
float u;
if(x>=a && x<=b){
u = (x-a)/(b-a);
}else if(x>b && x<=c){
u = (c-x)/(c-b);
}else{
u = 0.0f;
}
if(Float.isNaN(u)){
u = 0.0f;
}
return u;
}
/**
* 设置模糊规则Matrix
* **/
void setRuleMatrix(int[][] kp_m, int[][] ki_m, int[][] kd_m){
for(int i=0;i= delta_Kp_max){
delta_Kp = delta_Kp_max;
}else if(delta_Kp <= -delta_Kp_max){
delta_Kp = -delta_Kp_max;
}
if(Float.isNaN(delta_Kp)){
delta_Kp = 0;
}
Kp += delta_Kp;
if(Kp < 0){
Kp = 0;
}
// 计算delta_Ki和Ki 解模糊
den = 0; num = 0;
for(int m=0;m<3;m++){
for(int n=0;n<3;n++){
num += u_e[u_e_index[m]] * u_de[u_de_index[n]] * Ki_rule_matrix[u_e_index[m]][u_de_index[n]];
den += u_e[u_e_index[m]] * u_de[u_de_index[n]];
}
}
delta_Ki = num/den;
delta_Ki = Ku_i * delta_Ki; // 为什么计算出来的delta_Kp乘上Ku_p
if(delta_Ki >= delta_Ki_max){
delta_Ki = delta_Ki_max;
}else if(delta_Ki <= -delta_Ki_max){
delta_Ki = -delta_Ki_max;
}
if(Float.isNaN(delta_Ki)){
delta_Ki =0;
}
Ki += delta_Ki;
if(Ki < 0){
Ki = 0;
}
// 计算delta_Kd和Kd 解模糊
den = 0; num = 0;
for(int m=0;m<3;m++){
for(int n=0;n<3;n++){
num += u_e[u_e_index[m]] * u_de[u_de_index[n]] * Kd_rule_matrix[u_e_index[m]][u_de_index[n]];
den += u_e[u_e_index[m]] * u_de[u_de_index[n]];
}
}
delta_Kd = num/den;
delta_Kd = Ku_d * delta_Kd; // 为什么计算出来的delta_Kp乘上Ku_p
if(delta_Kd >= delta_Kd_max){
delta_Kd = delta_Kd_max;
}else if(delta_Kd <= -delta_Kd_max){
delta_Kd = -delta_Kd_max;
}
if(Float.isNaN(delta_Kd)){
delta_Kd = 0;
}
Kd += delta_Kd;
if(Kd < 0){
Kd = 0;
}
/**Ki会不断的累计积分,会变得非常大,这里适当缩小Ki的值**/
if(Ki >1.2){
Ki /= 2;
}
A = Kp + Ki + Kd;
B = -2*Kd - Kp;
C = Kd;
delta_u = A*e +B*e_pre_1 + C*e_pre_2;
delta_u = delta_u / Ke;
// 输出限幅
if(delta_u >= 0.95*target){
delta_u = 0.95f*target;
}else if(delta_u <= -0.95*target){
delta_u = -0.95f*target;
}
e_pre_2 = e_pre_1;
e_pre_1 = e;
return delta_u;
}
}
public class FuzzyPIDMain {
public static final int NB = -3;
public static final int NM = -2;
public static final int NS = -1;
public static final int ZO = 0;
public static final int PS = 1;
public static final int PM = 2;
public static final int PB = 3;
public static void main(String src[]){
float target = 200;
float actual = 0;
float u = 0;
int[][] deltaKpMatrix = {{PB,PB,PM,PM,PS,ZO,ZO},
{PB,PB,PM,PS,PS,ZO,NS},
{PM,PM,PM,PS,ZO,NS,NS},
{PM,PM,PS,ZO,NS,NM,NM},
{PS,PS,ZO,NS,NS,NM,NM},
{PS,ZO,NS,NM,NM,NM,NB},
{ZO,ZO,NM,NM,NM,NB,NB}};
int[][] deltaKiMatrix = {{NB,NB,NM,NM,NS,ZO,ZO},
{NB,NB,NM,NS,NS,ZO,ZO},
{NB,NM,NS,NS,ZO,PS,PS},
{NM,NM,NS,ZO,PS,PM,PM},
{NM,NS,ZO,PS,PS,PM,PB},
{ZO,ZO,PS,PS,PM,PB,PB},
{ZO,ZO,PS,PM,PM,PB,PB}};
int[][] deltaKdMatrix = {{PS,NS,NB,NB,NB,NM,PS},
{PS,NS,NB,NM,NM,NS,ZO},
{ZO,NS,NM,NM,NS,NS,ZO},
{ZO,NS,NS,NS,NS,NS,ZO},
{ZO,ZO,ZO,ZO,ZO,ZO,ZO},
{PB,NS,PS,PS,PS,PS,PB},
{PB,PM,PM,PM,PS,PS,PB}};
float[] e_mf_paras = {-3,-3,-2,-3,-2,-1,-2,-1,0,-1,0,1,0,1,2,1,2,3,2,3,3};
float[] de_mf_paras = {-3,-3,-2,-3,-2,-1,-2,-1,0,-1,0,1,0,1,2,1,2,3,2,3,3};
float[] Kp_mf_paras = {-3,-3,-2,-3,-2,-1,-2,-1,0,-1,0,1,0,1,2,1,2,3,2,3,3};
float[] Ki_mf_paras = {-3,-3,-2,-3,-2,-1,-2,-1,0,-1,0,1,0,1,2,1,2,3,2,3,3};
float[] Kd_mf_paras = {-3,-3,-2,-3,-2,-1,-2,-1,0,-1,0,1,0,1,2,1,2,3,2,3,3};
FuzzyPID fuzzypid = new FuzzyPID(1500f, 650f, 0.3f, 0.9f, 0.6f, 0.01f, 0.04f, 0.01f);
fuzzypid.setMf("trimf",e_mf_paras,"trimf",de_mf_paras,"trimf",Kp_mf_paras,"trimf",Ki_mf_paras,"trimf",Kd_mf_paras);
fuzzypid.setRuleMatrix(deltaKpMatrix,deltaKiMatrix,deltaKdMatrix);
for(int i=0;i<5000;i++){
u = fuzzypid.realize(target, actual);
actual += u;
System.out.println(actual);
// 模拟稳态误差
if(i%1 == 0){
actual -= 5;
}
}
}
}
4 总结
需要注意的是:模糊pid一般需要一个比较接近理想控制效果的pid参数初始值,否者,效果并不理想。