吴恩达Coursera深度学习课程 DeepLearning.ai 编程作业——Convolution model:step by step and application (4.1)

一.Convolutional Neural Networks: Step by Step

Welcome to Course 4’s first assignment! In this assignment, you will implement convolutional (CONV) and pooling (POOL) layers in numpy, including both forward propagation and (optionally) backward propagation.

Notation:

• Superscript $[l]$ denotes an object of the $l^{th}$ layer.

  • Example: $a^{[4]}$ is the $4^{th}$ layer activation. $W^{[5]}$ and $b^{[5]}$ are the $5^{th}$ layer parameters.

• Superscript $(i)$ denotes an object from the $i^{th}$ example.

  • Example: $x^{(i)}$ is the $i^{th}$ training example input.

• Lowerscript $i$ denotes the $i^{th}$ entry of a vector.

  • Example: $a_i^{[l]}$ denotes the $i^{th}$ entry of the activations in layer $l$, assuming this is a fully connected (FC) layer.

• $n_H$, $n_W$ and $n_C$ denote respectively the height, width and number of channels of a given layer. If you want to reference a specific layer $l$, you can also write $n_H^{[l]}$, $n_W^{[l]}$, $n_C^{[l]}$.

• $n_{H_{prev}}$, $n_{W_{prev}}$ and $n_{C_{prev}}$ denote respectively the height, width and number of channels of the previous layer. If referencing a specific layer $l$, this could also be denoted $n_H^{[l-1]}$, $n_W^{[l-1]}$, $n_C^{[l-1]}$.

We assume that you are already familiar with numpy and/or have completed the previous courses of the specialization. Let’s get started!

1 - Packages

Let’s first import all the packages that you will need during this assignment.

• numpy is the fundamental package for scientific computing with Python.
• matplotlib is a library to plot graphs in Python.
• np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work.

import numpy as np
import h5py
import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"]=(5.0,4.0)
plt.rcParams["image.interpolation"]='nearest'
plt.rcParams["image.cmap"]='gray'

np.random.seed(1)

2 - Outline of the Assignment

You will be implementing the building blocks of a convolutional neural network! Each function you will implement will have detailed instructions that will walk you through the steps needed:

• Convolution functions, including:
  • Zero Padding
  • Convolve window
  • Convolution forward
  • Convolution backward (optional)
• Pooling functions, including:
  • Pooling forward
  • Create mask
  • Distribute value
  • Pooling backward (optional)

This notebook will ask you to implement these functions from scratch in numpy. In the next notebook, you will use the TensorFlow equivalents of these functions to build the following model:

Note that for every forward function, there is its corresponding backward equivalent. Hence, at every step of your forward module you will store some parameters in a cache. These parameters are used to compute gradients during backpropagation.

3 - Convolutional Neural Networks

Although programming frameworks make convolutions easy to use, they remain one of the hardest concepts to understand in Deep Learning. A convolution layer transforms an input volume into an output volume of different size, as shown below.

In this part, you will build every step of the convolution layer. You will first implement two helper functions: one for zero padding and the other for computing the convolution function itself.

3.1 - Zero-Padding

Zero-padding adds zeros around the border of an image:

The main benefits of padding are the following:

• It allows you to use a CONV layer without necessarily shrinking the height and width of the volumes. This is important for building deeper networks, since otherwise the height/width would shrink as you go to deeper layers. An important special case is the “same” convolution, in which the height/width is exactly preserved after one layer.

• It helps us keep more of the information at the border of an image. Without padding, very few values at the next layer would be affected by pixels as the edges of an image.

Exercise: Implement the following function, which pads all the images of a batch of examples X with zeros. Use np.pad. Note if you want to pad the array “a” of shape $(5,5,5,5,5)$ with pad = 1 for the 2nd dimension, pad = 3 for the 4th dimension and pad = 0 for the rest, you would do:

a = np.pad(a, ((0,0), (1,1), (0,0), (3,3), (0,0)), 'constant', constant_values = (..,..))
For Example：
>>> a = [1, 2, 3, 4, 5]
>>> np.lib.pad(a, (2,3), 'constant', constant_values=(4, 6))
    array([4, 4, 1, 2, 3, 4, 5, 6, 6, 6])

def zero_pad(X, pad):
    """
    Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image, 
    as illustrated in Figure 1.
    
    Argument:
    X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images,X是一个张量，4维度
    pad -- integer, amount of padding around each image on vertical and horizontal dimensions
    
    Returns:
    X_pad -- padded image of shape (m, n_H + 2*pad, n_W + 2*pad, n_C) #其实就是在n_H 和 n_W这俩个维度填充像素点
    """
    
    ### START CODE HERE ### (≈ 1 line)
    X_pad = np.pad(X,((0,0),(pad,pad),(pad,pad),(0,0)),'constant',constant_values=(0,0))  #置为0
    ### END CODE HERE ###
    
    return X_pad

np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
x_pad = zero_pad(x, 2)
print ("x.shape =", x.shape)
print ("x_pad.shape =", x_pad.shape)
print ("x[1,1] =", x[1,1])
print ("x_pad[1,1] =", x_pad[1,1])

fig, axarr = plt.subplots(1, 2)
axarr[0].set_title('x')
axarr[0].imshow(x[0,:,:,0])
axarr[1].set_title('x_pad')
axarr[1].imshow(x_pad[0,:,:,0])

Expected Output：

('x.shape =', (4, 3, 3, 2))
('x_pad.shape =', (4, 7, 7, 2))
('x[1,1] =', array([[ 0.90085595, -0.68372786],
       [-0.12289023, -0.93576943],
       [-0.26788808,  0.53035547]]))
('x_pad[1,1] =', array([[ 0.,  0.],
       [ 0.,  0.],
       [ 0.,  0.],
       [ 0.,  0.],
       [ 0.,  0.],
       [ 0.,  0.],
       [ 0.,  0.]]))

3.2 - Single step of convolution

In this part, implement a single step of convolution, in which you apply the filter to a single position of the input. This will be used to build a convolutional unit, which:

• Takes an input volume
• Applies a filter at every position of the input
• Outputs another volume (usually of different size)

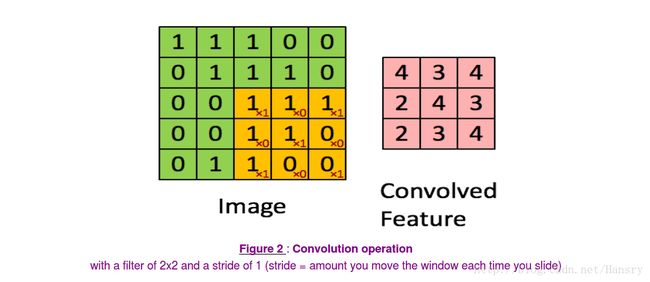
In a computer vision application, each value in the matrix on the left corresponds to a single pixel value, and we convolve a 3x3 filter with the image by multiplying its values element-wise with the original matrix, then summing them up and adding a bias. In this first step of the exercise, you will implement a single step of convolution, corresponding to applying a filter to just one of the positions to get a single real-valued output.

Later in this notebook, you’ll apply this function to multiple positions of the input to implement the full convolutional operation.

Exercise: Implement conv_single_step(). Hint.

def conv_single_step(a_slice_prev, W, b):
    """
    Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation 
    of the previous layer.
    
    Arguments:
    a_slice_prev -- slice of input data of shape (f, f, n_C_prev)
    W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)
    b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)
    
    Returns:
    Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data
    """

    ### START CODE HERE ### (≈ 2 lines of code)
    # Element-wise product between a_slice and W. Do not add the bias yet.
    s = np.multiply(a_slice_prev,W)
    # Sum over all entries of the volume s.
    Z = np.sum(s)
    # Add bias b to Z. Cast b to a float() so that Z results in a scalar value.
    Z = Z+np.float(b)
    ### END CODE HERE ###
    return Z


np.random.seed(1)
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)

Z = conv_single_step(a_slice_prev, W, b)
print("Z =", Z)

Expected output：

('Z =', -6.9990894506802208)

3.3 - Convolutional Neural Networks - Forward pass

In the forward pass, you will take many filters and convolve them on the input. Each ‘convolution’ gives you a 2D matrix output. You will then stack these outputs to get a 3D volume:

Exercise: Implement the function below to convolve the filters W on an input activation A_prev. This function takes as input A_prev, the activations output by the previous layer (for a batch of m inputs), F filters/weights denoted by W, and a bias vector denoted by b, where each filter has its own (single) bias. Finally you also have access to the hyperparameters dictionary which contains the stride and the padding.

Hint:

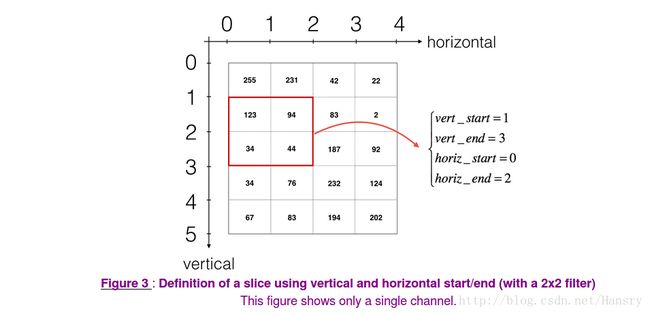
1. To select a 2x2 slice at the upper left corner （左上角）of a matrix “a_prev” (shape (5,5,3)), you would do:

a_slice_prev = a_prev[0:2,0:2,:]

This will be useful when you will define a_slice_prev below, using the start/end indexes you will define.
2. To define a_slice you will need to first define its corners vert_start, vert_end, horiz_start and horiz_end. This figure may be helpful for you to find how each of the corner can be defined using h, w, f and s in the code below.

**Figure 3** : **Definition of a slice using vertical and horizontal start/end (with a 2x2 filter)**
This figure shows only a single channel.

Reminder:
The formulas relating the output shape of the convolution to the input shape is:
$$n_H=\lfloor \frac{n_{H_{prev}}-f+2\times pad}{stride}\rfloor +1$$
$$n_W=\lfloor \frac{n_{W_{prev}}-f+2\times pad}{stride}\rfloor +1$$
$$n_C=\text{number of filters used in the convolution}$$

For this exercise, we won’t worry about vectorization, and will just implement everything with for-loops.

def conv_forward(A_prev, W, b, hparameters):
    """
    Implements the forward propagation for a convolution function
    
    Arguments:
    A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev) #输出
    W -- Weights, numpy array of shape (f, f, n_C_prev, n_C) #滤波器的权重
    b -- Biases, numpy array of shape (1, 1, 1, n_C)  #一个滤波器只需要一个偏置即可
    hparameters -- python dictionary containing "stride" and "pad"
        
    Returns:
    Z -- conv output, numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward() function
    """
    
    ### START CODE HERE ###
    # Retrieve dimensions from A_prev's shape (≈1 line)  
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # Retrieve dimensions from W's shape (≈1 line)
    (f, f, n_C_prev, n_C) = W.shape
    
    # Retrieve information from "hparameters" (≈2 lines)
    stride = hparameters["stride"]
    pad = hparameters["pad"]
    
    # Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines)
    n_H = np.int(math.floor((n_H_prev+2*pad-f)/stride+1))  #函数math.floor 取不大于该数的最大值
    n_W = np.int(math.floor((n_W_prev+2*pad-f)/stride+1))
    
    # Initialize the output volume Z with zeros. (≈1 line)
    Z = np.random.rand(m,n_H,n_W,n_C)
    # Create A_prev_pad by padding A_prev
    A_prev_pad = zero_pad(A_prev,pad)
    
    for i in range(m):                               # loop over the batch of training examples
        a_prev_pad = A_prev_pad[i,:,:,:]                               # Select ith training example's padded activation
        for h in range(n_H):                           # loop over vertical axis of the output volume
            for w in range(n_W):                    # loop over horizontal axis of the output volume
                for c in range(n_C):                # loop over channels (= #filters) of the output volume                    
                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = stride*h
                    vert_end = vert_start+f
                    horiz_start = stride*w
                    horiz_end = horiz_start+f
                    
                   # Use the corners to defie the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line)
                    a_slice_prev = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]
                    # Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line)
                    Z[i, h, w, c] = conv_single_step(a_slice_prev,W[:,:,:,c],b[:,:,:,c])                                 
    ### END CODE HERE ###
    
    # Making sure your output shape is correct
    assert(Z.shape == (m, n_H, n_W, n_C))
    
    # Save information in "cache" for the backprop
    cache = (A_prev, W, b, hparameters)
    
    return Z, cache

np.random.seed(1)
A_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2,
               "stride": 2}

Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
print("Z's mean =", np.mean(Z))
print("Z[3,2,1] =", Z[3,2,1])
print("cache_conv[0][1][2][3] =", cache_conv[0][1][2][3])

Expected output：

("Z's mean =", 0.048995203528855794)
('Z[3,2,1] =', array([-0.61490741, -6.7439236 , -2.55153897,  1.75698377,  3.56208902,
        0.53036437,  5.18531798,  8.75898442]))
('cache_conv[0][1][2][3] =', array([-0.20075807,  0.18656139,  0.41005165]))

Finally, CONV layer should also contain an activation, in which case we would add the following line of code:

# Convolve the window to get back one output neuron
Z[i, h, w, c] = ...
# Apply activation
A[i, h, w, c] = activation(Z[i, h, w, c])

You don’t need to do it here.

4 - Pooling layer

The pooling (POOL) layer reduces the height and width of the input（池化层减小了输入图片的高度和宽度）. It helps reduce computation, as well as helps make feature detectors more invariant to its position in the input. The two types of pooling layers are:

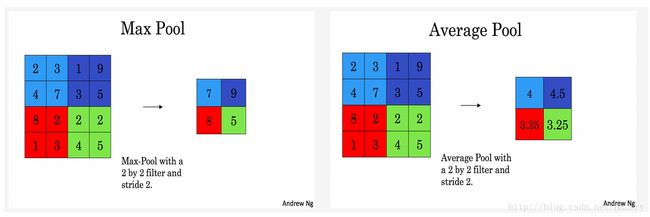
• Max-pooling layer: slides an ($f,f$) window over the input and stores the max value of the window in the output.

• Average-pooling layer: slides an ($f,f$) window over the input and stores the average value of the window in the output.

These pooling layers have no parameters for backpropagation to train. However, they have hyperparameters such as the window size $f$. This specifies the height and width of the fxf window you would compute a max or average over.

4.1 - Forward Pooling

Now, you are going to implement MAX-POOL and AVG-POOL, in the same function.

Exercise: Implement the forward pass of the pooling layer. Follow the hints in the comments below.

Reminder:
As there’s no padding, the formulas binding the output shape of the pooling to the input shape is:
$$n_H=\lfloor \frac{n_{H_{prev}}-f}{stride}\rfloor +1$$
$$n_W=\lfloor \frac{n_{W_{prev}}-f}{stride}\rfloor +1$$
$$n_C=n_{C_{prev}}$$

def pool_forward(A_prev, hparameters, mode = "max"):
    """
    Implements the forward pass of the pooling layer
    
    Arguments:
    A_prev -- Input data, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    hparameters -- python dictionary containing "f" and "stride"
    mode -- the pooling mode you would like to use, defined as a string ("max" or "average")
    
    Returns:
    A -- output of the pool layer, a numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache used in the backward pass of the pooling layer, contains the input and hparameters 
    """
    
    # Retrieve dimensions from the input shape
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # Retrieve hyperparameters from "hparameters"
    f = hparameters["f"]
    stride = hparameters["stride"]
    
    # Define the dimensions of the output
    n_H = int(1 + (n_H_prev - f) / stride)  #池化层是没有padding的，池化层本来作用就是压缩图片
    n_W = int(1 + (n_W_prev - f) / stride)
    n_C = n_C_prev
    
    # Initialize output matrix A
    A = np.zeros((m, n_H, n_W, n_C))              
    
    ### START CODE HERE ###
    for i in range(m):                            # loop over the training examples
        for h in range(n_H):                     # loop on the vertical axis of the output volume
            for w in range(n_W):                 # loop on the horizontal axis of the output volume
                for c in range (n_C):            # loop over the channels of the output volume
                    
                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = stride*h
                    vert_end = vert_start+f
                    horiz_start = stride*w
                    horiz_end = horiz_start+f
                    
                    # Use the corners to define the current slice on the ith training example of A_prev, channel c. (≈1 line)
                    a_prev_slice = A_prev[i,vert_start:vert_end,horiz_start:horiz_end,c]
                    
                    # Compute the pooling operation on the slice. Use an if statment to differentiate the modes. Use np.max/np.mean.
                    if mode == "max":
                        A[i, h, w, c] = np.max(a_prev_slice)   #求最大值
                    elif mode == "average":
                        A[i, h, w, c] = np.average(a_prev_slice) # 求平均值
    
    ### END CODE HERE ###
    
    # Store the input and hparameters in "cache" for pool_backward()
    cache = (A_prev, hparameters)
    
    # Making sure your output shape is correct
    assert(A.shape == (m, n_H, n_W, n_C))
    
    return A, cache

np.random.seed(1)
A_prev = np.random.randn(2, 4, 4, 3)
hparameters = {"stride" : 2, "f": 3}

A, cache = pool_forward(A_prev, hparameters)
print("mode = max")
print("A =", A)
print()
A, cache = pool_forward(A_prev, hparameters, mode = "average")
print("mode = average")
print("A =", A)

Expected output：

mode = max
('A =', array([[[[ 1.74481176,  0.86540763,  1.13376944]]],
       [[[ 1.13162939,  1.51981682,  2.18557541]]]])）
mode = average
('A =', array([[[[ 0.02105773, -0.20328806, -0.40389855]]],
       [[[-0.22154621,  0.51716526,  0.48155844]]]])）

5 - Backpropagation in convolutional neural networks

In modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers don’t need to bother with the details of the backward pass（现代深度学习的框架，只需要实现正向传播功能，因为神经网络的框架会自动接手反向传播的过程，所以深度学习工程师并不需要搞清楚反向传播的过程）. The backward pass for convolutional networks is complicated. If you wish however, you can work through this optional portion of the notebook to get a sense of what backprop in a convolutional network looks like.

When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in convolutional neural networks you can to calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are not trivial and we did not derive them in lecture, but we briefly presented them below.

5.1 - Convolutional layer backward pass

Let’s start by implementing the backward pass for a CONV layer.

5.1.1 - Computing dA:

This is the formula for computing $dA$ with respect to the cost for a certain filter $W_c$ and a given training example:

$$dA+=\sum _{h=0}^{n_H}\sum _{w=0}^{n_W}{W}_c\times d{Z}_{hw}\text{\hspace{1em}(1)}$$

Where $W_c$ is a filter and $d{Z}_{hw}$ is a scalar corresponding to the gradient of the cost with respect to the output of the conv layer Z at the hth row and wth column (corresponding to the dot product taken at the ith stride left and jth stride down). Note that at each time, we multiply the the same filter $W_c$ by a different dZ when updating dA. We do so mainly because when computing the forward propagation, each filter is dotted and summed by a different a_slice. Therefore when computing the backprop for dA, we are just adding the gradients of all the a_slices.

In code, inside the appropriate for-loops, this formula translates into:

da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]

5.1.2 - Computing dW:

This is the formula for computing $d{W}_c$ ($d{W}_c$ is the derivative of one filter) with respect to the loss:

$$d{W}_c+=\sum _{h=0}^{n_H}\sum _{w=0}^{n_W}{a}_{slice}\times d{Z}_{hw}\text{\hspace{1em}(2)}$$

Where $a_{slice}$ corresponds to the slice which was used to generate the acitivation $Z_{ij}$. Hence, this ends up giving us the gradient for $W$ with respect to that slice. Since it is the same $W$, we will just add up all such gradients to get $dW$.

In code, inside the appropriate for-loops, this formula translates into:

dW[:,:,:,c] += a_slice * dZ[i, h, w, c]

5.1.3 - Computing db:

This is the formula for computing $db$ with respect to the cost for a certain filter $W_c$:

$$db=\sum _h\sum _{w}d{Z}_{hw}\text{\hspace{1em}(3)}$$

As you have previously seen in basic neural networks, db is computed by summing $dZ$. In this case, you are just summing over all the gradients of the conv output (Z) with respect to the cost.

In code, inside the appropriate for-loops, this formula translates into:

db[:,:,:,c] += dZ[i, h, w, c]

Exercise: Implement the conv_backward function below. You should sum over all the training examples, filters, heights, and widths. You should then compute the derivatives using formulas 1, 2 and 3 above.

def conv_backward(dZ, cache):
    """
    Implement the backward propagation for a convolution function
    
    Arguments:
    dZ -- gradient of the cost with respect to the output of the conv layer (Z), numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward(), output of conv_forward()
    
    Returns:
    dA_prev -- gradient of the cost with respect to the input of the conv layer (A_prev),
               numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    dW -- gradient of the cost with respect to the weights of the conv layer (W)
          numpy array of shape (f, f, n_C_prev, n_C)
    db -- gradient of the cost with respect to the biases of the conv layer (b)
          numpy array of shape (1, 1, 1, n_C)
    """
    
    ### START CODE HERE ###
    # Retrieve information from "cache"
    (A_prev, W, b, hparameters) = cache    
    # Retrieve dimensions from A_prev's shape
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape   
    # Retrieve dimensions from W's shape
    (f, f, n_C_prev, n_C) = W.shape    
    # Retrieve information from "hparameters"
    stride = hparameters["stride"]
    pad = hparameters["pad"]    
    # Retrieve dimensions from dZ's shape
    (m, n_H, n_W, n_C) = dZ.shape    
    # Initialize dA_prev, dW, db with the correct shapes
    dA_prev = np.zeros((m,n_H_prev,n_W_prev,n_C_prev))                           
    dW = np.zeros((f,f,n_C_prev,n_C))
    db = np.zeros((1,1,1,n_C))
    # Pad A_prev and dA_prev
    A_prev_pad = zero_pad(A_prev, pad)
    dA_prev_pad = np.zeros(A_prev_pad.shape)
    for i in range(m):                       # loop over the training examples        
        # select ith training example from A_prev_pad and dA_prev_pad
        a_prev_pad = A_prev_pad[i,:,:,:]
        da_prev_pad = dA_prev_pad[i,:,:,:]        
        for h in range(n_H):                   # loop over vertical axis of the output volume
            for w in range(n_W):               # loop over horizontal axis of the output volume
                for c in range(n_C):           # loop over the channels of the output volume                    
                    # Find the corners of the current "slice"
                    vert_start = stride*h
                    vert_end = vert_start+f
                    horiz_start = stride*w
                    horiz_end = horiz_start+f
                    # Use the corners to define the slice from a_prev_pad
                    a_slice = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]
                    # Update gradients for the window and the filter's parameters using the code formulas given above
                    da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] +=  W[:,:,:,c] * dZ[i,h,w,c]
                    dW[:,:,:,c] += a_slice * dZ[i,h,w,c]
                    db[:,:,:,c] += dZ[i,h,w,c]                   
        # Set the ith training example's dA_prev to the unpaded da_prev_pad (Hint: use X[pad:-pad, pad:-pad, :])
        dA_prev[i, :, :, :] = da_prev_pad[pad:-pad,pad:-pad,:]
    ### END CODE HERE ###
    
    # Making sure your output shape is correct
    assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
    
    return dA_prev, dW, db

np.random.seed(1)
dA, dW, db = conv_backward(Z, cache_conv)
print("dA_mean =", np.mean(dA))
print("dW_mean =", np.mean(dW))
print("db_mean =", np.mean(db))

Expected output：

('dA_mean =', 1.4524377775388075)
('dW_mean =', 1.7269914583139097)
('db_mean =', 7.8392325646168377)

5.2 Pooling layer - backward pass

Next, let’s implement the backward pass for the pooling layer, starting with the MAX-POOL layer. Even though a pooling layer has no parameters for backprop to update, you still need to backpropagation the gradient through the pooling layer in order to compute gradients for layers that came before the pooling layer.

5.2.1 Max pooling - backward pass

Before jumping into the backpropagation of the pooling layer, you are going to build a helper function called create_mask_from_window() which does the following:

$$X=\left[\begin{array}{ccc}1& & 3\\ 4& & 2\end{array}\right]\to M=\left[\begin{array}{ccc}0& & 0\\ 1& & 0\end{array}\right]\text{\hspace{1em}(4)}$$

As you can see, this function creates a “mask” matrix which keeps track of where the maximum of the matrix is. True (1) indicates the position of the maximum in X, the other entries are False (0). You’ll see later that the backward pass for average pooling will be similar to this but using a different mask. （构造一个函数，检测矩阵中最大的元素，最大的置1，其他置0）

Exercise: Implement create_mask_from_window(). This function will be helpful for pooling backward.
Hints:

• np.max() may be helpful. It computes the maximum of an array.
• If you have a matrix X and a scalar x: A = (X == x) will return a matrix A of the same size as X such that:

A[i,j] = True if X[i,j] = x
A[i,j] = False if X[i,j] != x

• Here, you don’t need to consider cases where there are several maxima in a matrix.

def create_mask_from_window(x):
    """
    Creates a mask from an input matrix x, to identify the max entry of x.
    
    Arguments:
    x -- Array of shape (f, f)
    
    Returns:
    mask -- Array of the same shape as window, contains a True at the position corresponding to the max entry of x.
    """   
    ### START CODE HERE ### (≈1 line)
    mask = (x==np.max(x))
    ### END CODE HERE ###    
    return mask

np.random.seed(1)
x = np.random.randn(2,3)
mask = create_mask_from_window(x)
print('x = ', x)
print("mask = ", mask)

Expected output：

('x = ', array([[ 1.62434536, -0.61175641, -0.52817175],
       [-1.07296862,  0.86540763, -2.3015387 ]]))
('mask = ', array([[ True, False, False],
       [False, False, False]], dtype=bool))

Why do we keep track of the position of the max? It’s because this is the input value that ultimately influenced the output, and therefore the cost. Backprop is computing gradients with respect to the cost, so anything that influences the ultimate cost should have a non-zero gradient. So, backprop will “propagate” the gradient back to this particular input value that had influenced the cost（由于最大池化层将卷积核扫过的最大的值赋值给了该层输出，影响了最后的输出，即将图片的高和宽压缩了，所以在反向传播的过程中，所有影响最终cost输出的都不能为了，所以要跟踪其最大值的位置，保证其在不能为0）.

5.2.2 - Average pooling - backward pass

In max pooling, for each input window, all the “influence” on the output came from a single input value–the max. In average pooling, every element of the input window has equal influence on the output. So to implement backprop, you will now implement a helper function that reflects this.

For example if we did average pooling in the forward pass using a 2x2 filter, then the mask you’ll use for the backward pass will look like:
$$dZ=1\to dZ=\left[\begin{array}{ccc}1/4& & 1/4\\ 1/4& & 1/4\end{array}\right]\text{\hspace{1em}(5)}$$

This implies that each position in the $dZ$ matrix contributes equally to output because in the forward pass, we took an average.

Exercise: Implement the function below to equally distribute a value dz through a matrix of dimension shape. Hint

def distribute_value(dz, shape):
    """
    Distributes the input value in the matrix of dimension shape
    
    Arguments:
    dz -- input scalar
    shape -- the shape (n_H, n_W) of the output matrix for which we want to distribute the value of dz
    
    Returns:
    a -- Array of size (n_H, n_W) for which we distributed the value of dz
    """
    
    ### START CODE HERE ###
    # Retrieve dimensions from shape (≈1 line)
    (n_H, n_W) = shape
    # Compute the value to distribute on the matrix (≈1 line)
    average = np.float(dz)/np.float(n_H*n_W)
    # Create a matrix where every entry is the "average" value (≈1 line)
    a = np.ones((n_H,n_W))*average
    ### END CODE HERE ###
    return a

a = distribute_value(2, (2,2))
print('distributed value =', a)

Expected output：

('distributed value =', array([[ 0.5,  0.5],
       [ 0.5,  0.5]]))

5.2.3 Putting it together: Pooling backward

You now have everything you need to compute backward propagation on a pooling layer.

Exercise: Implement the pool_backward function in both modes ("max" and "average"). You will once again use 4 for-loops (iterating over training examples, height, width, and channels). You should use an if/elif statement to see if the mode is equal to 'max' or 'average'. If it is equal to ‘average’ you should use the distribute_value() function you implemented above to create a matrix of the same shape as a_slice. Otherwise, the mode is equal to ‘max’, and you will create a mask with create_mask_from_window() and multiply it by the corresponding value of dZ.

def pool_backward(dA, cache, mode = "max"):
    """
    Implements the backward pass of the pooling layer
    
    Arguments:
    dA -- gradient of cost with respect to the output of the pooling layer, same shape as A
    cache -- cache output from the forward pass of the pooling layer, contains the layer's input and hparameters 
    mode -- the pooling mode you would like to use, defined as a string ("max" or "average")
    
    Returns:
    dA_prev -- gradient of cost with respect to the input of the pooling layer, same shape as A_prev
    """
    
    ### START CODE HERE ###
    
    # Retrieve information from cache (≈1 line)
    (A_prev, hparameters) = cache
    # Retrieve hyperparameters from "hparameters" (≈2 lines)
    stride = hparameters["stride"]
    f = hparameters["f"]
    # Retrieve dimensions from A_prev's shape and dA's shape (≈2 lines)
    m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape
    m, n_H, n_W, n_C = dA.shape
    # Initialize dA_prev with zeros (≈1 line)
    dA_prev = np.zeros((m,n_H_prev,n_W_prev,n_C_prev))
    for i in range(m):                       # loop over the training examples
        # select training example from A_prev (≈1 line)
        a_prev = A_prev[i,:,:,:]
        for h in range(n_H):                   # loop on the vertical axis
            for w in range(n_W):               # loop on the horizontal axis
                for c in range(n_C):           # loop over the channels (depth)      
                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = stride*h
                    vert_end = vert_start+f
                    horiz_start = stride*w
                    horiz_end = horiz_start+f
                    
                    # Compute the backward propagation in both modes.
                    if mode == "max":
                        # Use the corners and "c" to define the current slice from a_prev (≈1 line)
                        a_prev_slice = a_prev[vert_start:vert_end,horiz_start:horiz_end,c]
                        # Create the mask from a_prev_slice (≈1 line)
                        mask = create_mask_from_window(a_prev_slice)
                        # Set dA_prev to be dA_prev + (the mask multiplied by the correct entry of dA) (≈1 line)
                        dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += np.multiply(mask,dA[i,h,w,c])
                        
                    elif mode == "average":
                        
                        # Get the value a from dA (≈1 line)
                        da = dA[i,h,w,c]
                        # Define the shape of the filter as fxf (≈1 line)
                        shape = (f,f)
                        # Distribute it to get the correct slice of dA_prev. i.e. Add the distributed value of da. (≈1 line)
                        dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += distribute_value(da, shape)
                        
    # Making sure your output shape is correct
    assert(dA_prev.shape == A_prev.shape)
    return dA_prev

np.random.seed(1)
A_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride" : 1, "f": 2}
A, cache = pool_forward(A_prev, hparameters)
dA = np.random.randn(5, 4, 2, 2)

dA_prev = pool_backward(dA, cache, mode = "max")
print("mode = max")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1])  
print()
dA_prev = pool_backward(dA, cache, mode = "average")
print("mode = average")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1]) 

Expected output：

mode = max
('mean of dA = ', 0.14571390272918056)
('dA_prev[1,1] = ', array([[ 0.        ,  0.        ],
       [ 5.05844394, -1.68282702],
       [ 0.        ,  0.        ]]))
()
mode = average
('mean of dA = ', 0.14571390272918056)
('dA_prev[1,1] = ', array([[ 0.08485462,  0.2787552 ],
       [ 1.26461098, -0.25749373],
       [ 1.17975636, -0.53624893]]))

Congratulations !

Congratulation on completing this assignment. You now understand how convolutional neural networks work. You have implemented all the building blocks of a neural network. In the next assignment you will implement a ConvNet using TensorFlow.

二.Convolutional Neural Networks: Application

Welcome to Course 4’s second assignment! In this notebook, you will:

• Implement helper functions that you will use when implementing a TensorFlow model
• Implement a fully functioning ConvNet using TensorFlow

After this assignment you will be able to:

• Build and train a ConvNet in TensorFlow for a classification problem

We assume here that you are already familiar with TensorFlow. If you are not, please refer the TensorFlow Tutorial of the third week of Course 2 (“Improving deep neural networks”).

1.0 - TensorFlow model

In the previous assignment, you built helper functions using numpy to understand the mechanics behind convolutional neural networks. Most practical applications of deep learning today are built using programming frameworks, which have many built-in functions you can simply call.

As usual, we will start by loading in the packages.

`import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
import tensorflow as tf
from tensorflow.python.framework import ops
from cnn_utils import *

%matplotlib inline
np.random.seed(1)`

Run the next cell to load the “SIGNS” dataset you are going to use.

X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

As a reminder, the SIGNS dataset is a collection of 6 signs representing numbers from 0 to 5.

The next cell will show you an example of a labelled image in the dataset. Feel free to change the value of index below and re-run to see different examples.

In Course 2, you had built a fully-connected network for this dataset. But since this is an image dataset, it is more natural to apply a ConvNet to it.

To get started, let’s examine the shapes of your data.

X_train = X_train_orig/255.
X_test = X_test_orig/255.    #归一化
Y_train = convert_to_one_hot(Y_train_orig, 6).T  #转化为6个分类
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}

Exptected output:

number of training examples = 1080
number of test examples = 120
X_train shape: (1080, 64, 64, 3)
Y_train shape: (1080, 6)
X_test shape: (120, 64, 64, 3)
Y_test shape: (120, 6)

1.1 - Create placeholders

TensorFlow requires that you create placeholders for the input data that will be fed into the model when running the session.

Exercise: Implement the function below to create placeholders for the input image X and the output Y. You should not define the number of training examples for the moment. To do so, you could use “None” as the batch size, it will give you the flexibility to choose it later. Hence X should be of dimension [None, n_H0, n_W0, n_C0] and Y should be of dimension [None, n_y]. Hint.

# GRADED FUNCTION: create_placeholders

def create_placeholders(n_H0, n_W0, n_C0, n_y):
    """
    Creates the placeholders for the tensorflow session.
    
    Arguments:
    n_H0 -- scalar, height of an input image
    n_W0 -- scalar, width of an input image
    n_C0 -- scalar, number of channels of the input
    n_y -- scalar, number of classes
        
    Returns:
    X -- placeholder for the data input, of shape [None, n_H0, n_W0, n_C0] and dtype "float"
    Y -- placeholder for the input labels, of shape [None, n_y] and dtype "float"
    """

    ### START CODE HERE ### (≈2 lines)
    X = tf.placeholder(tf.float32,shape=[None,n_H0,n_W0,n_C0])  #None代表的是样本  
    Y = tf.placeholder(tf.float32,shape=[None,n_y])
    ### END CODE HERE ###
    
    return X, Y

X, Y = create_placeholders(64, 64, 3, 6)
print ("X = " + str(X))
print ("Y = " + str(Y))

Expected output:

X = Tensor("Placeholder:0", shape=(?, 64, 64, 3), dtype=float32)
Y = Tensor("Placeholder_1:0", shape=(?, 6), dtype=float32)

1.2 - Initialize parameters

You will initialize weights/filters $W1$ and $W2$ using tf.contrib.layers.xavier_initializer(seed = 0). You don’t need to worry about bias variables as you will soon see that TensorFlow functions take care of the bias. Note also that you will only initialize the weights/filters for the conv2d functions. TensorFlow initializes the layers for the fully connected part automatically. We will talk more about that later in this assignment.

Exercise: Implement initialize_parameters(). The dimensions for each group of filters are provided below. Reminder - to initialize a parameter $W$ of shape [1,2,3,4] in Tensorflow, use:

W = tf.get_variable("W", [1,2,3,4], initializer = ...)

def initialize_parameters():
    """
    Initializes weight parameters to build a neural network with tensorflow. The shapes are:
                        W1 : [4, 4, 3, 8]
                        W2 : [2, 2, 8, 16]
    Returns:
    parameters -- a dictionary of tensors containing W1, W2
    """
    
    tf.set_random_seed(1)                              # so that your "random" numbers match ours
        
    ### START CODE HERE ### (approx. 2 lines of code)
    W1 = tf.get_variable("W1",[4,4,3,8],initializer=tf.contrib.layers.xavier_initializer(seed=0))
    W2 = tf.get_variable("W2",[2,2,8,16],initializer=tf.contrib.layers.xavier_initializer(seed=0))
    ### END CODE HERE ###

    parameters = {"W1": W1,
                  "W2": W2}
    
    return parameters

1.2 - Forward propagation

In TensorFlow, there are built-in functions that carry out the convolution steps for you.

• tf.nn.conv2d(X,W1, strides = [1,s,s,1], padding = ‘SAME’): given an input $X$ and a group of filters $W1$, this function convolves $W1$'s filters on X. The third input ([1,f,f,1]) represents the strides for each dimension of the input (m, n_H_prev, n_W_prev, n_C_prev). You can read the full documentation here

• tf.nn.max_pool(A, ksize = [1,f,f,1], strides = [1,s,s,1], padding = ‘SAME’): given an input A, this function uses a window of size (f, f) and strides of size (s, s) to carry out max pooling over each window. You can read the full documentation here

• tf.nn.relu(Z1): computes the elementwise ReLU of Z1 (which can be any shape). You can read the full documentation here.

• tf.contrib.layers.flatten§: given an input P, this function flattens each example into a 1D vector it while maintaining the batch-size. It returns a flattened tensor with shape [batch_size, k]. You can read the full documentation here.

• tf.contrib.layers.fully_connected(F, num_outputs): given a the flattened input F, it returns the output computed using a fully connected layer. You can read the full documentation here.

In the last function above (tf.contrib.layers.fully_connected), the fully connected layer automatically initializes weights in the graph and keeps on training them as you train the model. Hence, you did not need to initialize those weights when initializing the parameters.

Exercise:

Implement the forward_propagation function below to build the following model: CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED. You should use the functions above.

In detail, we will use the following parameters for all the steps:
- Conv2D: stride 1, padding is “SAME”
- ReLU
- Max pool: Use an 8 by 8 filter size and an 8 by 8 stride, padding is “SAME”
- Conv2D: stride 1, padding is “SAME”
- ReLU
- Max pool: Use a 4 by 4 filter size and a 4 by 4 stride, padding is “SAME”
- Flatten the previous output.
- FULLYCONNECTED (FC) layer: Apply a fully connected layer without an non-linear activation function. Do not call the softmax here. This will result in 6 neurons in the output layer, which then get passed later to a softmax. In TensorFlow, the softmax and cost function are lumped together into a single function, which you’ll call in a different function when computing the cost.

def forward_propagation(X, parameters):
    """
    Implements the forward propagation for the model:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
    
    Arguments:
    X -- input dataset placeholder, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "W2"
                  the shapes are given in initialize_parameters

    Returns:
    Z3 -- the output of the last LINEAR unit
    """
    
    # Retrieve the parameters from the dictionary "parameters" 
    W1 = parameters['W1']
    W2 = parameters['W2']
    
    ### START CODE HERE ###
    # CONV2D: stride of 1, padding 'SAME'
    Z1 = tf.nn.conv2d(X,W1,strides=[1,1,1,1],padding='SAME')
    # RELU
    A1 = tf.nn.relu(Z1)
    # MAXPOOL: window 8x8, sride 8, padding 'SAME'
    P1 = tf.nn.max_pool(A1,ksize=[1,8,8,1],strides=[1,8,8,1],padding='SAME')
    # CONV2D: filters W2, stride 1, padding 'SAME'
    Z2 = tf.nn.conv2d(P1,W2,strides=[1,1,1,1],padding='SAME')
    # RELU
    A2 = tf.nn.relu(Z2)
    # MAXPOOL: window 4x4, stride 4, padding 'SAME'
    P2 = tf.nn.max_pool(A2,ksize=[1,4,4,1],strides=[1,4,4,1],padding='SAME')
    # FLATTEN
    P2 = tf.contrib.layers.flatten(P2)
    # FULLY-CONNECTED without non-linear activation function (not not call softmax).
    # 6 neurons in output layer. Hint: one of the arguments should be "activation_fn=None" 
    Z3 = tf.contrib.layers.fully_connected(P2,6,activation_fn=None)
    ### END CODE HERE ###

    return Z3

1.3 - Compute cost

Implement the compute cost function below. You might find these two functions helpful:

• tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y): computes the softmax entropy loss. This function both computes the softmax activation function as well as the resulting loss. You can check the full documentation here.
• tf.reduce_mean: computes the mean of elements across dimensions of a tensor. Use this to sum the losses over all the examples to get the overall cost. You can check the full documentation here.

** Exercise**: Compute the cost below using the function above.

def compute_cost(Z3, Y):
    """
    Computes the cost
    
    Arguments:
    Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
    Y -- "true" labels vector placeholder, same shape as Z3
    
    Returns:
    cost - Tensor of the cost function
    """
    
    ### START CODE HERE ### (1 line of code)
    cost = tf.nn.softmax_cross_entropy_with_logits(logits=Z3,labels=Y)
    cost=tf.reduce_mean(cost)
    ### END CODE HERE ###
    
    return cost

1.4 Model

Finally you will merge the helper functions you implemented above to build a model. You will train it on the SIGNS dataset.

You have implemented random_mini_batches() in the Optimization programming assignment of course 2. Remember that this function returns a list of mini-batches.

Exercise: Complete the function below.

The model below should:

• create placeholders
• initialize parameters
• forward propagate
• compute the cost
• create an optimizer

Finally you will create a session and run a for loop for num_epochs, get the mini-batches, and then for each mini-batch you will optimize the function. Hint for initializing the variables
def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.009,
num_epochs = 100, minibatch_size = 64, print_cost = True):
“”"
Implements a three-layer ConvNet in Tensorflow:
CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

Arguments:
X_train -- training set, of shape (None, 64, 64, 3)
Y_train -- test set, of shape (None, n_y = 6)
X_test -- training set, of shape (None, 64, 64, 3)
Y_test -- test set, of shape (None, n_y = 6)
learning_rate -- learning rate of the optimization
num_epochs -- number of epochs of the optimization loop
minibatch_size -- size of a minibatch
print_cost -- True to print the cost every 100 epochs

Returns:
train_accuracy -- real number, accuracy on the train set (X_train)
test_accuracy -- real number, testing accuracy on the test set (X_test)
parameters -- parameters learnt by the model. They can then be used to predict.
"""

ops.reset_default_graph()                         # to be able to rerun the model without overwriting tf variables
tf.set_random_seed(1)                             # to keep results consistent (tensorflow seed)
seed = 3                                          # to keep results consistent (numpy seed)
(m, n_H0, n_W0, n_C0) = X_train.shape             
n_y = Y_train.shape[1]                            
costs = []                                        # To keep track of the cost

# Create Placeholders of the correct shape
### START CODE HERE ### (1 line)
X, Y = create_placeholders(n_H0,n_W0,n_C0,n_y)
### END CODE HERE ###

# Initialize parameters
### START CODE HERE ### (1 line)
parameters = initialize_parameters()
### END CODE HERE ###

# Forward propagation: Build the forward propagation in the tensorflow graph
### START CODE HERE ### (1 line)
Z3 = forward_propagation(X, parameters)
### END CODE HERE ###

# Cost function: Add cost function to tensorflow graph
### START CODE HERE ### (1 line)
cost = compute_cost(Z3, Y)
### END CODE HERE ###

# Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.
### START CODE HERE ### (1 line)
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
### END CODE HERE ###

# Initialize all the variables globally
init = tf.global_variables_initializer()
 
# Start the session to compute the tensorflow graph
with tf.Session() as sess:
    
    # Run the initialization
    sess.run(init)
    
    # Do the training loop
    for epoch in range(num_epochs):

        minibatch_cost = 0.
        num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
        seed = seed + 1
        minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)

        for minibatch in minibatches:

            # Select a minibatch
            (minibatch_X, minibatch_Y) = minibatch
            # IMPORTANT: The line that runs the graph on a minibatch.
            # Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).
            ### START CODE HERE ### (1 line)
            _ , temp_cost = sess.run([optimizer,cost],feed_dict={X:minibatch_X,Y:minibatch_Y})
            ### END CODE HERE ##                ### END CODE HERE ####
            
            minibatch_cost += temp_cost / num_minibatches
            

        # Print the cost every epoch
        if print_cost == True and epoch % 5 == 0:
            print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
        if print_cost == True and epoch % 1 == 0:
            costs.append(minibatch_cost)
    
    
    # plot the cost
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per tens)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()

    # Calculate the correct predictions
    predict_op = tf.argmax(Z3, 1)
    correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))
    
    # Calculate accuracy on the test set
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
    print(accuracy)
    train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
    test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
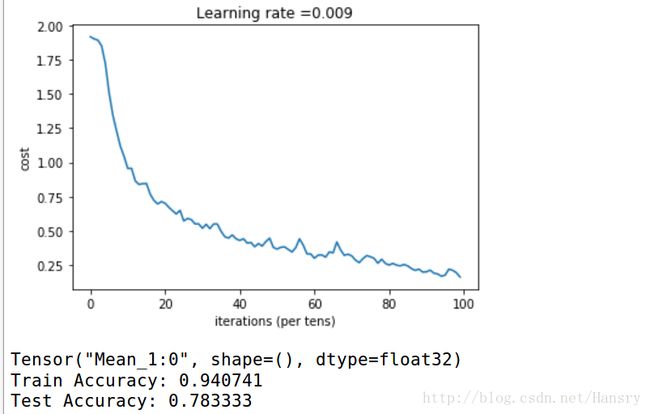
    print("Train Accuracy:", train_accuracy)
    print("Test Accuracy:", test_accuracy)
            
    return train_accuracy, test_accuracy, parameters

_, _, parameters = model(X_train, Y_train, X_test, Y_test)

Cost after epoch 0: 1.917929
Cost after epoch 5: 1.506757
Cost after epoch 10: 0.955359
Cost after epoch 15: 0.845802
Cost after epoch 20: 0.701174
Cost after epoch 25: 0.571977
Cost after epoch 30: 0.518435
Cost after epoch 35: 0.495806
Cost after epoch 40: 0.429827
Cost after epoch 45: 0.407291
Cost after epoch 50: 0.366394
Cost after epoch 55: 0.376922
Cost after epoch 60: 0.299491
Cost after epoch 65: 0.338870
Cost after epoch 70: 0.316400
Cost after epoch 75: 0.310413
Cost after epoch 80: 0.249549
Cost after epoch 85: 0.243457
Cost after epoch 90: 0.200031
Cost after epoch 95: 0.175452