神经网络(Neural Network)

动机(Motivation)

对于非线性分类问题，如果用多元线性回归进行分类，需要构造许多高次项，导致特征特多学习参数过多，从而复杂度太高。

神经网络(Neural Network)

一个简单的神经网络如下图所示，每一个圆圈表示一个神经元，每个神经元接收上一层神经元的输出作为其输入，同时其输出信号到下一层，其中每一层的第一个神经元称为bias unit，它是额外加入的其值为1，通常用+1表示,下图用虚线画出。

 

符号说明：

• a(j)i 表示第j层网络的第i个神经元，例如下图 a(2)1 就表示第二层的第一个神经元
• θ(j) 表示从第 j 层到第 j+1 层的权重矩阵，例如下图所有的 θ(1) 表示从第一层到第二层的权重矩阵
• θ(j)uv 表示从第j层的第v个神经元到第j+1层的第u个神经的权重，例如下图中 θ(1)23 表示从第一层的第3个神经元到第二层的第2个神经元的权重，需要注意到的是下标uv是指v->u的权重而不是u->v，下图也给出了第一层到第二层的所有权重标注
• 一般地，如果第j层有 sj 个神经元（不包括bias神经元），第j+1层有 sj+1 个神经元（也不包括bias神经元），那么权重矩阵 θj 的维度是 (sj+1×sj+1)

前向传播(Forward Propagration, FP)

后一层的神经元的值根据前一层神经元的值的改变而改变，以上图为例，第二层的神经元的更新方式为

a(2)1=g(θ(1)10x0+θ(1)11x1+θ(1)12x2+θ(1)13x3)

a(2)2=g(θ(1)20x0+θ(1)21x1+θ(1)22x2+θ(1)23x3)

a(2)3=g(θ(1)30x0+θ(1)31x1+θ(1)32x2+θ(1)33x3)

a(2)4=g(θ(1)40x0+θ(1)41x1+θ(1)42x2+θ(1)43x3)

其中g(z)为sigmoid函数，即 g(z)=11+e−z

1. 向量化实现(Vectorized Implementation)

如果我们以向量角度来看待上述的更新公式，定义

a(1)=x=⎡⎣⎢⎢⎢x0x1x2x3⎤⎦⎥⎥⎥     z(2)=⎡⎣⎢⎢⎢z(2)1z(2)1z(2)1⎤⎦⎥⎥⎥     θ(1)=⎡⎣⎢⎢⎢θ(1)10θ(1)20θ(1)30θ(1)11θ(1)21θ(1)31θ(1)12θ(1)22θ(1)32θ(1)13θ(1)23θ(1)33⎤⎦⎥⎥⎥

则更新公式可以简化为

z(2)=θ(1)a(1)

a(2)=g(z(2))

z(3)=θ(2)a(2)

a(3)=g(z(3))=hθ(x)

可以看到，我们由第一层的值，计算第二层的值；由第二层的值，计算第三层的值，得到预测的输出，计算的方式一层一层往前走的，这也是前向传播的名称由来。

2. 与Logistic回归的联系

考虑上图没有隐藏层的神经网络，其中 x=⎡⎣⎢⎢⎢x0x1x2x3⎤⎦⎥⎥⎥ ， θ=[θ0θ1θ2θ3] ，则我们有 hθ(x)=a(2)1=g(z(1))=g(θx)=g(x0θ0+x1θ1+x2θ2+x3θ3) ，可以看到这正是Logistic回归的假设函数！！！这种关系表明Logistic是回归是不含隐藏层的特殊神经网络，神经网络从某种程度上来说是对logistic回归的推广。

神经网络示例

对于如下图所示的线性不可分的分类问题，(0,0)(1,1)为一类(0,1)(1,0)为另一类，神经网络可以解决（见5）。首先需要一些简单的神经网络(1-4)，其中图和真值表结合可以清楚的看出其功能，不再赘述。

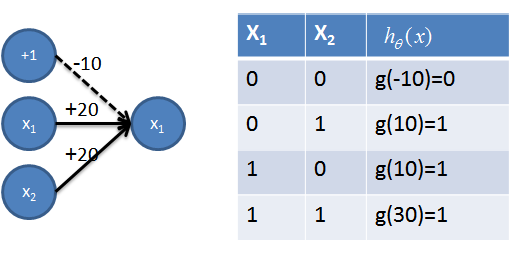
1. 实现AND操作

2. 实现OR操作

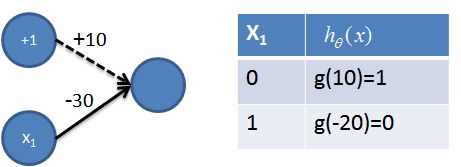
3. 实现非操作

4. 实现NAND=((not x1) and (not x2))操作

5. 组合实现NXOR=NOT(x1 XOR x2) 操作 

该神经网络用到了之前的AND操作（用红色表示）、NAND操作（用青色表示）和OR操作（用橙色表示），从真值表可以看出，该神经网络成功地将(0, 0)(1,1)分为一类，(1,0)(0,1)分为一类，很好解决了线性不可分的问题。

神经网络的代价函数(含正则项)

J(Θ)=−1m[∑i=1m∑k=1Ky(i)klog(hθ(x(i)))k+(1−y(i)k)log(1−(hθ(x(i)))k)]+λ2m∑l=1L−1∑i=1sl∑j=1sl+1(Θ(l)ji)2

符号说明：

• m — 训练example的数量
• K  — 最后一层（输出层）的神经元的个数，也等于分类数（分 K 类， K≥3 ）
• y(i)k — 第 i 个训练exmaple的输出(长度为 K 个向量)的第 k 个分量值
• (hθ(x(i)))k — 对第 i 个example用神经网络预测的输出(长度为 K 的向量)的第 k 个分量值
• L  — 神经网络总共的层数（包括输入层和输出层）
• Θ(l)  — 第 l 层到第 l+1 层的权重矩阵
• sl  — 第 l 层神经元的个数, 注意 i 从1开始计数，bias神经元的权重不算在正则项内
• sl+1  — 第 l+1 层神经元的个数

参考文献

 [1] Andrew Ng Coursera 公开课第四周

 [2] Neural Networks. https://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol4/cs11/report.html

 [3] The nature of code. http://natureofcode.com/book/chapter-10-neural-networks/

 [4] A Basic Introduction To Neural Networks. http://pages.cs.wisc.edu/~bolo/shipyard/neural/local.html