用图网络做知识图谱实体对齐

本文是对Cross-lingual Knowledge Graph Alignment via Graph Convolutional Networks的深度解读。

使用GNN做实体对齐的先锋

多语言知识图谱（KG）包含多种语言的结构化知识，是跨语言NLP应用的有用资源，跨语言KG的实体对齐是将实体与它在其他语言的对应实体进行匹配的过程，在多语言知识图谱中丰富跨语言链接的一个重要途径。本文提出一个新的利用GCN进行跨语言实体对齐的方法。在给定种子实体对的前提下，训练一个GCN，将每种语言的实体和关系嵌入到一个统一的空间中，，然后基于实体向量的相似度寻找对齐的实体。属性和结构都学习一个表示，最后基于这两种表示进行实体对齐。

0前言

知识图谱以机器可读的形式表示人类知识，已经成为多个AI和NLP任务的重要基础。跨语言实体对齐多语言知识图谱连接多余语言的鸿沟中起重要作用，但是在很多KG中，已经对齐的实体只占一小部分。所以要通过实体对齐对齐更多的实体。

现有的基于嵌入的实体对齐方法都是在一个优化问题中联合地建模跨语言知识和单语言知识，这两种知识的损失必须互相调整。还有一点，现有的方法虽然使用了属性，但都未使用属性值。

基于以上的考虑，本文提出一个新的基于嵌入的KG对齐方法，它使用GCN直接建模实体间的等价关系。GCN是能直接在图上操作的卷积网络，它通过编码节点的邻居信息生成节点的嵌入。在KG中，两个等价实体的邻接实体中往往包含其他等价的实体，本文利用GCN生成邻居自适应的实体嵌入，基于此来发现对齐的实体。本文的方法还同时考虑了实体的属性值。

1问题描述

KG用三元组表示现实世界的知识，这里考虑两类知识：关系三元组和属性三元组，关系三元组表示实体间的关系，属性三元组描述实体的属性。将一个KG表示为,其中分别是实体、关系、属性的集合。是关系三元组的集合，是属性三元组的集合。令和是两个知识图谱，且种子实体的集合。我们将跨语言实体对齐任务定义为基于现有的对齐数据寻找新的对齐数据的任务。在很多多语言KG中，不同语言实体间的连接可以看做种子，基于这些种子可找到更多的对齐。

3主要方法

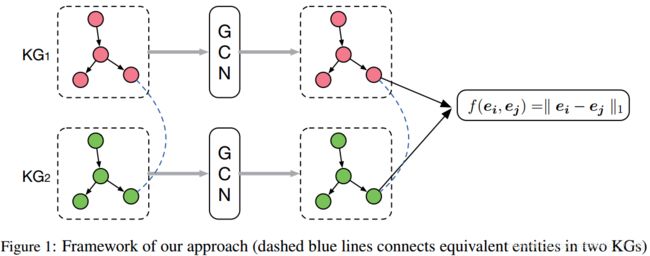
方法的框架如图1所示

给定两个知识图谱和，和一组预先对齐的实体,本文的方法基于GCN的实体嵌入找到新的对齐。方法的基本思想是利用GCN将来自于不同语言的实体嵌入到一个统一的向量空间中，同时希望对齐的实体间距离更近。

GCN是一类直接在图上进行操作的神经网络。它的输入是节点的特征向量和图的结构，目的是输出节点级的实体嵌入。GCN将节点的邻居信息编码为实值向量。在实体对齐问题上，假设：1）等价的实体往往具有相似的关系，2）等价的实体往往具有等价的邻居。GCN可以结合属性信息和结构信息。

一个GCN模型包含多个GCN层。第  层的输入是一个顶点特征矩阵,其中n是节点的数量，是第  层的特征数，第  层的输出是新的特征矩阵：

其中是激活函数，A是的邻接矩阵，表示图的结构信,,其中是单位矩阵。是的对角节点度矩阵，是两层间的权值矩阵。是新的一层的维度。

为了同时利用实体的结构和属性信息，在GCN的每一层中为实体设置两个向量：结构向量和属性向量.在输入层中，是随机初始化的，是实体的属性向量。令和是所有实体的结构矩阵和属性矩阵，将卷积操作重新定义为：

其中和是结构和属性对应的权值矩阵，是矩阵的连接操作，激活函数是ReLU.

下面是模型的详细描述：

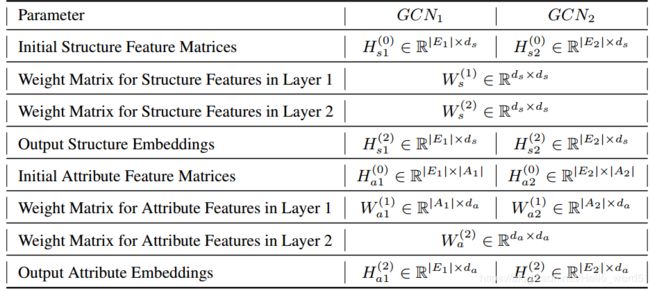
模型使用了两个两层的GCN，每个GCN处理一个KG，令分别处理KG1和KG2。对于实体的结构特征向量，将向量的维度都设置为,且两个GCN共享结构特征的权值矩阵和；对于属性嵌入，令输出特征向量的维度为.由于两个KG中属性的数量可能不同，所以两个KG的输入属性特征向量的维度可能不同。每个GCN的第一层将输入的属性特征映射为维度为的特征向量，两个模型输出的属性向量的维度相同。两个GCN的输出都是关于实体的维的嵌入，这个嵌入用于后续的实体对齐。下表列举了两个网络的参数信息。

邻接矩阵的计算：

在GCN中，连接矩阵定义了卷积计算中实体的邻居。对于一个无向图来说，可以直接使用邻接矩阵，但是KG是多关系的有向图，实体被带有类型的关系所连接。所以这里设计了计算连接矩阵的特殊方法：令表示从第 i 个实体传向第 j 个实体的对齐信息。两个实体等价的概率 很大程度上取决于它们与对齐的实体间存在的关系，所以为每个关系计算两个度量值：functionality 和inverse functionality：

为了计算实体 i 对实体 j 的影响，令

对齐预测：

实体对齐基于实体间的距离进行预测，对于实体和，它们之间的距离计算方法如下;

其中,是平衡两类嵌入重要性的超参数。

我们希望等价实体间的距离很小而不等价实体间的距离很大。对于特定的实体，计算其与G2中所有实体的距离并返回一个实体的列表做为候选对齐。这里同时计算了两个方向的对齐。

模型训练：

模型通过最小化下面基于margin的损失函数来训练：

其中是由通过随机替换一个实体得到的负对齐对。是区分正对齐对和负对齐对的间隔。两种损失分开优化。最后基于两种embedding计算实体的距离