凸优化工具包CVX快速入门
CVX工具包可以从斯坦福Boyed教授的个人主页下载http://cvxr.com/cvx/download/，也可以从我的资源中下载http://download.csdn.net/detail/herosofearth/9631094（我安装的是win64版）。安装过程十分简单，在Matlab运行cvx_setup脚本即可，无需其他任何操作。
最后命令行出现done时表示安装完成。
下面进行简单入门。
1.最小二乘法
这是一个最简单的凸优化问题，也是机器学习中的线性回归问题。最小二乘法问题是找到一个 x∈Rn 使得 ||Ax−b||2 最小，其中 A∈Rm×n 是满秩矩阵。最小二乘解为 x=(ATA)−1ATb 。普通的Matlab代码求解问题如下：
m = 16;n = 8;
A = randn(m,n);
b = randn(m,1);
x_ls = A \ b;计算结果如下：
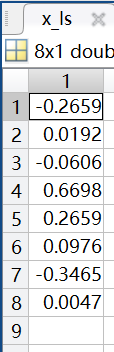
如果使用CVX工具包，同样的问题求解如下：
m = 16;n = 8;
A = randn(m,n);
b = randn(m,1);
cvx_begin
variable x(n)
minimize( norm(A*x - b) )
cvx_end可见，使用CVX的代码更加符合人类语言的阅读习惯。
- cvx_begin是创建一个新的凸优化问题的命令，在它之后就可以写出待求解的凸优化问题；
- variable x(n)定义了一个n维的变量；
- minimize( norm(A*x - b) )就是优化目标函数；
- cvx_end表示问题描述结束。
计算结果如下：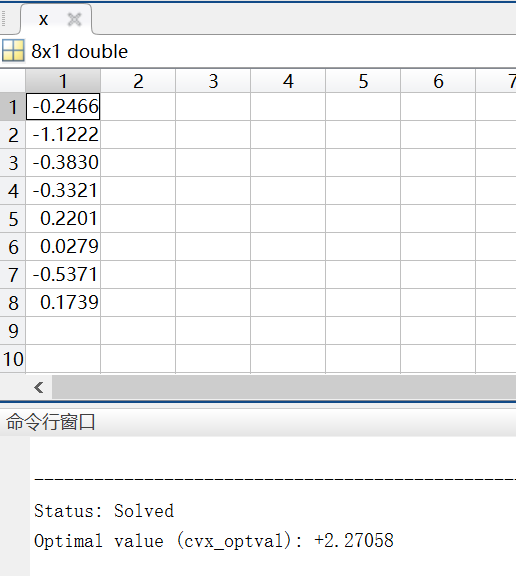
命令行窗口还会给出计算结果状态和最优值。非常人性化。
2.有约束条件的最小二乘法
假如我们希望为最小二乘问题加上上界和下界约束，问题变成：
minimize ||Ax−b||
subject to l≤x≤u
上述的 l 和 u 是给定的与x具有相同维度的向量，不等式应为广义不等式。Matlab调用二次规划的函数求解如下：
m = 16;n = 8;
A = randn(m,n);
b = randn(m,1);
bnds = randn(n,2);
l = min(bnds, [], 2);
u = max(bnds, [], 2);
x_qb = quadprog(2*A'*A, -2*A'*b, [], [], [], [], l, u);计算结果如下：
使用CVX后，代码如下：
m = 16;n = 8;
A = randn(m,n);
b = randn(m,1);
bnds = randn(n,2);
l = min(bnds, [], 2);
u = max(bnds, [], 2);
cvx_begin
variable x(n)
minimize(norm(A*x - b))
subject to
l <= x <= u
cvx_end在任何计算机编程语言中不等式都不能连着写的吧？CVX的设计应该是为了大大方便编程白痴的数学家编写代码（哈哈哈~）。计算结果如下：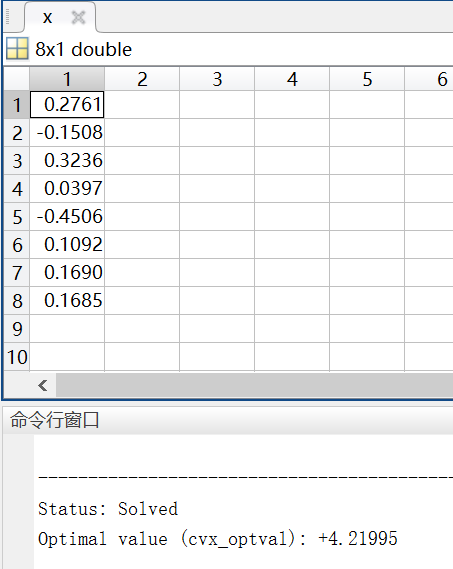
3.最优权衡曲线
这里将显示Matlab代码和CVX代码是可以混着用的。我们给目标函数加上惩罚因子 λ ，优化问题变为minimize ||Ax−b||+γ||x||1 。其中 γ 是按照对数等分的行向量。 γ 的作用是权衡原目标函数和惩罚项。下面我们作出一条最优权衡曲线，曲线由以下程序绘出：
gamma = logspace(-2,2,20);
l2norm = zeros(size(gamma));
l1norm = zeros(size(gamma));
fprintf(1,' gamma norm(x,1) norm(A*x-b)\n');
fprintf(1,'------------------------------------\n');
for k = 1:length(gamma)
fprintf(1, '%8.4e', gamma(k));
cvx_begin
variable x(n)
minimize(norm(A*x-b) + gamma(k)*norm(x,1));
cvx_end
l1norm(k) = norm(x,1);
l2norm(k) = norm(A*x - b);
fprintf(1, ' %8.4e %8.4e\n', l1norm(k), l2norm(k));
end
plot(l1norm, l2norm);
xlabel('norm(x,1)');
ylabel('norm(A*x - b)');
grid on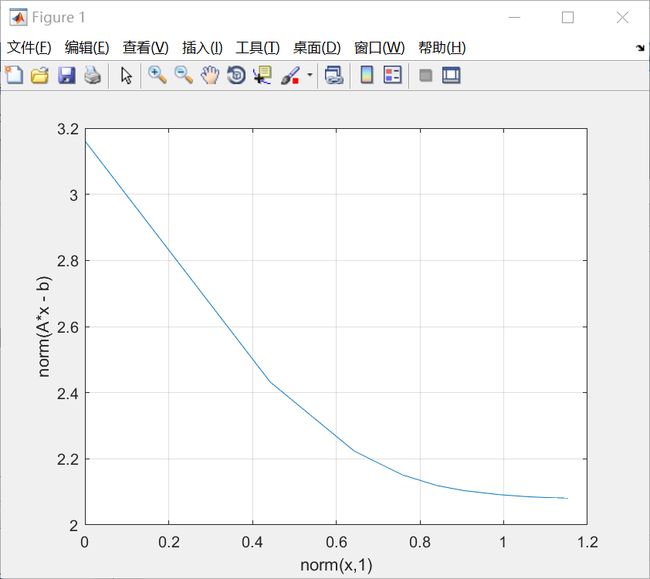
可见，当曲线收敛时， ||Ax−b||2 和 ||x||1 得到了最优权衡。
以上就是CVX的快速入门。利用好这个工具将对凸优化的学习有很大的帮助！