PAT 1135 Is It A Red-Black Tree(30 分)
There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:
- (1) Every node is either red or black.
- (2) The root is black.
- (3) Every leaf (NULL) is black.
- (4) If a node is red, then both its children are black.
- (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
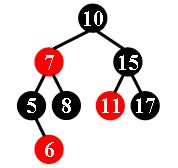
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.
 |
 |
 |
|---|---|---|
| Figure 1 | Figure 2 | Figure 3 |
For each given binary search tree, you are supposed to tell if it is a legal red-black tree.
Input Specification:
Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.
Output Specification:
For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.
Sample Input:
3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17
Sample Output:
Yes
No
No思路:统计每个节点到叶子节点的黑节点的个数用深搜
程序:
#include
#include
#include
#include
#include
using namespace std;
struct node
{
int data;
struct node *left,*right;
};
// bool cmp(int a,int b)
// {
// return abs(a) <= abs(b);
// }
// struct node* create(vector v1,vector v2,int a,int b,int c,int d)
// {
// if(a > b) return NULL;
// struct node* root = (struct node*)malloc(sizeof(struct node));
// root->data = v1[a];
// int pos = c;
// while(v2[pos] != v1[a])
// {
// pos++;
// }
// root->left = create(v1,v2,a+1,a+pos-c,c,pos-1);
// root->right = create(v1,v2,a+pos-c+1,b,pos+1,d);
// return root;
// }
void build(struct node* &root,int val)
{
if(root == NULL)
{
root = (struct node*)malloc(sizeof(struct node));
root->data = val;
root->left = NULL;
root->right = NULL;
}
else
{
if(abs(val) < abs(root->data))
build(root->left,val);
else
build(root->right,val);
}
}
void dfs(struct node* root,int temp,int &black)
{
if(root == NULL)
{
if(black == -1) black = temp;
else if(black != temp)
black = -2;
return;
}
if(black == -2) return;
if(root->data > 0) temp++;
dfs(root->left,temp,black);
dfs(root->right,temp,black);
}
bool isRedBlack(struct node* root)
{
if(root->data < 0)
return false;
else
{
queue q;
q.push(root);
while(!q.empty())
{
struct node* temp = q.front();
if(temp->left)
q.push(temp->left);
if(temp->right)
q.push(temp->right);
if(temp->data < 0)
{
if(temp->left)
{
if(temp->left->data < 0)
return false;
}
if(temp->right)
{
if(temp->right->data < 0)
return false;
}
}
int black = -1;
dfs(temp,0,black);
if(black == -2)
return false;
q.pop();
}
}
return true;
}
int main()
{
int n;
scanf("%d",&n);
for(int i = 0; i < n; i++)
{
int m;
scanf("%d",&m);
// vector v;
struct node* root = NULL;
for(int j = 0; j < m; j++)
{
int data;
scanf("%d",&data);
build(root,data);
// v.push_back(data);
}
// vector v1 = v;
// sort(v1.begin(),v1.end(),cmp);
// struct node* root = create(v,v1,0,v.size()-1,0,v1.size()-1);
if(isRedBlack(root))
printf("Yes\n");
else
printf("No\n");
}
return 0;
}