中值坐标及其应用（仅讨论图像变形与纹理参数化）

　　本文主要的参考文献为：
1. 游戏编程中的数学——调和函数和中值坐标
2. Hormann K, Floater M S. Mean value coordinates for arbitrary planar polygons[J]. Acm Transactions on Graphics, 2006, 25(4):1424-1441.
3. Floater M S. Mean value coordinates[J]. Computer Aided Geometric Design, 2003, 20(1):19-27.
　　一般来说，我们不通过一个模型含有的网格（通常为三角形网格或四边形网格）以及顶点去理解它，而是在其网格上建立一个函数，这个函数拥有特定的性质，有助于解决我们面临的难题。那么这次介绍一个在网格上建立函数的方法——中值坐标。中值坐标是90年代后期产生的，其背后的数学原理却得追述到18、19世纪了，然而直到今天它依然没有受到游戏开发界足够的重视……本文重点是谈谈中值坐标的构造与应用。

中值坐标的“前菜”

　　由 Ceva 逆定理可以很容易证明三角形 Δv1v2v3 的三条中线交于一点（重心） v ，即重心的存在性得以证明： ∃ω1,ω2,ω3∈R,s.t.

ω1v1+ω2v2+ω3v3ω1+ω2+ω3=v.

　　 Mo¨bius 在1827年将 ω1,ω2,ω3 定义为 v 的重心坐标。在实际使用时，通常会对重心坐标进行归一化。
　　这些归一化后的重心坐标在网格上是连续的，并且具有 Lagrange 性：

ωi(vj)=δij={1,i=j0,i≠j.

　　这就是为什么它们通常用于对一个三角形区域进行线性插值，并且在计算机图形学中具有广泛的应用（例如 Phong 着色，纹理映射），几何建模（例如 B 样条插值）以及许多其它领域（例如有限元方法）。
　　在许多实际应用中，将重心坐标推广到具有任意 n 边形上的插值是非常必要的。并且通常用重心坐标的下述表现形式：

∑i=1nωi(v)(vi−v)=0,

　　再将其归一化得

λi(v)=ωi(v)∑j=1nωj(v),

　　这样平面上的任一点 v 均可以写成 v1,v2,⋯,vn 在权重 ω1,ω2,⋯,ωn 下的仿射组合。而且，这些坐标应该满足 Lagrange 性：

λi(vj)=δij={1,i=j0,i≠j.

中值坐标的构造

　　令 Ψ 是平面上的一个任意简单多边形（在几何形状中，简单多边形是由直线，非相交的线段或“边”组成的扁平形状，其成对连接以形成封闭路径。 如果两边相交，那么多边形并不简单。定义参考自百度百科简单多边形），其顶点 v1,⋯,vn(n⩾3) ，其各边（互不相交）
　　

ei=(vi,vi+1)={(1−μ)vi+μvi+1:0<μ<1},i=1,⋯n−1,

　　如图所示为一些简单多边形的小栗子：

　　由上图可以看出，简单多边形可以为凹多边形，也支持嵌套操作，并不局限于单个凸多边形。
　　对于 i=1,⋯,n ，我们定义 v∈R2 到 vi 的距离：

ri(v)=||vi−v||,

　　这是通常的欧氏距离，并用 αi(v) 表示 ∠vivvi+1 。则

Ai(v)=ri(v)ri+1(v)sin(αi(v))2,Bi(v)=ri−1(v)ri+1(v)sin(αi−1(v)+αi(v))2,

　　它们分别表示 Δvvivi+1 与 Δvvi−1vi+1 的面积。各符号的直观说明可参考下图：

　　

　　易知 Ai(v),−Bi(v),Ai−1(v) 是关于 △ivi−1vivi+1 的 v 的齐次重心坐标，即

Ai(v)(vi−1−v)−Bi(v)(vi−v)+Ai−1(v)(vi+1−v)=0.(∗)

　　通常，这些坐标还需要进行归一化，即需要除以 Ci=Ai−1(v)+Ai(v)−Bi(v) 。显然这些重心坐标直接依赖于四边形 vvi−1vivi+1 的各部分面积。这是一个很棒的性质( ^▽^)！
　　现在让我们来考虑一下 v 关于所有三角形 △1,⋯,△n 的齐次重心坐标，不妨作如下定义（在后面你们便能够体会到这样的定义是多么地巧妙~）：

ωi(v)=bi−1(v)Ai−2(v)−bi(v)Bi(v)+bi+1(v)Ai+1(v),

　　其中权重函数 bi:R2→R 的选择是有一定讲究的（这个会放在后面讨论），则由(*)可以知道函数 ωi 是相应于 Ψ 的齐次重心坐标，这是因为：

∑i=1nωi(v)(vi−v)=∑i=1nbi(v)(Ai(v)(vi−1−v)−Bi(v)(vi−v)+Ai−1(v)(vi+1−v))=0.

　　欲验证上式，我们首先得解释一下当 i=1 时 v0,A0 代表的意义，以及当 i=n 时 An+1 代表的意义。其实用数据结构当中循环队列的观点去看待就很容易理解了：

　　由上图可以看出， v0 就相当于 vn ，同理可得 A0 相当于 An ， An+1 相当于 A0 。
　　现在的关键步骤是对于齐次重心坐标的归一化，必须保证 λi(v)=ωi(v)∑j=1nωj(v) 中的分母不为0。对于凸多边形这是容易实现的。
　　事实上，由 ωi(v) 的定义我们可以得到

W(v)=∑i=1nωi(v)=∑i=1nbi(v)Ci,

　　当 Ψ 是凸多边形时，所有 Ci 都有相同的符号，并且只要权重函数 bi(v) 恒正（负）， W(v) 不为0。这里权重函数 bi(v) 的恒正（负）性是比较重要的(但在后面可以看到，这个并非决定因素），举个栗子，不妨考虑 Wachspress 齐次坐标或者离散谐波坐标，它们可以由下述权重函数产生：

bWi=1Ai−1Ai,bDi=r2iAi−1Ai.

　　然而，在一个非凸多边形中， W(v) 可能取0，很重要的一个原因是此时 bi(v) 并不是恒正（负）的。于是归一化后的齐次重心坐标 λi(v) 将有可能出现间断点。
　　为了解决上述问题，通常采用的解决方案是令权重函数 bi(v) 为一个常数函数，如令 bi=1Ci ，如此一来 W≡n>0 。尽管这样一个特殊的操作能够给出一个 well−defined 的归一化齐次坐标 λi （只要 Ψ 中的任意三个顶点不共线即可），但却出现了一个致命的缺陷！！！它不满足 Lagrange 性：

λi(vj)≠δij={1,i=j0,i≠j.

　　针对上述问题， Sukumar 与 Malsch 在2005年提出了度量坐标：

bMi=1Ciqi−1qi,

　　其中 qi=ri+ri+1−||vi+1−vi|| 保证了 W(v) 不为0。其相应的归一化坐标满足 Lagrange 性，但它与离散齐次坐标类似，它们都无法保证在一个凸多边形内的取值介于0到1之间。因此，由此产生的插值函数有可能将插值点“放置”在数据集闭包的外边，这在某些应用中是不希望的。
　　现在，我们就来介绍一种最常用的重心坐标，它就是我们今天这篇文章的主角——中值坐标，其权重函数是酱紫定义的：

bMVi=riAi−1Ai

　　可能看到这里就有人感到不解了，这货长得不就跟 Wachspress 齐次坐标或者离散谐波坐标的权重函数差不多吗？为什么它们有可能使得 W=0 ，而中值坐标的权重函数就能避免这样的情况发生呢？
　　事实上，这个证明是比较复杂的，需要两个引理才能证明，篇幅较长，因此这里不再赘述。有兴趣的同学可以看看第2篇参考文献，文中的定理4.3便给出了答案。
　　继续走下去，将 bMVi 代入 ωi(v) 的定义式，得

ωi(v)=bi−1(v)Ai−2(v)−bi(v)Bi(v)+bi+1(v)Ai+1(v)=ri−1Ai−riBi+ri+1Ai−1Ai−1Ai,

　　再将 Ai(v)=ri(v)ri+1(v)sin(αi(v))2,Bi(v)=ri−1(v)ri+1(v)sin(αi−1(v)+αi(v))2 代入，同时结合一些三角函数的性质可以将 ωi 简化为

ωi=2tan(αi−1/2)+tan(αi/2)ri,

　　上式是 Floater 在2003年得到的结果。注意到这些 ωi 虽然定义在平面区域上但却具有三个分量（齐次坐标），且 ωi 只依赖于 vi 及其两个邻点 vi−1,vi+1 。这与 Wachspress 齐次坐标或者离散谐波坐标类似，但却不适用于度量坐标，因为它依赖的是 vi−2,⋯,vi+2 五个坐标点。
　　至此，离整个中值坐标的构造便仅差一步了！！！✿✿ヽ(°▽°)ノ✿

中值坐标的性质

　　对于任一简单多边形的集合 Ψ ，我们称函数 λi:R2→R,i=1,⋯,n 为中值坐标，其中

λi(v)=⎧⎩⎨⎪⎪⎪⎪⎪⎪ωi(v)/∑nj=1ωj(v), v∉Ψ,(1−μ)δi,j+μδi,j+1,v=(1−μ)vj+μvj+1∈ej,δij,v=vj

　　中值坐标具有如下优美的性质（证明都可以参见第2篇参考文献）：

• 仿射精度：对于任一仿射函数 φ:R2→Rd 都有 ∑i=1nλiφ(vi)=φ ；
• Lagrange 性： λi(vj)=δi,j ；
• 光滑性：当 v≠vj 时， λi∈C∞ ；而当 v=vj 时， λi∈C0 ；
• 正则性： ∑i=1nλi≡1 ；
• 相似不变性：如果 φ:R2→R2 是具有相似性的（此处具有相似性的变换定义为该变换是一个平移变换，旋转变换，反射变换，等距缩放变换或者它们的组合），且 Ψ^=φ(Ψ) ，则 λi(v)=λ^i(φ(v)) ；
• 线性无关性：如果 ∑i=1nciλi(v)=0,v∈R2 ，则 ci=0 ；
• 如果我们令 Ψ^ 是由 Ψ 在 ej 边上增加一点 v^=(1−μ)vj+μvj+1 ，则 λj=λ^j+λ,λj+1=λ^j+1+μλ^ ，且 λi=λ^i,i≠j,j+1 ；
• 线性性： λi 在 Ψ 的任一条边 ej 上是线性的；

• 非负性： λi 在凸多边形的内核上是正的，其中，平面上简单多边形的核是该多边形内部的一个点集，该点集中任意一点与多边形边界上一点的连线都处于这个多边形内部。譬如说，就是一个在一个房子里面放一个摄像 头，能将所有的地方监视到的放摄像头的地点的集合即为多边形的核。（参考自博客半平面交，求解多边形内核）

  至此，整个中值坐标的构造算是大功告成了！！！✿✿ヽ(°▽°)ノ✿

中值坐标的应用

　　中值坐标最主要的应用便是在给定简单多边形 Ψ 的顶点 vi 以后，对于整个多边形区域的插值。换句话说，如果 fi(v)∈Rd 是在 vi 上的插值基函数，则我们可以将函数 F:R2→Rd 定义如下：

F(v)=∑i=1nλi(v)fi(v).

　　由于 λi 的 Lagrange 性和线性性， F(vi)=f(vi) ，且 F(v) 在 Ψ 的任一条边 ej 上是线性的。
　　事实上，接下来所讨论的两个应用本质上还是体现了一种插值思想。

图像变形

　　中值坐标的一个应用是图像变形，因为中值坐标为这个问题提供了一个特别简单的解决方案，可简要地说明如下。
　　给定一个矩形区域 Ω ，一个源多边形的集合 Ψ ，其顶点 vi∈Ω ，以及一个拓扑同胚的目标多边形的集合 Ψ^ （显然 Ψ 与 Ψ^ 顶点数相同），其顶点 v^i∈Ω ，我们想构建一个平滑的变形函数 f:Ω→Ω ，它将每一个 vi 映射到相应的 v^i 。这样一个变形函数 f 可以通过令 I^=I∘f−1 将一个源图像 I:Ω→C （ C 是一个颜色空间）转换为一个目标图像 I^:Ω→C 。我们通常会令 I^=I∘f−1 而非 I^=I∘f ，这样一种思想也称为逆向映射（两者的不同其实即为正映射与逆向映射的区别，具体可以参见博客图像变换——向前映射和向后映射），等等在后面会用一些实验结果图让大家感受一下两种映射方式的不同。
　　许多时候，图像变形函数可以用 Ψ^ 的中值坐标 λ^i 去表示：

g(x)=∑i=1nλ^i(x)vi，

　　它将每一个 v^i 映射到 vi 上，如此一来便可以定义一个合适的图像变形函数。举一个不是特别恰当的例子， Shepard 提出了 IDW （ Inverse distance weighted interpolation methods ）用于图像变形，之所以说它不是很恰当，是因为 IDW 并不是严格建立在中值坐标的理论基础之上的，准确地说它是沿用了一般的重心坐标的思想，该方法要求找到满足以下形式的函数：

g(v^)=∑i=1nλi(v^)gi(v^).

　

• gi(x) 满足 gi(v^i)=vi ，这是对于点 v^i 的插值， i=1,2,⋯,n 。对于插值基函数 gi 而言，一般使用线性或者二次多项式，多项式系数可以用插值点处的导数值去确定。

• λi:R2→R 是权函数，须满足条件 λi(v^i)=1,∑i=1nλi(v^i)=1 且 λi(v^)⩾0,i=1,2,⋯,n 。
  　　 Shepard 提出了以下简单的权函数：
  

  λi(v^)=ωi(v^)∑i=1nωj(v^),
  
  　　其中 ωi(v^)=1ri ， ri 是 v^ 与 v^i 的距离。
  　　 IDW 是一种全局插值算法，即全部样本点都会参与到与某一插值结点（实际运用当中又叫控制点）的运算当中去，所以它的计算复杂度起码为 O(nN) ，其中 n 是控制点的数量， N 是整个目标图像的像素点数量。　　
  　　我们不妨来看一下分别令 I^=I∘f 与 I^=I∘g 会产生什么不同的神奇现象。（ g=f−1 ，下面直接令 gi(v^)=v^+vi−v^i ）
  　　若采用 I^=I∘f ，容易发现生成的目标图像中会出现许多空洞点（为了突出空洞点，图中用深红色点表示空洞点），如下图所示：
  
  
  
  正向映射实验效果图

  　　对于上述问题，我们需要对空洞进行填补，我分别采用了均值滤波模板、中位数滤波模板与即时填充空洞进行处理：
  

  
  
  均值滤波模板填补效果图

填补后局部放大图

　　容易看出，在对图像进行空洞区域的填补以后，出现了一些疑似空洞的点，故仍需要进行改进。先来简要分析一下原因~
　　由于存在取平均值的操作，故当一个像素点周围存在不同颜色的像素点时，填补以后容易出现颜色差异较大的点，譬如黑色方块和白色方块相邻边界上的空洞点，填补以后就会变成灰色点。
　　找到原因以后便可以有针对性地进行改进，自己采用的解决方案是替换均值滤波模板改用中位数滤波模板，需要注意的是，对一个空洞点填补时并不考虑周围的空洞点，即不应该将空洞点的像素用来求中位数；其次，若一个空洞点周围的非空洞点像素点数量为偶数时，其中位数是需要取平均的，此时容易出现类似使用均值滤波模板的填补错误，于是需要进行如下判断，假设该空洞点周围的非空洞点像素点数组为 surrounding_pixels,surrounding_pixels.size()%2==0 ：

if surrounding_pixels[i] =  = surrounding_pixels[i - 1],i=surrounding_pixels.size()/2
　　将surrounding_pixels[i]赋给空洞点;
else
　　为了避免出现取均值的操作，依然将surrounding_pixels[i]赋给空洞点;

中位数滤波模板填补效果图

　　在作了上述改进以后，发现仍存在一些问题，如：

改进填补后的局部放大图

　　可以看出，一些方块边缘会出现“毛边”现象，即方块颜色会“渗入”相邻的方块。究其原因，发现在填补时空洞点周围的空洞点太多，影响了其中位数的取值，因为对空洞点进行中位数滤波时是要舍去周围的空洞像素的，如下图所示：

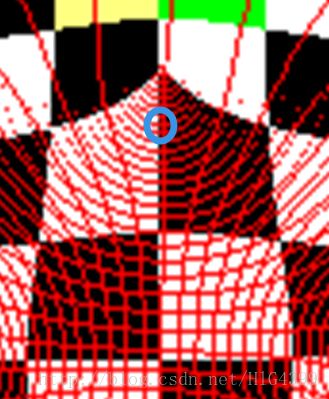
　　为了解决上述现象，需要对空洞点进行即时填补，因为在之前的程序当中，找到空洞点对其进行中位数滤波以后，出于当前填补结果若是错误会对后面的填补效果产生影响的考虑，并非直接进行填补，而是先把像素存储起来，等到最后再进行填补。
　　而现在则需要对此做出改变，只要保证当前空洞点的填补结果是正确的就可以了。自己的做法如下所示：假设该空洞点周围的非空洞点像素点数组为 surrounding_pixels,surrounding_pixels.size()%2==0 ：

if surrounding_pixels[i] =  = surrounding_pixels[i - 1],i=surrounding_pixels.size()/2
　　将surrounding_pixels[i]赋给空洞点;
else
　　先不进行操作，将这个点记录下来，等对全部点进行中值滤波以后再对这个点进行中值滤波，此时因为之前的空洞点已被填补，故它能获得更多有效的像素点;

即时填补空洞效果图

　　可以看出，在改进以后实验结果有了一定的改善。那么，我们再来看一下采用 I^=I∘g 的实验效果：

逆向映射实验效果图

　　可以看出，实验的效果十分理想。无论是在算法运行时间及算法实现难度上都远胜之前的正向映射+空洞填补算法。当然对于图像变形还有其它优秀的算法，比如径向基函数算法（ RBF 算法），限于篇幅此处不再赘述，不过可以弱弱地放张效果图让你们看看哈：

纹理参数化

　　中值坐标的另一个应用是纹理参数化，简要地说明如下。

（图片画得并不是很标准哈，见谅 (:3 」∠) ）

　　首先需要进行局部参数化：将局部结构映射到平面上，映射过程满足下列条件：

||vi−v||=||xi−x||,∠vivvi+1=2π∠xixxi+1/θ,

　　其中， θ=∑i=1d∠xixxi+1 。
　　对于点 v ，考虑多边形 v1v2⋯vn ，它存在唯一的中值坐标，不妨设其中值坐标为 (λ1,λ2,⋯,λn) ，则有 v=∑i=1nλi(v)vi,λi(vj)=δij 。
　　如此一来，我们便可以定义函数 g(v) 来进行纹理参数化：

g(v)=∑i=1nλi(v)gi(v).

　　其中， gi(vi),i=1,2,⋯,n 根据自己的需要进行设置。
　　然而，真正将上述方法用于纹理参数化的话会出现计算量太大的问题，因为它需要对模型内每一个点进行计算。因此，在实际运用当中，如果模型是比较规则的或者有足够多的顶点集，则可以弃用上述的中值坐标，改用构造一个关于顶点变换的稀疏线性系统，亦可以求出形状变化比较小的参数化结果。

原网格

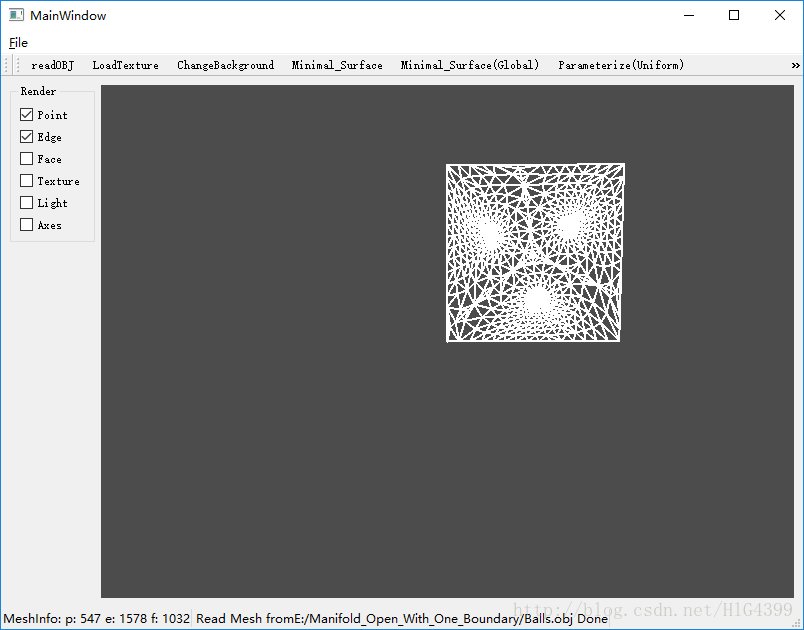
参数化结果

总结

　　我们已经表明，中值坐标将三角形重心坐标的概念推广到任意的简单多边形，甚至是这些简单多边形的集合。中值坐标具有许多很漂亮的性质（如 Lagrange 性），对于在简单多边形的插值别有用。
　　我们注意到，中值坐标在任意简单多边形的情况下并不是处处都是正的。另一方面，可能是恰恰由于这些性质，中值坐标的插值性能才能如此棒，而且在实际应用中发挥着重要作用。(๑•̀ㅂ•́)و✧文中实验的源码会上传到我的 Github 上，有兴趣的同学可以自行下载玩玩~