计算几何入门 1.4：凸包的构造——Jarvis March算法

回顾凸包构造算法：极点法、极边法和增量构造法，其复杂度分别为O(n^4)、O(n^3)和O(n^2)，效率经过优化已经大大提高了。接下来引入一种新的算法——Jarvis March，其复杂度也是O(n^2)，但是相较于增量构造在最好情况下效率是较高的。

一、选择排序

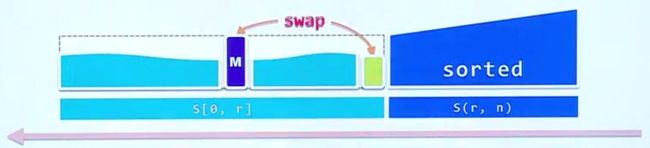
依旧是先回顾一个经典算法：选择排序（selection sort）。排序过程可以归结为下图：

对比插入排序，可以发现sorted部分变成了从后向前扩张。算法的整体思路依然是增量式的，每次选取unsorted部分中的最大元素，和sorted部分前一个元素交换，重复上述过程完成sorted部分的扩张最终使得序列有序。

 

和插入排序每次随便从unsorted部分选取元素不同，选择排序每次选取出的unsorted最大元素放在sorted前一个位置上，也就意味着整个unsorted部分必然不会超过sorted部分。从算法整体框架考虑，每次我们都是维护一个局部解（也就是sorted部分），然后从尚未处理的部分（也就是unsorted部分）找到一个与当前局部解“紧密相关的元素”（相当于选取的最大元素）。这个思想为解决凸包问题带来了新思路。

 

二、策略

再来考虑为何极边法复杂度高达O(n^3)。实际上我们要对点集中所有边进行遍历，这需要n^2复杂度，然后对每个边进行鉴别，又需要n复杂度，因此总体复杂度高达O(n^3)。那么该如何改进呢？这就可以运用选择排序的思想：将下一个要查找的边缩小到一个小范围，而非遍历所有边。

 

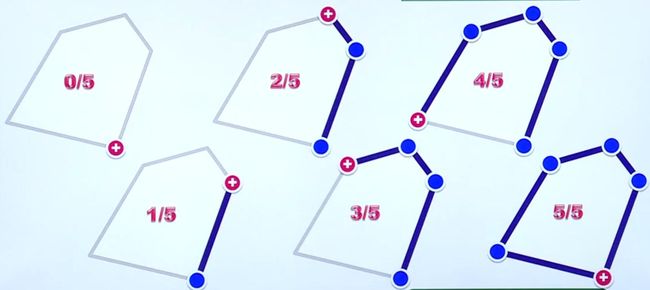
先对算法的大致过程有直观的认识（标识为：已找到极边数/所有极边数）：

 

首先从任何一个极点（后面说明如何找到这个点）开始（图中0/5），然后找到一条以这个极点为端点的极边（1/5）。接着沿着极边另一个端点（endpoint）出发，再找出下一条极边（2/5）。如此反复操作，最终会找到一条以最初极点为endpoint的极边，得到一个封闭的环，凸包也构造完成。凸包构造过程类似于选择排序中sorted不断向前扩展一样，不断扩展局部解，最后得到问题最终解。

 

凸包构造的问题由此分解为一个个子问题：如何从endpoint出发找到下一条极边。

 

 

三、继续to left test

考虑以下一般情况：

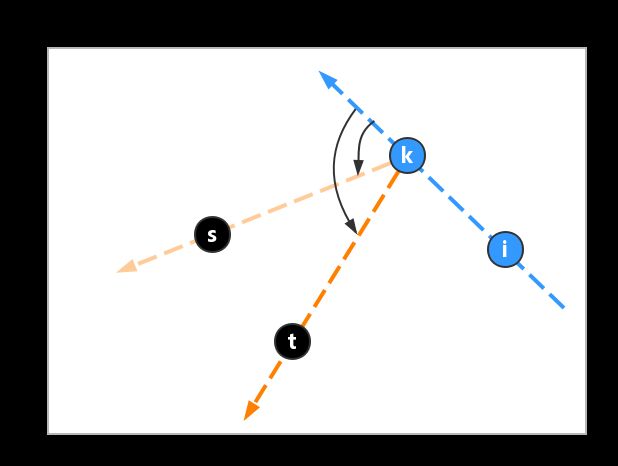
我们从极点o开始寻找极边，假设当前找到的极边是ik，接下来要做的工作是找到从k出发的另一条极边ks，即找到极点s。

 

显然，s来自于其他那些尚未处理的点中，那么s与其他点相比有什么特征？观察发现，ik作为一条极边，它的右侧肯定都是空的，所有其他点都在ik左侧。画出k与其他候选点的有向直线，例如下图中的ks，kt：

注意图中红色标出的角度，可以看出ks与ik的夹角比kt小，也就是ks比kt相较于ik偏左的角度更小。实际上ks偏左的角度比其他任何从k出发的边都小，这就是s点的判定依据。

 

这样就找到了从其余点中选择s点的思路：任选两个点，从k出发过这两点做有向边，看哪个偏左的角度更小就留下，另一点丢弃。然后再拿一点与留下的点比较，反复这个过程，最终留下的就是要找的s点。

 

问题至此转化为：如何比较两条有向边（例如ks和kt）相较于另一有向直线（例如ik）谁偏左的角度更小。

 

当然可以通过计算三角函数的方法来比较，这是最直观的数学思维。但是这样计算十分复杂，更重要的是引入了误差。这时候又要使用to left test这个基础方法来解决问题了。

具体做法就是以在ks和kr中以任意个为基准（如以ks为基准），对另一点（如t）做to left test。上图点t和有向边ks的to left test结果为true，t在ks左边，因此ks偏左的角度更小，舍弃点t。

 

类比选择排序来理解，sorted部分就相当于已得到的极边（从极点o开始到ik的首尾相连的极边），unsorted部分相当于其余点，从unsorted部分取出极大值就相当于找到点s——能构成最小偏角的点。选择排序中的选择过程需要比较元素大小，就要由一种比较器完成，而上述比较偏角的过程也可以抽象为一种比较器的操作。构造凸包的算法框架与选择排序相同，只是比较器替换为to left test而已。

 

//此处只是考虑一般情况，一些特殊细节未进行处理。例如在st上有s和s'两点，这两点的取舍问题未考虑。当然为了理解算法整体框架忽略特殊情况是很必要的。

 

然后考虑一个细节问题，也就是上文提到的算法最开始第一个极点如何确定。任何一个极点都可以使用，我们没必要去计算出哪个点是极点。可以选取y坐标最小的点，也就是最低点，在没有退化的情况下，这个点一定是一个极点。如果情况退化，有多个最低点（如例图中所示），我们就去选x坐标最小的那个点，也就是最左边的点即可。这种方法选出的点称为lowest-then-leftmost point（LTL）。注意选取的规则的先后顺序，先选lowest，若点不唯一再选leftmost。

四、Jarvis March

类比选择排序的过程，我们得到的凸包构造算法就是Jarvis March算法，又称gift wrapping算法（算法过程如包装礼物一样）。接下来看算法具体实现方法。

bool ToLeft(Point p, Point q, Point s)
{
	int area2 =   p.x * q.y - p.y * q.x 
				+ q.x * s.y - q.y * s.x
				+ s.x * p.y - s.y * p.x;
	
	return area2 > 0;	//左侧为真
}

int ltl(Point S[], int n)
{
	int LTL = 0;
	for (int k = 1; k < n; k++)
		if (S[k].y < S[LTL].y ||
			(S[k].y == S[LTL].y &&
			 S[k].x < S[LTL].x))
			LTL = K;
	return LTL;
}

void Jarvis(Point S[], int n)
{
	for (int = 0; k < n; k++)
		S[k].extreme = false;	//首先将所有点标记为非极点
	
	int LTL = ltl(s, n);	//找到LTL
	int k = LTL;			//将LTL作为第一个极点
	
	do
	{
		S[k].extreme = true;	//判定为极点
		int s = -1;
		
		//选取下一个极点，每次比较两个点s和t，
		//做点t和有向边ks的to left test，最终找到s
		for (int t = 0; t < n; t++)
			if (t != k && t != s &&	//除了k和s外每个点
				(s == -1 || !ToLeft(P[k], P[s], P[t]))) // 
				s = t;	//如果t在s右边
		
		S[k].succ = s;	//k点的后继为s
		k = s;	//s变为下一次查找的起点
	} while (LTL != k)
}

最后分析Jarvis March算法相较于增量构造法的优势。二者都是O(n^2)的复杂度，Jarvis March算法的优势在于其的“输出敏感性（output sensitive）”。考虑点集S，共有n个点，来构造S上的凸包。

 

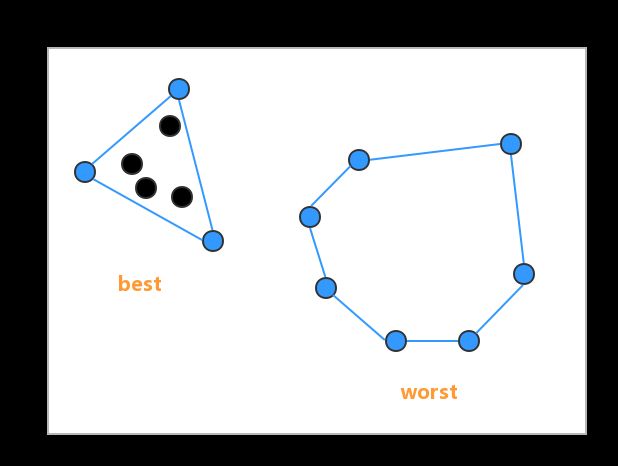
何为“输出敏感性”？Jarvis March算法每次新加入一条边都会耗费n的复杂度，但是构造过程一共会加入的边数往往比n少。如下图（设n = 7）：

在非退化为共线的前提下，最好情况为只加入3条边（复杂度为O(3n)），最坏情况为所有点都是极点，加入n-1条边（复杂度为O(n^2)）。实际情况中最坏情况出现的几率很小，我们引入一个指标h来衡量凸包的极边数（the size of convex hull）：

h = |CH(S)|

Jarvis March算法算法的复杂度更准确的表示为O(nh)。h又由最终输出结果，即凸包本身来决定，输出结果决定了构造过程的复杂度，这就是所谓的“输出敏感性”。这种类型的算法又被称为output sensitive algorithm。这种特性在其它凸包算法中也会体现。

 

本文是学堂在线课程《计算几何》的笔记，帮助理解和记录思考过程，不够严谨请见谅。