Torch7入门续集（五）----进一步了解optim

总说

现在看以前写的入门续集，觉得写的好烂，但我不想改了。在torch7学习（六）稍微提到了optim，觉得写的很不清楚，所以有了这篇。
入门续集到了这篇，个人认为看Torch框架的深度学习代码应该没啥大问题了。

总览

x*, {f}, ... = optim.method(opfunc, x[, config][, state])

• opfunc: 自定义的闭包，必须包含:我们计算的f 对于优化的参数x的求导的API，比如大部分我们是训练网络，然后我们的 f 就是loss，而x就是网络的weight。此时我们在opfunc中必须包含”API”, 这个“API”在这里类似是：

-- 这里的loss就是f
local loss = criterion:forward(predict, trainlabels)
local dloss_dpredict = criterion:backward(predict,trainlabels)

-- 这里调用backward，这个backward会计算gradWeight, gradBias以及gradInput.
local gradInput = net:backward(trainset, dloss_dpredict)

• x: 需要优化的参数，这里的x必须是一维的！
• config: 根据不同的优化方法，设置不同的选项。
• state: 这个一般包含learningRate，learningRateDecay之类的。
• x*: 其中 x* = argmin_x f(x)
• {f}: 略

一般的写法：

require 'optim'

local optimState = {learningRate = 0.01}

local params, gramParams = net:getParameters()

function feval(params)
-- 无论如何，在f函数中，先要将需要“优化的参数的梯度”设置成0
   gradParams:zero()

-- 重新计算“需要优化的参数”。
   local outputs = model:forward(batchInputs)
   local loss = criterion:forward(outputs, batchLabels)
   local dloss_doutputs = criterion:backward(outputs, batchLabels)
   model:backward(batchInputs, dloss_doutputs)

-- 返回f值，就是loss，以及gramParams(这个必须是一维的)
   return loss, gradParams
end

for epoch = 1, 50 do

   -- 加载点数据，干点额外的事。

   -- 在最后一句调用optim.method
   optim.sgd(feval, params, optimState)
end

再次强调:backward只是调用每一层的 updateGradInput以及accGradParameters，并不会更新参数，只是计算参数的梯度，以及计算每一层的输入的梯度。

local fDx = function(x)
    netD:apply(function(m) if torch.type(m):find('Convolution') then m.bias:zero() end end)
    netG:apply(function(m) if torch.type(m):find('Convolution') then m.bias:zero() end end)

    gradParametersD:zero()

    -- Real
    -- train netD with (real, real_label)
    local output = netD:forward(real_AB)
    local label = torch.FloatTensor(output:size()):fill(real_label)
    if opt.gpu>0 then 
        label = label:cuda()
    end

    local errD_real = criterion:forward(output, label)
    local df_do = criterion:backward(output, label)
    -- 这里对针对real的图，计算netD的网络的输入的梯度，以及网络参数的梯度。
    netD:backward(real_AB, df_do)  

    -- Fake
    -- train netD with (fake_AB, fake_label)
    local output = netD:forward(fake_AB)
    label:fill(fake_label)
    local errD_fake = criterion:forward(output, label)
    local df_do = criterion:backward(output, label)
    -- 这里的netD的参数没有置0，所以梯度是累加！
    -- 当netD经过real和fake的计算后，梯度“中和”后，再将我们需要优化
    -- 的网络的参数的梯度 gradParametersD输出。
    netD:backward(fake_AB, df_do)

    errD = (errD_real + errD_fake)/2

    return errD, gradParametersD
end

可以结合 Torch7入门续集（八）—终结篇的“再次说说网络更新权值的方式”来理解。

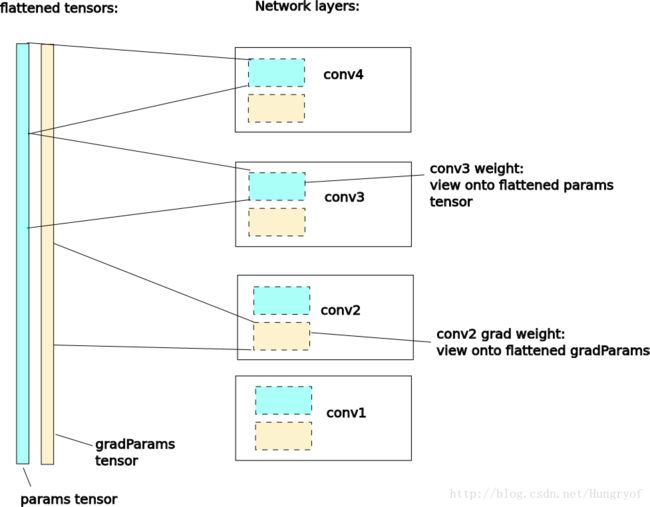
getParameters

我们发现，上面采用了getParameters函数。这个函数会将网络中的参数全部压缩成一维的存储空间连续的Tensor。并返回网络中的weight（以及bias）和gradWeight(以及gradBias）。
前面提到optim.method要求需要优化的参数x必须是一维的！

两种典型的训练写法

方式一：针对网络参数的训练（大部分情况）

这种就是训练一个模型呗，优化weight，使之能够完成特定任务。比如VGG之类的。

local parametersD, gradParametersD = netD:getParameters()

-- 自定义闭包
local fDx = function(x)

    gradParametersD:zero()

    local output = netD:forward(real_AB)
    local label = torch.FloatTensor(output:size()):fill(real_label)

    local errD_real = criterion:forward(output, label)
    local df_do = criterion:backward(output, label)
    netD:backward(real_AB, df_do)

    errD = errD_real

    return errD, gradParametersD
end

然后在训练时

for epoch = 1, opt.niter do
    for i = 1, math.min(data:size(), opt.ntrain), opt.batchSize do

        -- load a batch and run G on that batch
        createRealFake()

        optim.adam(fDx, parametersD, optimStateD)


        -- 做点其他的事情
     end  

    parametersD, gradParametersD = netD:getParameters() -- reflatten the params and get them
    collectgarbage()
end

方式一的分析

然后我们要优化的是netD的参数，那么我们必须
1. 先确认我们需要优化的参数，好了，我们需要优化的是D网络的参数，所以肯定要让netD进行一次backward。
2. 显然我们要先得到loss，才能进行backward。所以我们要将netD:forward，得到loss后，再反向传播得到dLoss_doutput
3. dLoss_doutput用backward经过netD。值得注意的是，调用backward前，必须先进行该网络的forward。

local fDx = function(x)
-- 第一步，先让需要优化的参数的梯度为0.
-- 一万年不变，这句话。
    gradParametersD:zero()


-- 中间部分。这里无论怎么写，必须至少要包含我们参数所在的网络的一次backward。
    local output = netD:forward(real_AB)
    local label = torch.FloatTensor(output:size()):fill(real_label)

    local errD_real = criterion:forward(output, label)
    local df_do = criterion:backward(output, label)
    netD:backward(real_AB, df_do)

    errD = errD_real

 -- 这里返回的 gradParametersD 是由getParameters()返回的，已经是被压平成1维的了。
    return errD, gradParametersD
end

下面这种是常规写法。adam或是sgd等等都是这种方式，必须指定迭代的次数！

for epoch = 1, opt.niter do
    for i = 1, math.min(data:size(), opt.ntrain), opt.batchSize do

        -- load a batch and run G on that batch
        createRealFake()

        optim.adam(fDx, parametersD, optimStateD)


        -- 做点其他的事情
     end  

-- 最后要重新获得参数，毕竟是用for循环的。   
    parametersD, gradParametersD = netD:getParameters() -- reflatten the params and get them
    collectgarbage()
end

方式二：针对输入的训练（不改变模型的参数，只不断改变输入）

这种一般是通过迭代的方式，使得输入能满足某种分布，从而使得loss最小。一般采用已有的模型。比如neural style中的采用VGG19模型，它并不改变模型的参数，而是不断改变input。也就是说，我们这里需要优化的参数是gradInput!
说明时，采用neural_style的代码。

  local num_calls = 0
  local function feval(x)
    num_calls = num_calls + 1
    -- net:forward(x)会让content_module以及style_module各层计算loss
    net:forward(x)
    -- 由于并没有groundtruth的图。所以直接dy赋值为全是0的tensor
    local grad = net:updateGradInput(x, dy)
    -- loss包括content层的以及style层的，然后让这些loss加起来，让loss最小即可。
    local loss = 0
    for _, mod in ipairs(content_losses) do
      loss = loss + mod.loss
    end
    for _, mod in ipairs(style_losses) do
      loss = loss + mod.loss
    end
    maybe_print(num_calls, loss)
    maybe_save(num_calls)

    collectgarbage()
    -- 返回的第一个参数是loss，是要最小化的目标，而传入feval的参数是要优化的参数。
    -- optim.lbfgs expects a vector for gradients
    return loss, grad:view(grad:nElement())
  end

训练时：

  -- Run optimization.
  if params.optimizer == 'lbfgs' then
    print('Running optimization with L-BFGS')
    local x, losses = optim.lbfgs(feval, img, optim_state)
  elseif params.optimizer == 'adam' then
    print('Running optimization with ADAM')
    for t = 1, params.num_iterations do
      local x, losses = optim.adam(feval, img, optim_state)
    end
  end

方式二: 分析

由于这种并不更新网络的参数，所以就不要 gradParams:zero() 了。
更新输入时，由于这里没有groundtruth。我们只是希望 G(F(in)) 与 G(F(S)) 差异最小，同时希望 F(in) 和 F(C) 最小。这里的local grad = net:updateGradInput(x, dy)为什么可以这样做。 以styleLoss的updateInput为例。对于最后一层的style层，gradOutput是值为0的tensor。然后乘以strength后，直接加入gradInput。这样，最后的grad就是融合了每个层的grad的累加。

 function StyleLoss:updateGradInput(input, gradOutput)
  local dG = self.crit:backward(self.G, self.target)
  dG:div(input:nElement())
  self.gradInput = self.gram:backward(input, dG)
  if self.normalize then
    self.gradInput:div(torch.norm(self.gradInput, 1) + 1e-8)
  end
  self.gradInput:mul(self.strength)
  self.gradInput:add(gradOutput)
  return self.gradInput
end

训练时当遇到lbfgs，这个函数会不断调用feval，所以就不需要放入for中了。

  -- Run optimization.
  if params.optimizer == 'lbfgs' then
    print('Running optimization with L-BFGS')
    local x, losses = optim.lbfgs(feval, img, optim_state)
  elseif params.optimizer == 'adam' then
    print('Running optimization with ADAM')
    for t = 1, params.num_iterations do
      local x, losses = optim.adam(feval, img, optim_state)
    end
  end