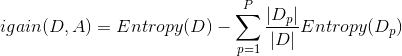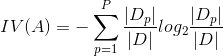随机森林 RF 算法的原理（一）

随机森林算法是一种重要的基于 Bagging 的集成学习方法，可用来做分类、回归等问题。随机森林算法是由一系列的决策树组成，他通过自助法（Bootstrap）重采样技术，从原始训练样本集中有放回的重复随机抽取 m 个样本，生成新的训练样本集合，然后根据自主样本集生成 k 个分类树组成随机森林，新数据的分类结果按分类树投票多少形成的分数定。其实质是对决策树算法的一种改进，将多个决策树合并在一起，每棵树的建立依赖于一个独立抽取得样本，森林中的每棵树具有相同的分布，分类误差取决于每一棵树的分类能力和它们之间的相关性。

要了解随机森林，先要了解集成学习和决策树。

一、集成学习

处理前面复杂的分类问题，我们试图寻找一个高效的算法处理，但通常会花费很多资源。集成学习是训练多个分类器，利用这些分类器来解决同一个问题。相当与“三个臭皮匠赛过一个诸葛亮”（哈哈哈，我看到这的时候憋不住了，哈哈哈哈）。

集成学习：通过构建并结合多个学习器来完成学习任务，有时称为多分类器系统，其结构如下图所示。

先产生一组个体学习器，在利用某种策略将其结合起来，个体学习器通常由一个现有的学习算法从训练数据产生，例如C4.5决策树算法、BP神经网络算法等。这些集成中只包含同种类型的个体学习器，即同质，同质集成中的个体学习器亦称基学习器，相应的学习算法称为基学习算法。集成中也可以包含不同类型的个体学习器，这时相应的学习算法不再是基学习算法。要获得好的集成，个体学习器至少不差于弱学习器（指泛化性能略优于随机猜测的学习器），即学习器不能太坏、要有多样性、学习器之间具有差距。在集成学习方法中，其泛化能力比单个学习算法的强，所以集成学习的很多理论研究都是针对弱学习器进行的。根据多个分类器学习方式的不同，可以分成并行生成的 Bagging 算法和串行生成的 Boosting 算法。

集成学习有如下的特点： 
（1）将多个分类方法聚集在一起，以提高分类的准确率，聚集的算法可以是不同，也可以相同；
（2）集成学习法由训练数据构建一组基分类器，然后通过对每个基分类器的预测进行投票来进行分类； 
（3）集成学习不算一种分类器，而是一种分类器结合的方法； 
（4）通常一个集成分类器的分类性能会好于单个分类器； 
（5）如果把单个分类器比作一个决策者的话，集成学习的方法就相当于多个决策者共同进行一项决策。

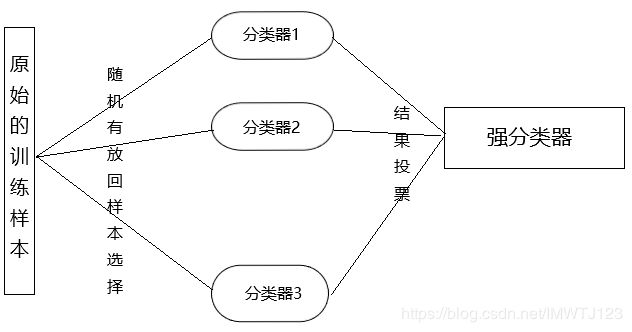
Bagging 算法：它的特点是各个弱学习器之间没有依赖关系，可以并行拟合，随机森林算法就基于 Bagging 算法。该算法是通过对训练样本随机有放回的抽取，产生多个训练数据的子集，并在每一个训练记得子集上训练一个分类器，最终的分类结果是由多个分类器的分类结果投票产生。训练一个Bagging 集成与直接使用基学习算法训练一个学习器的复杂度同阶，这说明Bagging 是一个很高效的集成学习算法。Bagging算法主要关注降低方差，因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效果更为明显。

为什么要有放回的抽取？

为获得好的集成，我们希望个体学习器不能太差，如果采样出的每个子集都完全不同，则每个基学习器只能用到一小部分训练数据，甚至不足以进行有效学习，无法确保产生出比较好的基学习器，为解决这个问题使用相互有交叠的采样子集。

所以通过m次有放回的随机采样操作，如我们得到含m个样本的采样集，初始训练集中有的样本在采样集多次出现，下有的则从未出现，初始训练集中约有63.2%的样本出现在采样集中。然后基于每个采样集训练出一个基学习器，所再将这些基学习器结合，这就是Bagging 的基本流程，图下图所示。

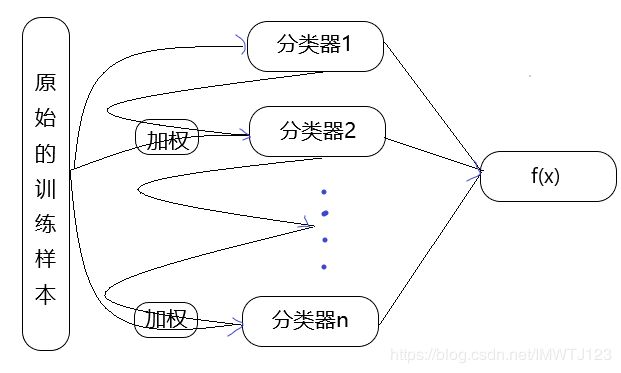
Boosting 算法：是一族可将弱学习器提升为强学习器的算法。它是通过顺序的给训练集中的数据项重新加权创造不同的基础学习器，先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器。根据每次训练集之中每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练，最后将每次训练得到的分类器最后融合起来，作为最后的决策分类器。Boosting 算法有很多版本，目前使用最广泛的是 AdaBoost  算法和 GBDT 算法。Boosting 算法主要关注降低偏差，因此Boosting 算法能基于泛化性能相当弱的学习器构建出很强的集成。如下图Boosting 算法的整个过程：

二、决策树

决策树算法是一种常用的机器学习算法，在分类问题中，决策树算法通过样本中某一维属性的值，将样本划分到不同的类别中。决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。

决策树学习也是资料探勘中一个普通的方法，每个决策树可以依靠对源数据库的分割进行数据测试。这个过程可以递归式的对树进行修剪。 当不能再进行分割或一个单独的类可以被应用于某一分支时，递归过程就完成了。另外，随机森林分类器将许多决策树结合起来以提升分类的正确率。

1.在决策树算法中，有以下标准：信息增益、增益率和基尼指数。

信息增益：对于给定的数据集，划分前后信息熵的减少量称为信息增益，即

其中Entropy（D）表示数据集D的信息熵， 表示的是属于第p类的样本的个数。

当把样本划分为两个独立的子数据集D1和D2时，信息熵为：

信息熵表示的数据集中的不纯度，信息熵较小表明数据集纯度提升。

增益率：作为选择最优化分属性的方法，计算方法：

其中IV（A）称为特征A的固有值，

基尼指数：也可以选择最优的划分属性，在数据集D中，假设有K个分类，则样本属于第k个类的概率为pk。则计算方法：

2.数据划分停止的标准

• 节点中的样本数小于给定阈值；
• 样本集中的基尼指数小于给定阈值（样本基本属于同一类）；
• 没有更多特征。

3.CART分类树算法

决策树模型主要有ID3算法，C4.5算法和CART算法。其中CART算法与ID3算法，C4.5算法不同的是它能处理分类问题也能处理回归问题。

在CART分类树算法中，利用Gini指数作为划分标准，通过样本中的特征，对样本进行划分，直到所有的叶节点中的所有样本都为同一类为止。

CART分类树构建过程：

1. 计算现有特征对该数据集的基尼指数，对于每一个特征A，可以对样本点A是否为a可以将数据集D分成数据集D1,D2；
2. 对于所有的特征A和所有可能的切分点a，选择基尼指数最小的特征以及相对应的切分点作为最优特征和最佳切分点。 
3. 对最优子树递归调用1.2到满足停止条件。 
4. 生成CART分类树。 

下面就CART算法在python中试试：
 

# -*- coding: utf-8 -*-
"""
Created on Thu Mar 14 10:37:24 2019

@author: 2018061801
"""
#cart_train.py
import numpy as np
import pickle as pk
class node:
    '''树的节点的类
    '''
    def __init__(self, fea=-1, value=None, results=None, right=None, left=None):
        self.fea = fea  # 用于切分数据集的属性的列索引值
        self.value = value  # 设置划分的值
        self.results = results  # 存储叶节点的值
        self.right = right  # 右子树
        self.left = left  # 左子树
        
def load_data(data_file):
    '''导入训练数据
    input:  data_file(string):保存训练数据的文件
    output: data(list):训练数据
    '''
    data = []
    f = open(data_file)
    for line in f.readlines():
        sample = []
        lines = line.strip().split("\t")
        for x in lines:
            sample.append(float(x))  # 转换成float格式
        data.append(sample)
    f.close()  
    return data  
     
def split_tree(data, fea, value):
    '''根据特征fea中的值value将数据集data划分成左右子树
    input:  data(list):训练样本
            fea(float):需要划分的特征index
            value(float):指定的划分的值
    output: (set_1, set_2)(tuple):左右子树的聚合
    '''
    set_1 = []  # 右子树的集合
    set_2 = []  # 左子树的集合
    for x in data:
        if x[fea] >= value:
            set_1.append(x)
        else:
            set_2.append(x)
    return (set_1, set_2)

def leaf(dataSet):
    '''计算叶节点的值
    input:  dataSet(list):训练样本
    output: np.mean(data[:, -1])(float):均值
    '''
    data = np.mat(dataSet)
    return np.mean(data[:, -1])

def err_cnt(dataSet):
    '''回归树的划分指标
    input:  dataSet(list):训练数据
    output: m*s^2(float):总方差
    '''
    data = np.mat(dataSet)
    return np.var(data[:, -1]) * np.shape(data)[0]

def build_tree(data, min_sample, min_err):
    '''构建树
    input:  data(list):训练样本
            min_sample(int):叶子节点中最少的样本数
            min_err(float):最小的error
    output: node:树的根结点
    '''
    # 构建决策树，函数返回该决策树的根节点
    if len(data) <= min_sample:
        return node(results=leaf(data)) 

    # 1、初始化
    best_err = err_cnt(data)
    bestCriteria = None  # 存储最佳切分属性以及最佳切分点
    bestSets = None  # 存储切分后的两个数据集
    # 2、开始构建CART回归树
    feature_num = len(data[0]) - 1
    for fea in range(0, feature_num):
      feature_values = {}
      for sample in data:
            feature_values[sample[fea]] = 1
      for value in feature_values.keys():
           # 2.1、尝试划分
            (set_1, set_2) = split_tree(data, fea, value)
            if len(set_1) < 2 or len(set_2) < 2:
                continue
            # 2.2、计算划分后的error值
            now_err = err_cnt(set_1) + err_cnt(set_2)
            # 2.3、更新最优划分
            if now_err < best_err and len(set_1) > 0 and len(set_2) > 0:
                best_err = now_err
                bestCriteria = (fea, value)
                bestSets = (set_1, set_2)

    # 3、判断划分是否结束
    if best_err > min_err:
        right = build_tree(bestSets[0], min_sample, min_err)
        left = build_tree(bestSets[1], min_sample, min_err)
        return node(fea=bestCriteria[0], value=bestCriteria[1], \
                    right=right, left=left)
    else:
        return node(results=leaf(data))  # 返回当前的类别标签作为最终的类别标       

def predict(sample, tree):
    '''对每一个样本sample进行预测
    input:  sample(list):样本
            tree:训练好的CART回归树模型
    output: results(float):预测值
    '''
    # 1、只是树根
    if tree.results != None:
        return tree.results
    else:
    # 2、有左右子树
        val_sample = sample[tree.fea]  # fea处的值
        branch = None
        # 2.1、选择右子树
        if val_sample >= tree.value:
            branch = tree.right
        # 2.2、选择左子树
        else:
            branch = tree.left
        return predict(sample, branch) 

def cal_error(data, tree):
    ''' 评估CART回归树模型
    input:  data(list):
            tree:训练好的CART回归树模型
    output: err/m(float):均方误差
    '''
    m = len(data)  # 样本的个数   
    n = len(data[0]) - 1  # 样本中特征的个数
    err = 0.0
    for i in range(m):
        tmp = []
        for j in range(n):
            tmp.append(data[i][j])
        pre = predict(tmp, tree)  # 对样本计算其预测值
        # 计算残差
        err += (data[i][-1] - pre) * (data[i][-1] - pre)
    return err / m

def save_model(regression_tree, result_file):
    '''将训练好的CART回归树模型保存到本地
    input:  regression_tree:回归树模型
            result_file(string):文件名
    '''
    with open(result_file, 'wb+') as f:
        pk.dump(regression_tree, f)

if __name__ == "__main__":
    # 1、导入训练数据
    print ("----------- 1、load data -------------")
    data = load_data("D:/anaconda4.3/spyder_work/sine.txt")
    # 2、构建CART树
    print ("----------- 2、build CART ------------")
    regression_tree = build_tree(data, 30, 0.3)
    # 3、评估CART树
    print ("----------- 3、cal err -------------")
    err = cal_error(data, regression_tree)
    print ("\t--------- err : ", err)
    # 4、保存最终的CART模型
    print ("----------- 4、save result -----------")  
    save_model(regression_tree, "regression_tree")

 

#rain.txt
0.190350	0.878049
0.306657	-0.109413
0.017568	0.030917
0.122328	0.951109
0.076274	0.774632
0.614127	-0.250042
0.220722	0.807741
0.089430	0.840491
0.278817	0.342210
0.520287	-0.950301
0.726976	0.852224
0.180485	1.141859
0.801524	1.012061
0.474273	-1.311226
0.345116	-0.319911
0.981951	-0.374203
0.127349	1.039361
0.757120	1.040152
0.345419	-0.429760
0.314532	-0.075762
0.250828	0.657169
0.431255	-0.905443
0.386669	-0.508875
0.143794	0.844105
0.470839	-0.951757
0.093065	0.785034
0.205377	0.715400
0.083329	0.853025
0.243475	0.699252
0.062389	0.567589
0.764116	0.834931
0.018287	0.199875
0.973603	-0.359748
0.458826	-1.113178
0.511200	-1.082561
0.712587	0.615108
0.464745	-0.835752
0.984328	-0.332495
0.414291	-0.808822
0.799551	1.072052
0.499037	-0.924499
0.966757	-0.191643
0.756594	0.991844
0.444938	-0.969528
0.410167	-0.773426
0.532335	-0.631770
0.343909	-0.313313
0.854302	0.719307
0.846882	0.916509
0.740758	1.009525
0.150668	0.832433
0.177606	0.893017
0.445289	-0.898242
0.734653	0.787282
0.559488	-0.663482
0.232311	0.499122
0.934435	-0.121533
0.219089	0.823206
0.636525	0.053113
0.307605	0.027500
0.713198	0.693978
0.116343	1.242458
0.680737	0.368910
0.484730	-0.891940
0.929408	0.234913
0.008507	0.103505
0.872161	0.816191
0.755530	0.985723
0.620671	0.026417
0.472260	-0.967451
0.257488	0.630100
0.130654	1.025693
0.512333	-0.884296
0.747710	0.849468
0.669948	0.413745
0.644856	0.253455
0.894206	0.482933
0.820471	0.899981
0.790796	0.922645
0.010729	0.032106
0.846777	0.768675
0.349175	-0.322929
0.453662	-0.957712
0.624017	-0.169913
0.211074	0.869840
0.062555	0.607180
0.739709	0.859793
0.985896	-0.433632
0.782088	0.976380
0.642561	0.147023
0.779007	0.913765
0.185631	1.021408
0.525250	-0.706217
0.236802	0.564723
0.440958	-0.993781
0.397580	-0.708189
0.823146	0.860086
0.370173	-0.649231
0.791675	1.162927
0.456647	-0.956843
0.113350	0.850107
0.351074	-0.306095
0.182684	0.825728
0.914034	0.305636
0.751486	0.898875
0.216572	0.974637
0.013273	0.062439
0.469726	-1.226188
0.060676	0.599451
0.776310	0.902315
0.061648	0.464446
0.714077	0.947507
0.559264	-0.715111
0.121876	0.791703
0.330586	-0.165819
0.662909	0.379236
0.785142	0.967030
0.161352	0.979553
0.985215	-0.317699
0.457734	-0.890725
0.171574	0.963749
0.334277	-0.266228
0.501065	-0.910313
0.988736	-0.476222
0.659242	0.218365
0.359861	-0.338734
0.790434	0.843387
0.462458	-0.911647
0.823012	0.813427
0.594668	-0.603016
0.498207	-0.878847
0.574882	-0.419598
0.570048	-0.442087
0.331570	-0.347567
0.195407	0.822284
0.814327	0.974355
0.641925	0.073217
0.238778	0.657767
0.400138	-0.715598
0.670479	0.469662
0.069076	0.680958
0.294373	0.145767
0.025628	0.179822
0.697772	0.506253
0.729626	0.786514
0.293071	0.259997
0.531802	-1.095833
0.487338	-1.034481
0.215780	0.933506
0.625818	0.103845
0.179389	0.892237
0.192552	0.915516
0.671661	0.330361
0.952391	-0.060263
0.795133	0.945157
0.950494	-0.071855
0.194894	1.000860
0.351460	-0.227946
0.863456	0.648456
0.945221	-0.045667
0.779840	0.979954
0.996606	-0.450501
0.632184	-0.036506
0.790898	0.994890
0.022503	0.386394
0.318983	-0.152749
0.369633	-0.423960
0.157300	0.962858
0.153223	0.882873
0.360068	-0.653742
0.433917	-0.872498
0.133461	0.879002
0.757252	1.123667
0.309391	-0.102064
0.195586	0.925339
0.240259	0.689117
0.340591	-0.455040
0.243436	0.415760
0.612755	-0.180844
0.089407	0.723702
0.469695	-0.987859
0.943560	-0.097303
0.177241	0.918082
0.317756	-0.222902
0.515337	-0.733668
0.344773	-0.256893
0.537029	-0.797272
0.626878	0.048719
0.208940	0.836531
0.470697	-1.080283
0.054448	0.624676
0.109230	0.816921
0.158325	1.044485
0.976650	-0.309060
0.643441	0.267336
0.215841	1.018817
0.905337	0.409871
0.154354	0.920009
0.947922	-0.112378
0.201391	0.768894

结果：

----------- 1、load data -------------
----------- 2、build CART ------------
----------- 3、cal err -------------
        --------- err :  0.017472201263739866
----------- 4、save result -----------

 下节将讲随机森林及其实践

 

 

参考文献：赵志勇《python 机器学习算法》

周志华《机器学习》