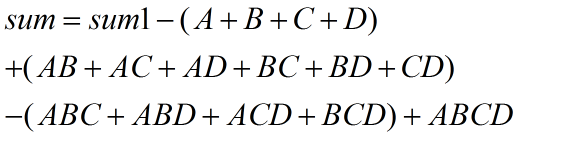奋斗的demon——基本计数方法（实践二）

 

之前demon要学车，还参加了一个组队赛，一时没有更新，抱歉。

demon继续大白老师作业：1个容斥原理题目（拉拉队）

1个二项式系数题目（超级平均数）

【例2 拉拉队】（容斥原理）

　　In most professional sporting events, cheerleaders play a major role in entertaining the spectators. Their
roles are substantial during breaks and prior to start of play. The world cup soccer is no exception.
Usually the cheerleaders form a group and perform at the centre of the field. In addition to this group,
some of them are placed outside the side line so they are closer to the spectators. The organizers would
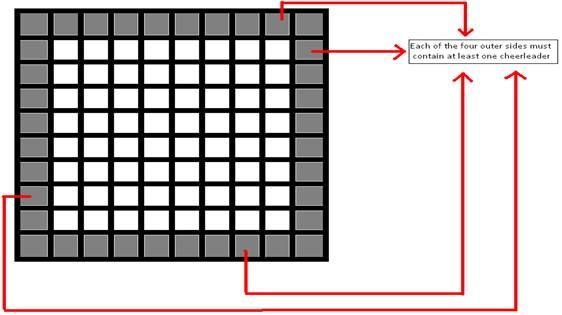
like to ensure that at least one cheerleader is located on each of the four sides. For this problem, we
will model the playing ground as an M × N rectangular grid. The constraints for placing cheerleaders
are described below:
• There should be at least one cheerleader on each of the four sides. Note that, placing a cheerleader
on a corner cell would cover two sides simultaneously.
• There can be at most one cheerleader in a cell.
• All the cheerleaders available must be assigned to a cell. That is, none of them can be left out.
The organizers would like to know, how many ways they can place the cheerleaders while maintaining
the above constraints. Two placements are different, if there is at least one cell which contains a
cheerleader in one of the placement but not in the other.

Input
The first line of input contains a positive integer T ≤ 50, which denotes the number of test cases. T
lines then follow each describing one test case. Each case consists of three nonnegative integers, 2 ≤ M,
N ≤ 20 and K ≤ 500. Here M is the number of rows and N is the number of columns in the grid. K
denotes the number of cheerleaders that must be assigned to the cells in the grid.
Output
For each case of input, there will be one line of output. It will first contain the case number followed by
the number of ways to place the cheerleaders as described earlier. Look at the sample output for exact
formatting. Note that, the numbers can be arbitrarily large. Therefore you must output the answers
modulo 1000007.
Sample Input
2
2 2 1
2 3 2
Sample Output
Case 1: 0
Case 2: 2

[题解]

这个问题我们可以抽象的看做在m行n列的矩形中放入k个石头，问有多少种方法？题目要求是”第一行、最后一行、第一列、最后一列都得有石头“的方法数。

假设我们遇到得问题是这样的，要求”第一行、最后一行、第一列、最后一列都没有有石头“，这样我们可能会很容易的写出答案，C((m-2)(n-2),k)。但是这道题我们可以利用容斥原理，把问题转化成上面这种问题。

设满足”满足第一行没有石头“的集合为A,最后一行没有石头的集合为B，第一列没有石头的集合为C，最后一列没有石头的集合为D，全集为S，则问题转化为在S中但不在A，B，C，D任何一个集合中的元素的个数。则利用容斥原理，我们可以得出

                              

【例3 超级平均数】（二项式系数）                            

 

Do you know how to compute the mean (or average) of n numbers? Well, that's not good enough for me. I want the supermean! "What's a supermean," you ask? I'll tell you. List the n given numbers in non-decreasing order. Now compute the average of each pair of adjacent numbers. This will give you n - 1 numbers listed in non-decreasing order. Repeat this process on the new list of numbers until you are left with just one number - the supermean. I tried writing a program to do this, but it's too slow. :-( Can you help me?

Input
The first line of input gives the number of cases, N. N test cases follow. Each one starts with a line containing n (0<n<=50000). The next line will contain the ninput numbers, each one  between -1000 and 1000, in non-decreasing order.

Output
For each test case, output one line containing "Case #x:" followed by the supermean, rounded to 3 fractional digits.

Sample Input

4

1

10.4

2

1.0 2.2

3

1 2 3

5

1 2 3 4 5

Sample Output

Case #1: 10.400

Case #2: 1.600

Case #3: 2.000

Case #4: 3.000

[题目解析] 给出n(n≤50000)个数，每相邻两个数求平均数，将得到n-1个数。这n-1个数每相邻两个数求平均数，将得到n-2个数。以此类推，最后得到1个数。求这个数。

1.这道题首先想到是是杨辉三角，每个数字被选取的次数就是杨辉三角中的系数，那么每个数字对最后就是C(n-1,k)*A[k]/(2^n-1),将全部数字带入累加就是最后结果。

2.题目的范围a(0<n≤50000),吃不消，但是可以取对数：e^(lnC(n-1,k)*A[k]/(2^n-1))=>e^(lnC(n-1,k)+lnA[k]-(n-1)*ln2);

3.C(n,k)=C(n,k-1)*(n-k+1)/k;(性质4，详见 奋斗的demon——基本计数方法（理论）)，依次类推。

#include 
#include 
#include 
#include 
using namespace std;
int n;
double value;
int main()
{

    int caseNum, num = 1;
    cin>>caseNum;
    while(caseNum--)
    {
        cin>>n;
        n = n-1;
        double ln2 = n*log(2), lnc = 0;
        double ans = 0.0;
        cin>>value;
        if(value > 0) ans += exp( log(value)+lnc-ln2 );
        else ans -= exp( log(-value)+lnc-ln2 );
        for(int i = 1; i <= n; ++i)
        {
            cin>>value;
            lnc += log(n-i+1)-log(i);
            if(value > 0) ans += exp( log(value)+lnc-ln2 );
            else ans -= exp( log(-value)+lnc-ln2 );
        }
        cout<<"Case #"<